[集训]dance

题意

http://uoj.ac/problem/77

 

思考

显然能转化为最小割模型。若没有pi的代价，则对于第i个格子，可以让源点连向第i个点，容量为黑色收益，再连向汇点，容量为白色收益。再考虑pi的代价，对1~n的每个点新建一个哨兵节点，并向它连容量为pi的边。若前面存在点j落在当前区间中，再将哨兵节点连向点j，容量为正无穷。

但这样边数达到O(n^2)级别，不能接受。

发现哨兵节点所连的边对于ai来说都是一个连续的区间，可用主席树优化建图，边数将为O(nlogn)级别。

 

代码

  1 #pragma GCC optimize 2
  2 #include<bits/stdc++.h>
  3 using namespace std;
  4 typedef long long int ll;
  5 const ll inf=INT_MAX;
  6 int n;
  7 int head[5005*80+233],size=1;
  8 int dfn[5005*80],S,T;
  9 int what[5005],tmp[5005],Last[5005];
 10 ll valBoy[5005],valGirl[5005],a[5005],l[5005],r[5005],p[5005];
 11 struct edge
 12 {
 13     int to,next;
 14     ll w;
 15 }E[5005*80+233];
 16 inline ll max(ll x,ll y)
 17 {
 18     return x>y?x:y;
 19 }
 20 inline ll min(ll x,ll y)
 21 {
 22     return x<y?x:y;
 23 }
 24 inline void addEdge(int u,int v,ll w)
 25 {
 26     E[++size].to=v;
 27     E[size].next=head[u];
 28     E[size].w=w;
 29     head[u]=size;
 30 }
 31 inline void add(int u,int v,ll w)
 32 {
 33     addEdge(u,v,w);
 34     addEdge(v,u,0);
 35 }
 36 bool bfs()
 37 {
 38     memset(dfn,-1,sizeof(dfn));
 39     queue<int>Q;
 40     Q.push(S);
 41     dfn[S]=0;
 42     while(!Q.empty())
 43     {
 44         int u=Q.front();
 45         Q.pop();
 46         for(int i=head[u];i;i=E[i].next)
 47         {
 48             int v=E[i].to;
 49             if(dfn[v]!=-1||E[i].w==0)
 50                 continue;
 51             dfn[v]=dfn[u]+1;
 52             Q.push(v);
 53         }
 54     }
 55     return dfn[T]!=-1;
 56 }
 57 ll dinic(int u,ll up)
 58 {
 59     if(u==T)
 60         return up;
 61     ll sum=0;
 62     for(int i=head[u];i;i=E[i].next)
 63     {
 64         int v=E[i].to;
 65         if(dfn[v]!=dfn[u]+1||E[i].w==0)
 66             continue;
 67         ll g=dinic(v,min(E[i].w,up-sum));
 68         E[i].w-=g;
 69         E[i^1].w+=g;
 70         sum+=g;
 71         if(g==0)
 72             dfn[v]=-1;
 73         if(sum==up)
 74             break;
 75     }
 76     return sum;
 77 }
 78 struct czyTree
 79 {
 80     int t[5005*80],cur,root[5005],son[5005*80][2];
 81     int tot;
 82     void addPos(int pos,int l,int r,int&num,int pre,int from)
 83     {
 84         num=++tot;
 85         son[num][0]=son[pre][0],son[num][1]=son[pre][1];
 86         if(l==r)
 87         {
 88             add(num+T,from,inf);
 89             if(Last[pos])
 90                 add(num+T,Last[pos]+T,inf);
 91             Last[pos]=num;
 92             return;
 93         }
 94         int mid=(l+r)>>1;
 95         if(pos<=mid)
 96             addPos(pos,l,mid,son[num][0],son[pre][0],from);
 97         else
 98             addPos(pos,mid+1,r,son[num][1],son[pre][1],from);
 99         if(son[num][0])
100             add(num+T,son[num][0]+T,inf);
101         if(son[num][1])
102             add(num+T,son[num][1]+T,inf);
103     }
104     void addS(int L,int R,int l,int r,int num,int from)
105     {
106         if(!num)
107             return;
108         if(L<=l&&r<=R)
109         {
110             add(from,num+T,inf);
111             return;
112         }
113         int mid=(l+r)>>1;
114         if(R<=mid)
115             addS(L,R,l,mid,son[num][0],from);
116         else if(mid<L)
117             addS(L,R,mid+1,r,son[num][1],from);
118         else
119             addS(L,R,l,mid,son[num][0],from),addS(L,R,mid+1,r,son[num][1],from);
120     }
121 }Tree;
122 int main()
123 {
124     ios::sync_with_stdio(false);
125     cin>>n;
126     int tot=0;
127     for(int i=1;i<=n;++i)
128     {
129         cin>>a[i]>>valBoy[i]>>valGirl[i]>>l[i]>>r[i]>>p[i];
130         tmp[++tot]=a[i];
131     }
132     sort(tmp+1,tmp+tot+1);
133 //    tot=unique(tmp+1,tmp+tot+1)-tmp-1;
134     S=0,T=2*n+1;
135     for(int i=1;i<=n;++i)
136     {
137         add(S,i,valBoy[i]);
138         add(i,T,valGirl[i]);
139         add(i,i+n,p[i]);
140     }
141     for(int i=1;i<=n;++i)
142     {
143         int L=1,R=tot;
144         while(tmp[L]<l[i]&&L<=tot)
145             ++L;
146         while(r[i]<tmp[R]&&R)
147             --R;
148         Tree.addS(L,R,1,tot,Tree.root[i-1],i+n);
149         Tree.addPos(lower_bound(tmp+1,tmp+tot+1,a[i])-tmp,1,tot,Tree.root[i],Tree.root[i-1],i);
150     }
151     ll ans=0;
152     while(bfs())
153         ans+=dinic(S,inf);
154     for(int i=1;i<=n;++i)
155         ans-=valBoy[i]+valGirl[i];
156     cout<<-ans<<endl;
157     return 0;
158 }
View Code

 

细节

如下图所示，若此题使用dinic，左右两个建图方式是不等价的，且左图是正确的，右图是错误的，并且右图的最小割结果会变小。（假设有很多蓝色边）

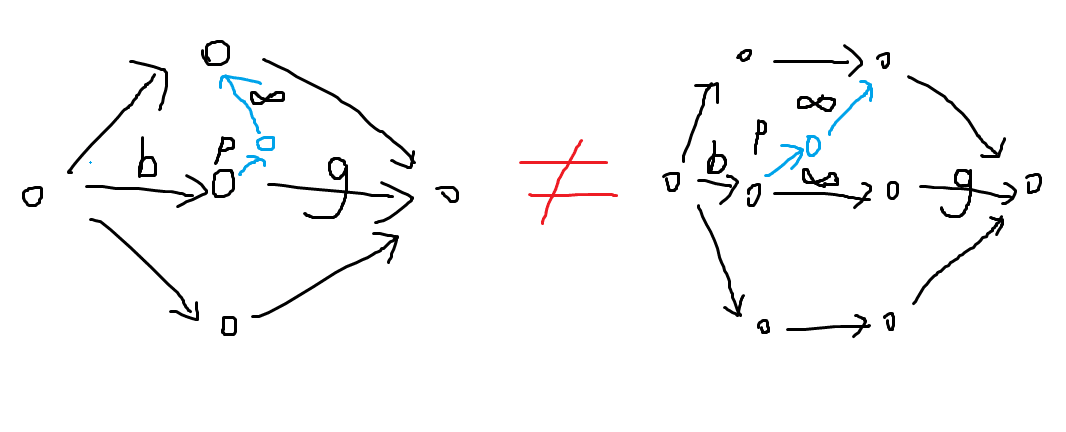
事实上，哨兵节点连出的边必须连在左边一排点上。

考虑下图所示情况。在dinic中，若先走了红色路径，则无法经过蓝色路径。原因是蓝色正无穷边此时不存在反向边，蓝色路径不连通。这样，最小割就少了一些流量。

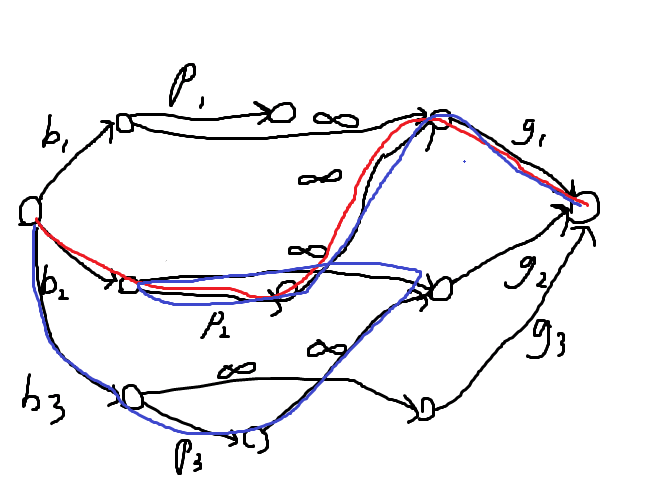
此外，在主席树建图中，要注意相同ai的点要连向前一个相同ai的点。

(CORRECTED BY CZY)

 posted on 2019-07-05 06:55  GreenDuck  阅读(200)  评论(0)  编辑  收藏  举报