[模板]计算几何模板

1.声明

1.博主比较菜，只会二维。还只会OI常用的。

2.不要吐槽换行。

3.精度、圆周率：

1 const ld eps=1E-10;
2 const ld pi=acos(-1);
3 const ld inf=1E9;
View Code
有时要long double，有时要int。
4.正确判相等：
1 inline bool equal(double x,double y)
2 {
3     return abs(x-y)<=eps;
4 }
View Code

 

2.单元操作

1.点类：

 1 struct pt
 2 {
 3     ld x,y;
 4     int id;
 5     pt(ld a=0,ld b=0,int c=0){x=a,y=b,id=c;}
 6     pt operator+(const pt&A){return pt(x+A.x,y+A.y);}
 7     pt operator-(const pt&A){return pt(x-A.x,y-A.y);}
 8     pt operator*(ld d){return pt(x*d,y*d);}
 9     pt operator/(ld d){return pt(x/d,y/d);}
10     ld operator*(const pt&A){return x*A.y-y*A.x;}
11     inline ld len()//返回长度 
12     {
13         return sqrt(x*x+y*y);
14     }
15     inline ld angle()//返回弧度 
16     {
17         return atan2(y,x);
18     }
19     void out(){cout<<"("<<x<<","<<y<<")";}
20 };
View Code

2.线类：

1 struct line
2 {
3     pt A,B;
4     line(pt x=pt(),pt y=pt())
5     {
6         A=x,B=y;
7     }
8 };
View Code

3.圆类：

 1 struct circle
 2 {
 3     pt O;
 4     ld r;
 5     circle(pt A=pt(),ld b=0):O(A),r(b){}
 6     inline pt get(ld ra)//得到圆上的某个点 
 7     {
 8         return pt(O.x+cos(ra)*r,O.y+sin(ra)*r);
 9     }
10 };
View Code

4.判断方向的叉积，代表了以OB为参考，OA关于OB的方向。返回值为1代表OA在OB的顺时针方向上，-1代表逆时针，0代表共线：

1 inline int cross(pt A,pt B)
2 {
3     double d=A*B;
4     if(equal(d,0))
5         return 0;
6     else if(d>eps)
7         return 1;
8     return -1;
9 }
View Code

5.两点之间的距离：

1 inline double s(double x)
2 {
3     return x*x;
4 }
5 inline double dis(pt A,pt B)
6 {
7     return sqrt(s(A.x-B.x)+s(A.y-B.y));
8 }
View Code
6.两条直线的交点：
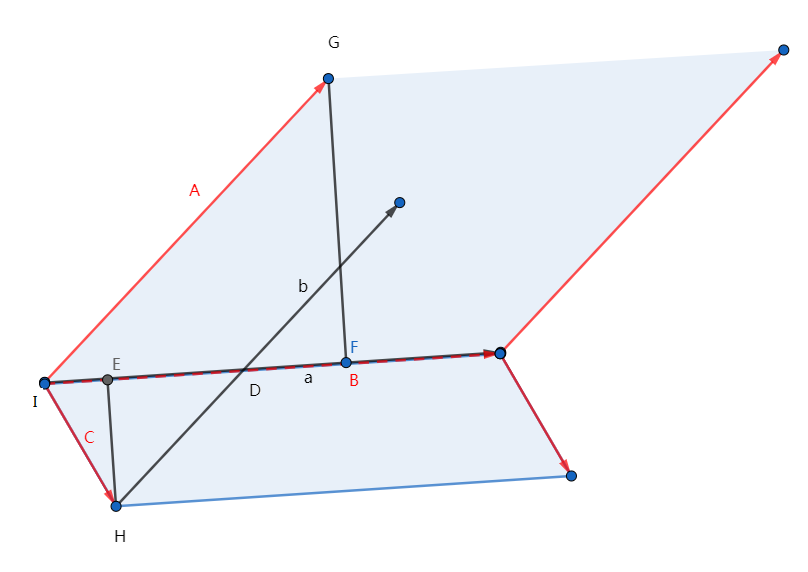
我们设求的是向量a和向量b的交点（图中有箭头，黑色实线的，a被红色的挡住了一部分）。我们先算出A=b终点-b起点，B=a终点-a起点，C=b起点-a起点，再将他们三个的起点拼到一起，移到a的起点（这只是图上的表述，实现不需要移动），ABC为左边标红的向量，中间一条为虚线。
我们在算出B叉A，C叉B，得到两个有向的平行四边形的面积，如图中蓝色部分。
再从H和G向a向量引垂线，得到垂足E和F。得到相似三角形DEH和IFG。此时平行四边形的面积比即为相似比。
这样我们可以得到HD与|A|的相似比（就是平行四边形面积比），将向量b乘上该相似比加到H上即可。
1 inline pt intersection(line a,line b)
2 {
3     pt A=b.B-b.A,B=a.B-a.A,C=b.A-a.A;
4     if(cross(A,B)==0)
5         return pt(inf,inf);
6     double d=-(B*C)/(B*A);
7     return b.A+A*d;
8 }
View Code

7.将A绕B逆时针旋转ra（弧度制，误差巨大）：

1 inline pt rotate(pt A,pt B,double ra)
2 {
3     double x=A.x-B.x,y=A.y-B.y;
4     return pt(B.x+x*cos(ra)-y*sin(ra),B.y+x*sin(ra)+y*cos(ra));
5 }
View Code

8.垂足：

1 inline pt foot(pt A,line a)
2 {
3     return intersection(line(A,A+pt(a.B.y-a.A.y,a.A.x-a.B.x)),a);
4 }
View Code

 9.跨立实验：

1 inline bool seg(line a,line b)
2 {
3     return cross(a.A-b.A,b.B-b.A)*cross(a.B-b.A,b.B-b.A)==-1&&
4            cross(b.A-a.A,a.B-a.A)*cross(b.B-a.A,a.B-a.A)==-1;
5 }
View Code

 10.圆的公切线：

 1 inline int GCCI(circle A,circle B,vector<line>&wait)
 2 {
 3     int cnt=0;
 4     if(A.r<B.r)
 5         swap(A,B);
 6     pt u=B.O-A.O;
 7     ld d=u.len(),rD=A.r-B.r,rA=A.r+B.r;
 8     cout<<d<<' '<<rD<<' '<<rA<<endl; 
 9     if(d-rD<0)//内含 
10         return 0;
11     if(abs(d)<=eps&&abs(A.r-B.r)<=eps)//重合 
12         return -1;
13     ld base=u.angle();
14     if(abs(d-rD)<=eps)//内切,有些许爆精度的风险 
15     {
16         cnt+=2;
17         wait.push_back(line(A.get(base),B.get(base+(1E-9))));
18         return cnt;
19     }
20     ld da=acos((A.r-B.r)/d);
21     cnt+=2;//外公切线 
22     wait.push_back(line(A.get(base+da),B.get(base+da)));
23     wait.push_back(line(A.get(base-da),B.get(base-da)));
24     if(abs(d-rA)<=eps)//1内公切线,有些许爆精度的风险 
25     {
26         cnt+=1;
27         wait.push_back(line(A.get(base),B.get(base+pi+(1E-9))));
28     }
29     else if(d-rA>eps)//2内公切线 
30     {
31         da=acos((A.r+B.r)/d);
32         cnt+=2;
33         wait.push_back(line(A.get(base+da),B.get(base+da+pi)));
34         wait.push_back(line(A.get(base-da),B.get(base-da+pi)));
35     }
36     return cnt;
37 }
View Code

 

 

3.算法

1.极角排序求凸包：

 1 pt O(0,0);
 2 bool cmp(pt A,pt B)
 3 {
 4     double x=atan2(A.y-O.y,A.x-O.x),y=atan2(B.y-O.y,B.x-O.x);
 5     if(equal(x,y))
 6         return dis(A,O)<dis(B,O);
 7     return x<y;
 8 }
 9 vector<pt>convex(vector<pt>P)
10 {
11     int pos=0;
12     for(int i=1;i<P.size();++i)
13         if(P[i].x<P[pos].x)
14             pos=i;
15     swap(P[pos],P[0]);
16     O=P[0];
17     sort(P.begin()+1,P.end(),cmp);
18     vector<pt>ans;
19     int now=0;
20     for(int i=0;i<P.size();++i)
21     {
22         while(now>1&&cross(P[i]-ans[now-2],ans[now-1]-ans[now-2])!=-1)
23             ans.pop_back(),--now;
24         ans.push_back(P[i]);
25         ++now;
26     }
27     return ans;
28 }
View Code

 

2.半平面交

这份代码只适用于最后答案不会是一条直线、一个点、一组平行线的情况。并且取的是每个向量逆时针方向上的半平面的交。而且使静态的。

先极角排序，每次插入一条直线相当于判断这样的情况：

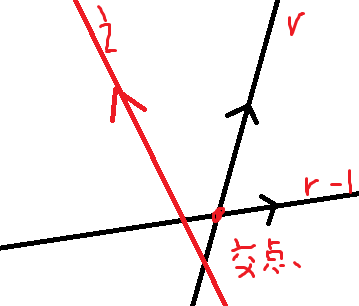
若存在，弹出r。做完后对l进行同样的操作。

加入所有直线后也要更新答案，防止冗余的直线的出现。具体看代码。

 1 inline bool cmpLine(line a,line b)
 2 {
 3     return atan2(a.A.y-a.B.y,a.A.x-a.B.x)<atan2(b.A.y-b.B.y,b.A.x-b.B.x);
 4 }
 5 inline bool onClockwise(line a,line b,line c)//b,c的交点在a顺时针方向 
 6 {
 7     return cross(intersection(b,c)-a.A,a.B-a.A)==1;
 8 }
 9 inline bool isSame(line a,line b)
10 {
11     return cross(a.A-b.B,b.A-b.B)==0;
12 }
13 line wait[66666];
14 vector<line>halfPlane(vector<line>A)
15 {
16     vector<line>ans;
17     sort(A.begin(),A.end(),cmpLine);
18     int l=1,r=0;
19     for(int i=0;i<A.size();++i)
20     {
21         while(l<r&&!isSame(A[i],wait[r])&&onClockwise(A[i],wait[r-1],wait[r]))
22             --r;
23         while(l<r&&!isSame(A[i],wait[l])&&onClockwise(A[i],wait[l],wait[l+1]))
24             ++l;
25         if(!isSame(A[i],wait[r])||r==0)
26             wait[++r]=A[i];
27         else if(!onClockwise(wait[r],wait[r-1],A[i]))
28             wait[r]=A[i];
29     }
30     while(l<r&&onClockwise(wait[l],wait[r],wait[r-1]))
31         --r;
32     while(l<r&&onClockwise(wait[r],wait[l],wait[l+1]))
33         ++l;
34     for(int i=l;i<=r;++i)
35         ans.push_back(wait[i]);
36     return ans;
37 }
View Code

 

3.平面图转对偶图：不多讲了，前面有。

这份代码只适用于所有面都联通的情况（包括用线段连起来的）。

 1 const int maxn=55555;
 2 pt P[maxn],waitP[maxn];
 3 bool visEdge[maxn*2],visP[maxn];
 4 int nextEdge[maxn*2],bel[maxn*2];
 5 struct edge
 6 {
 7     int to,next;
 8 };
 9 struct graph//size从2开始 
10 {
11     edge E[maxn*2];
12     int size,cnt,head[maxn*2];
13     graph()
14     {
15         size=1;
16     }
17     inline void add(int u,int v)
18     {
19         E[++size].to=v;
20         E[size].next=head[u];
21         head[u]=size;
22     }
23     void getEdge(int u)
24     {
25         O=P[u];
26         int tot=0;
27         for(int i=head[u];i;i=E[i].next)
28         {
29             int v=E[i].to;
30             waitP[++tot]=P[v];
31             waitP[tot].id=i;
32         }
33         sort(waitP+1,waitP+tot+1,cmp);
34         for(int i=1;i<tot;++i)
35             nextEdge[waitP[i].id]=waitP[i+1].id;
36         nextEdge[waitP[tot].id]=waitP[1].id;
37     }
38     void init()
39     {
40         for(int i=2;i<=size;++i)
41             if(!visP[E[i].to])
42             {
43                 visP[E[i].to]=1;
44                 getEdge(E[i].to);
45             }
46     }
47     void dfs(int u,int id,int color)
48     {
49         bel[id]=color;
50         visEdge[id]=1;
51         if(visEdge[nextEdge[id^1]])
52             return;
53         dfs(E[nextEdge[id^1]].to,nextEdge[id^1],color);
54     }
55     void convert(graph&G)
56     {
57         map<pair<int,int>,bool>vis;
58         init();
59         for(int i=2;i<=size;++i)
60             if(!visEdge[i])
61                 dfs(E[i].to,i,++cnt);
62         for(int i=2;i<=size;++i)
63             if(bel[i]!=bel[i^1]&&!vis[make_pair(bel[i],bel[i^1])])
64             {
65                 vis[make_pair(bel[i],bel[i^1])]=1;
66                 G.add(bel[i],bel[i^1]);
67             }
68     }
69 }G,L;
View Code

 

4.完整代码

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 typedef long double ld;
  4 const ld eps=1E-16;
  5 const ld pi=acos(-1);
  6 const ld inf=1E9;
  7 inline bool equal(ld x,ld y)
  8 {
  9     return abs(x-y)<=eps;
 10 }
 11 struct pt
 12 {
 13     ld x,y;
 14     int id;
 15     pt(ld a=0,ld b=0,int c=0){x=a,y=b,id=c;}
 16     pt operator+(const pt&A){return pt(x+A.x,y+A.y);}
 17     pt operator-(const pt&A){return pt(x-A.x,y-A.y);}
 18     pt operator*(ld d){return pt(x*d,y*d);}
 19     pt operator/(ld d){return pt(x/d,y/d);}
 20     ld operator*(const pt&A){return x*A.y-y*A.x;}
 21     void out(){cout<<"("<<x<<","<<y<<")";}
 22 };
 23 struct line
 24 {
 25     pt A,B;
 26     line(pt a=pt(),pt b=pt())
 27     {
 28         A=a,B=b;
 29     }
 30 };
 31 inline int cross(pt A,pt B)
 32 {
 33     ld d=A*B;
 34     if(equal(d,0))
 35         return 0;
 36     return d>0?1:-1;
 37 }
 38 inline ld dis(pt A,pt B)
 39 {
 40     return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
 41 }
 42 inline pt intersection(line a,line b)
 43 {
 44     pt A=b.B-b.A,B=a.B-a.A,C=b.A-a.A;
 45     if(cross(A,B)==0)
 46         return pt(inf,inf);
 47     ld d=-(B*C)/(B*A);
 48     return b.A+A*d;
 49 }
 50 inline pt foot(pt A,line a)
 51 {
 52     return intersection(line(A,A+pt(a.B.y-a.A.y,a.A.x-a.B.x)),a);
 53 }
 54 inline bool seg(line a,line b)
 55 {
 56     return cross(a.A-b.A,b.B-b.A)*cross(a.B-b.A,b.B-b.A)==-1&&
 57            cross(b.A-a.A,a.B-a.A)*cross(b.B-a.A,a.B-a.A)==-1;
 58 }
 59 pt O(0,0);
 60 bool cmp(pt A,pt B)
 61 {
 62     ld x=atan2(A.y-O.y,A.x-O.x),y=atan2(B.y-O.y,B.x-O.x);
 63     if(equal(x,y))
 64         return dis(A,O)<dis(B,O);
 65     return x<y;
 66 }
 67 vector<pt>convex(vector<pt>P)
 68 {
 69     int pos=0;
 70     for(int i=1;i<P.size();++i)
 71         if(P[i].x<P[pos].x)
 72             pos=i;
 73     swap(P[pos],P[0]);
 74     O=P[0];
 75     sort(P.begin()+1,P.end(),cmp);
 76     vector<pt>ans;
 77     int now=0;
 78     for(int i=0;i<P.size();++i)
 79     {
 80         while(now>1&&cross(P[i]-ans[now-2],ans[now-1]-ans[now-2])!=-1)
 81             ans.pop_back(),--now;
 82         ans.push_back(P[i]);
 83         ++now;
 84     }
 85     return ans;
 86 }
 87 inline bool cmpLine(line a,line b)
 88 {
 89     return atan2(a.A.y-a.B.y,a.A.x-a.B.x)<atan2(b.A.y-b.B.y,b.A.x-b.B.x);
 90 }
 91 inline bool onClockwise(line a,line b,line c)//b,c的交点在a顺时针方向 
 92 {
 93     return cross(intersection(b,c)-a.A,a.B-a.A)==1;
 94 }
 95 inline bool isSame(line a,line b)
 96 {
 97     return cross(a.A-b.B,b.A-b.B)==0;
 98 }
 99 line wait[66666];
100 vector<line>halfPlane(vector<line>A)
101 {
102     vector<line>ans;
103     sort(A.begin(),A.end(),cmpLine);
104     int l=1,r=0;
105     for(int i=0;i<A.size();++i)
106     {
107         while(l<r&&!isSame(A[i],wait[r])&&onClockwise(A[i],wait[r-1],wait[r]))
108             --r;
109         while(l<r&&!isSame(A[i],wait[l])&&onClockwise(A[i],wait[l],wait[l+1]))
110             ++l;
111         if(!isSame(A[i],wait[r])||r==0)
112             wait[++r]=A[i];
113         else if(!onClockwise(wait[r],wait[r-1],A[i]))
114             wait[r]=A[i];
115     }
116     while(l<r&&onClockwise(wait[l],wait[r],wait[r-1]))
117         --r;
118     while(l<r&&onClockwise(wait[r],wait[l],wait[l+1]))
119         ++l;
120     for(int i=l;i<=r;++i)
121         ans.push_back(wait[i]);
122     return ans;
123 }
124 inline ld length(vector<pt>P)
125 {
126     ld sum=0;
127     for(int i=1;i<P.size();++i)
128         sum+=dis(P[i-1],P[i]);
129     sum+=dis(P[P.size()-1],P[0]);
130     return sum;
131 }
132 //////////////////////////////////////////////////////////////////////////////////////////////
133 const int maxn=55555;
134 pt P[maxn],waitP[maxn];
135 bool visEdge[maxn*2],visP[maxn];
136 int nextEdge[maxn*2],bel[maxn*2];
137 struct edge
138 {
139     int to,next;
140 };
141 struct graph//size从2开始 
142 {
143     edge E[maxn*2];
144     int size,cnt,head[maxn*2];
145     graph()
146     {
147         size=1;
148     }
149     inline void add(int u,int v)
150     {
151         E[++size].to=v;
152         E[size].next=head[u];
153         head[u]=size;
154     }
155     void getEdge(int u)
156     {
157         O=P[u];
158         int tot=0;
159         for(int i=head[u];i;i=E[i].next)
160         {
161             int v=E[i].to;
162             waitP[++tot]=P[v];
163             waitP[tot].id=i;
164         }
165         sort(waitP+1,waitP+tot+1,cmp);
166         for(int i=1;i<tot;++i)
167             nextEdge[waitP[i].id]=waitP[i+1].id;
168         nextEdge[waitP[tot].id]=waitP[1].id;
169     }
170     void init()
171     {
172         for(int i=2;i<=size;++i)
173             if(!visP[E[i].to])
174             {
175                 visP[E[i].to]=1;
176                 getEdge(E[i].to);
177             }
178     }
179     void dfs(int u,int id,int color)
180     {
181         bel[id]=color;
182         visEdge[id]=1;
183         if(visEdge[nextEdge[id^1]])
184             return;
185         dfs(E[nextEdge[id^1]].to,nextEdge[id^1],color);
186     }
187     void convert(graph&G)
188     {
189         map<pair<int,int>,bool>vis;
190         init();
191         for(int i=2;i<=size;++i)
192             if(!visEdge[i])
193                 dfs(E[i].to,i,++cnt);
194         for(int i=2;i<=size;++i)
195             if(bel[i]!=bel[i^1]&&!vis[make_pair(bel[i],bel[i^1])])
196             {
197                 vis[make_pair(bel[i],bel[i^1])]=1;
198                 G.add(bel[i],bel[i^1]);
199             }
200     }
201 }G,L;
202 //////////////////////////////////////////////////////////////////////////////////////////////
203 int main()
204 {
205     ios::sync_with_stdio(false);
206     return 0;
207 }
View Code

 

 posted on 2019-05-12 19:58  GreenDuck  阅读(190)  评论(0)  编辑  收藏  举报