CF1093E [Intersection of Permutations]

题意

给定整数n两个1-n的排列a,b，有m次操作：
若opt==1，则有 l1 r1 l2 r2，求出a:[l1,r1]与b:[l2,r2]中相同元素的交的大小。
若opt==2,则有 x y，交换b排列中的 第x位与第y位。

n,m≤200,000

思考

只改变b排序中元素位置，考虑每次询问a中l1-r1的元素何时对答案有贡献。

设a中值为i的位置为pi（下标从1开始），b中值为i的位置为qi，则当且仅当[l1,r1]覆盖pi且[l2,r2]覆盖qi时，对答案有贡献。

再换个角度，若只考虑qi，得满足询问的第二个区间包含了qi。

以pi为x轴，qi为y轴建立坐标系，一个询问可以转化为数矩形中有多少个关键点。

那么转换为二维数点。举个例子：

a=[5 1 4 2 3 6]
b=[2 5 3 1 4 6]
询问 a:[2,5]与b[3,6]，在坐标系中的体现就是：

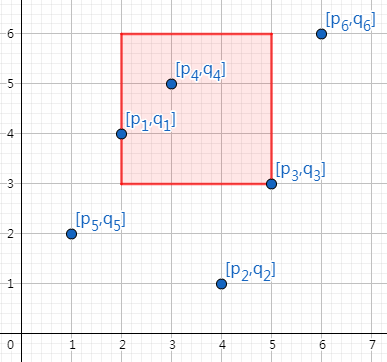
若图还看不懂，看看每个点的下标，再多想一会儿吧。

这样可持久化线段树维护。注意要内存回收（即有很多答案是0的点，这些点完全没有存在的意义，还占空间，只好把他们给 烤了 回收了）。

O(nlogn2)

 

代码

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 const int maxn=2E5+5;
  4 int a[maxn],p1[maxn],p2[maxn],where[maxn],x,y,z,n,m;
  5 int bin[maxn],top;
  6 inline int read()
  7 {
  8     int x=0;
  9     static char ch;
 10     ch=getchar();
 11     while(!isdigit(ch))ch=getchar();
 12     while (isdigit(ch))x=x*10+ch-'0',ch=getchar();
 13     return x;
 14 }
 15 inline void write(int x)
 16 {
 17     if(x==0)putchar('0');
 18     int a[10],size=0;
 19     while(x)
 20     {
 21         a[++size]=x%10;
 22         x/=10;
 23     }
 24     for(int i=size;i>=1;--i)putchar(char(a[i]+'0'));
 25 }
 26 struct BIT
 27 {
 28     int lowbit(int x){return x&-x;}
 29     int root[maxn],cur;
 30     struct tree{int ls,rs,sum;}t[30000000];
 31     void changeT(int l,int r,int pos,int val,int&num,int pre)
 32     {
 33         if(num==0)
 34         {
 35             if(top>0)num=bin[top--];
 36             else num=++cur;
 37         }
 38         t[num]=t[pre];
 39         t[num].sum+=val;
 40         if(l==r)
 41         {
 42             if(t[num].sum==0)
 43             {
 44                 bin[++top]=num;
 45                 num=0;
 46             }
 47             return;
 48         }
 49         int mid=(l+r)>>1;
 50         if(pos<=mid)changeT(l,mid,pos,val,t[num].ls,t[pre].ls);
 51         else changeT(mid+1,r,pos,val,t[num].rs,t[pre].rs);
 52         if(t[num].rs==0&&t[num].ls==0)
 53         {
 54             bin[++top]=num;
 55             num=0;
 56         }
 57     }
 58     void change(int x,int y,int z)
 59     {
 60         for(int i=x;i<=n;i+=lowbit(i))
 61             changeT(1,n,y,z,root[i],root[i]);
 62     }
 63     int askT(int l,int r,int pos,int num)
 64     {
 65         if(pos==0)return 0;
 66         int mid=(l+r)>>1;
 67         if(r==pos)return t[num].sum;
 68         if(pos<=mid)return askT(l,mid,pos,t[num].ls);
 69         else return t[t[num].ls].sum+askT(mid+1,r,pos,t[num].rs);
 70     }
 71     int ask(int l,int r,int pos)
 72     {
 73         int sum=0;
 74         for(int i=r;i;i-=lowbit(i))
 75             sum+=askT(1,n,pos,root[i]);
 76         for(int i=l-1;i;i-=lowbit(i))
 77             sum-=askT(1,n,pos,root[i]);
 78         return sum;
 79     }
 80 }T;
 81 int main()
 82 {
 83 //    freopen("a.in","r",stdin);
 84 //    freopen("a.out","w",stdout);
 85     n=read();m=read();
 86     for(int i=1;i<=n;++i)
 87     {
 88         p1[i]=read();
 89         where[p1[i]]=i;
 90     }
 91     for(int i=1;i<=n;++i)
 92     {
 93         p2[i]=read();
 94         T.change(i,where[p2[i]],1);
 95     }
 96     for(int i=1;i<=m;++i)
 97     {
 98         int opt,L1,R1,L2,R2;
 99         opt=read();
100         if(opt==2)
101         {
102             x=read();y=read();
103             T.change(x,where[p2[x]],-1);
104             T.change(y,where[p2[y]],-1);
105             swap(p2[x],p2[y]);
106             T.change(x,where[p2[x]],1);
107             T.change(y,where[p2[y]],1);
108         }
109         else
110         {
111             L1=read();R1=read();L2=read();R2=read();
112             if(L1>R1)swap(L1,R1);
113             if(L2>R2)swap(L2,R2);
114             write(T.ask(L2,R2,R1)-T.ask(L2,R2,L1-1));
115             putchar('\n');
116         }
117     }
118     return 0;
119 }
View Code

 

 posted on 2019-03-23 21:13  GreenDuck  阅读(170)  评论(0)  编辑  收藏  举报