平面图转对偶图&19_03_21校内训练 [Everfeel]

对于每个平面图，都有唯一一个对偶图与之对应。若G‘是平面图G的对偶图，则满足：

G'中每一条边的两个节点对应着G中有公共边的面，包括最外部无限大的面。

直观地讲，红色标出来的图就是蓝色标出的图的对偶图。

 

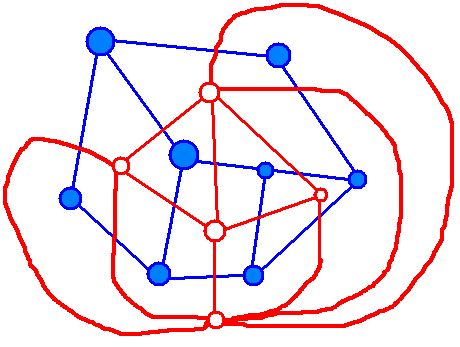
求出一个平面图的对偶图（而且不是特殊的结构），可以贪心地找出所有最小的面。但如何描述最小？我们要固定一条边，按它顺时针或逆时针的方向找到第一条边，直到出现第一个访问过的边，就找到了一个面。

具体地将：从每个边出发，按有方向的角排序，找到角度最大或最小的边，再进行下去。反正自己写写代码就知道了。

 

例题

给出一个平面图，每个点有a和b两种属性，每个面（包括无限大的面）的价值为在这个面上的点的a总和或b总和，若相邻的面所选的属性不同，代价为所有相邻点边的点权和。最大化总价值。N≤4000。

 

思路

考场上从没写过对偶图，结果自己搞出来了.......反而最小割没写出来。

转完对偶图后，从S向每个对偶图上的点连一条比边权为该面的a价值总和的边，再从这个点向T连一条边权为该面的b价值总和的边。对于原图相邻的面，连一条权值为公共边价值和的边（这个要双向）。不难发现其最小割为最小的代价。

如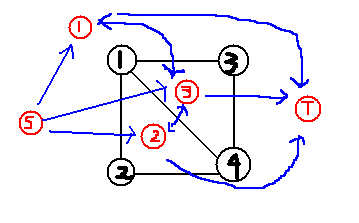：重复的边合并即可。

一个不需要代码的代码：

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 typedef long long int ll;
  4 const double pi=3.1415926535898;
  5 const ll maxn=2E5+5;
  6 const ll inf=INT_MAX;
  7 ll min(ll x,ll y){return x<y?x:y;}
  8 struct pt
  9 {
 10     double x,y;
 11     int pos;
 12     pt(double a=0,double b=0,int p=0){x=a,y=b;pos=p;}
 13     void operator=(pt A){x=A.x,y=A.y,pos=A.pos;}
 14     pt operator+(pt A){return pt(x+A.x,y+A.y,pos);}
 15     pt operator-(pt A){return pt(x-A.x,y-A.y,pos);}
 16     void out(){cout<<x<<" "<<y<<" ";}
 17 }p[maxn];
 18 ll n,m,v[maxn][2],x,y,z,cur,val[maxn][2],ans,dfn[maxn],ti,S,T;
 19 bool vis[maxn*2]; 
 20 map<int,int>next;
 21 map<pair<int,int>,int>cost;
 22 set<pair<int,int> >eS;
 23 pt rotate(pt A,double ra){return pt(A.x*cos(ra)-A.y*sin(ra),A.x*sin(ra)+A.y*cos(ra),A.pos);}
 24 pt wait[maxn];
 25 bool cmp(pt A,pt B)
 26 {
 27     double r1=atan2(A.y,A.x);
 28     double r2=atan2(B.y,B.x);
 29     if(r1<0)r1+=2*pi;
 30     if(r2<0)r2+=2*pi;
 31     return r1<r2; 
 32 }
 33 struct edge{ll to,next,from,w,bel;};
 34 struct graph
 35 {
 36     int head[maxn*2],size;
 37     graph(){size=1;}
 38     edge E[maxn*2];
 39     void add(int u,int v,ll w)
 40     {
 41         E[++size].to=v;
 42         E[size].next=head[u];
 43         E[size].w=w;
 44         E[size].from=u;
 45         head[u]=size;
 46     }
 47     void sortAngle(pt A,pt B,int r,int num)//suppose that A is the centre
 48     {
 49         B=B-A;
 50         double ra=-atan2(B.y,B.x);
 51         B=rotate(B,ra);
 52         for(int i=1;i<=r;++i)wait[i]=rotate(wait[i]-A,ra);
 53         sort(wait+1,wait+r+1,cmp);
 54         next[num]=wait[1].pos;
 55         for(int i=1;i<r;++i)
 56             next[wait[i].pos^1]=wait[i+1].pos;
 57         next[wait[r].pos^1]=num^1;
 58     }
 59     void sortAll()
 60     {
 61         for(int i=2;i<=size;++i)
 62         {
 63             if(next[i]==0)
 64             {
 65                 int L=0;
 66                 for(int j=head[E[i].to];j;j=E[j].next)
 67                 {
 68                     if(E[j].to==E[i].from)continue;
 69                     wait[++L]=p[E[j].to];
 70                     wait[L].pos=j;
 71                 }
 72                 sortAngle(p[E[i].to],p[E[i].from],L,i);
 73             }
 74         }
 75     }
 76     void dfs(int i,int pos)
 77     {
 78         ans+=v[E[i].to][0];
 79         ans+=v[E[i].to][1];
 80         vis[i]=1;
 81         E[i].bel=pos;
 82         val[pos][0]+=v[E[i].to][0];
 83         val[pos][1]+=v[E[i].to][1];
 84         i=next[i];
 85         if(vis[i])return;
 86         dfs(i,pos);
 87     }
 88     void getVal()
 89     {
 90         sortAll();
 91         for(int i=2;i<=size;++i)
 92             if(!vis[i])
 93             { 
 94                 ++cur;
 95                 dfs(i,cur);
 96             }
 97     }
 98     bool bfs()
 99     {
100         for(int i=0;i<=T;++i)dfn[i]=-1;
101         dfn[S]=0;
102         queue<int>Q;
103         Q.push(S);
104         while(Q.size())
105         {
106             int u=Q.front();
107             Q.pop();
108             for(int i=head[u];i;i=E[i].next)
109             {
110                 int v=E[i].to;
111                 if(dfn[v]!=-1||E[i].w==0)continue;
112                 dfn[v]=dfn[u]+1;
113                 Q.push(v);
114             }
115         }
116         return dfn[T]!=-1;
117     }
118     ll dinic(int u,ll up)
119     {
120         if(u==T)return up;
121         ll sum=0;
122         for(int i=head[u];i;i=E[i].next)
123         {
124             int v=E[i].to;
125             if(dfn[v]!=dfn[u]+1||E[i].w==0)continue;
126             ll g=dinic(v,min(E[i].w,up-sum));
127             E[i].w-=g;
128             E[i^1].w+=g;
129             sum+=g;
130             if(g==0)dfn[v]=-1;
131             if(sum==up)break;
132         }
133         return sum;
134     }
135 }G,flow;
136 int main()
137 {
138     freopen("everfeel.in","r",stdin);
139     freopen("everfeel.out","w",stdout);
140     ios::sync_with_stdio(false);
141     cin>>n>>n>>m;
142     for(int i=1;i<=n;++i)
143         cin>>p[i].x>>p[i].y>>v[i][0]>>v[i][1];
144     for(int i=1;i<=m;++i)
145     {
146         cin>>x>>y>>z;
147         G.add(x,y,z);
148         G.add(y,x,z);
149     }
150     G.getVal();
151     S=0;
152     T=cur+1;
153     for(int i=2;i<=G.size;i+=2)
154     {
155         pair<int,int>P=make_pair(G.E[i].bel,G.E[i^1].bel);
156         cost[P]+=G.E[i].w;
157         eS.insert(P);
158     }
159     for(set<pair<int,int> >::iterator pos=eS.begin();pos!=eS.end();++pos)
160     {
161         flow.add(pos->first,pos->second,cost[*pos]);
162         flow.add(pos->second,pos->first,cost[*pos]);
163     }
164     for(int i=1;i<=cur;++i)
165     {
166         flow.add(S,i,val[i][0]);
167         flow.add(i,S,0);
168         flow.add(i,T,val[i][1]);
169         flow.add(T,i,0);
170     }
171     ll sum=0;
172     while(flow.bfs())sum+=flow.dinic(S,inf);
173     cout<<ans-sum<<endl; 
174     return 0;
175 }
View Code
要数据请联系。
 posted on 2019-03-21 18:26  GreenDuck  阅读(492)  评论(0)  编辑  收藏  举报