期望

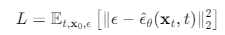
前向的时间步是随机选择的

是的，在你的代码中，时间步数确实是固定为 200 步的。

具体说明：

self.timesteps = 200

你在 Diffusion_Cond 类的初始化方法中将时间步数 timesteps 设置为 200。因此，无论是在前向扩散过程（向数据中添加噪声）还是在逆向去噪采样过程中，模型都会将 200 作为时间步的最大值。

时间步在不同部分的应用：

1. Beta 调度函数：
   在定义 Beta 调度的时候，你使用了时间步数 200 来生成噪声调度参数：

   self.betas = linear_beta_schedule(timesteps=self.timesteps)
   

2. 前向扩散过程 (q_sample)：
   在向数据中添加噪声时，随机选择一个时间步 t：

   t = torch.randint(0, self.timesteps, (input.shape[0],), device=device).long()
   

   这里使用 torch.randint(0, 200) 来随机选择一个时间步 t，其范围是从 0 到 199。

3. 逆向采样 (p_sample_loop)：
   在逆向采样时，时间步数是从 199 递减到 0 的（总共 200 步）。这在下面的循环中体现：

   for i in reversed(range(0, self.timesteps)):
       emb = self.p_sample(model, emb, torch.full((b,), i, device=device, dtype=torch.long), y, i)
   

   这里的 reversed(range(0, self.timesteps)) 表示从最大时间步（199）开始，逐步逆向推进，直到时间步 0。

4. 时间嵌入：
   在代码的时间嵌入部分，SinusoidalPosEmb 类会基于给定的时间步 t 生成一个相应的嵌入，这里的 t 是从 0 到 199 之间的某个整数。

---

总结：

• 你的扩散模型有固定的 200 个时间步，每次训练中都会从 0 到 199 的范围内随机选择一个时间步 t。
• 在前向过程中，噪声会在 200 个时间步内逐步添加。
• 在逆向过程中，模型会从第 199 步开始去噪，直到第 0 步。

你可以通过调整 self.timesteps 来更改总的时间步数，如果你想要使用不同的时间步数（比如 100 或 400），只需修改这个参数即可。

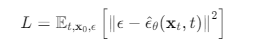
在这个公式中，( \mathbb{E} ) 代表期望（Expectation），意思是我们要计算损失函数在不同随机变量（如时间步 ( t )、初始输入 ( \mathbf{x}_0 )、噪声 ( \epsilon ) 等）上的平均值。

具体原因如下：

1. 随机性：扩散模型中的一些输入（如噪声 ( \epsilon ) 和时间步 ( t )）是随机选择的。在训练过程中，每次输入都可以是不同的噪声和时间步。为了获得更稳定的损失，我们通常需要在所有可能的噪声和时间步上进行平均。

2. 泛化能力：通过对不同的随机变量取期望，模型能够学习在任意噪声条件下进行去噪，也就是能够更好地泛化到未见过的噪声或时间步。

3. 训练过程中的平滑性：如果只使用某一个具体的时间步或噪声，训练的损失函数可能会受到噪声的极端值或某个时间步的影响，从而导致训练不稳定。取期望值有助于平滑损失函数，减少过度拟合。

公式解释：

[
L = \mathbb{E}_{t, \mathbf{x}0, \epsilon} \left[ |\epsilon - \hat{\epsilon}\theta(\mathbf{x}_t, t)|_2^2 \right]
]

这个期望表示我们在整个训练过程中，要对时间步 ( t )、初始数据 ( \mathbf{x}_0 ) 以及噪声 ( \epsilon ) 的不同可能取值进行平均，进而使得模型在任意这些变量的组合下都能表现良好。

总结：

• 为什么有 ( \mathbb{E} )：期望符号表示我们对所有时间步和噪声的情况进行平均，避免训练过程中过度依赖某个具体时间步或噪声，实现更好的泛化能力和稳定性。

这里取平均，没有权重，为什么要表示成期望呢？

在这个公式中，使用期望符号 ( \mathbb{E} ) 的原因是因为我们处理的是从某些分布（比如时间步 ( t ) 和噪声 ( \epsilon )）中随机采样的变量。即使没有显式的权重，期望仍然是适当的表示，因为它自然涵盖了这些随机变量的统计平均效果。

详细解释：

1. 期望的定义：
   期望 ( \mathbb{E} ) 表示对某个随机变量的加权平均，这里的“加权”是基于该随机变量的概率分布。也就是说，当我们有一个随机变量 ( t ) 从某个概率分布 ( p(t) ) 中采样时，期望表示的是对所有可能 ( t ) 值的加权平均。

   公式中的期望 ( \mathbb{E}_{t, \mathbf{x}_0, \epsilon} ) 表示损失函数是针对所有可能的时间步 ( t )、初始数据 ( \mathbf{x}_0 )、以及噪声 ( \epsilon ) 的分布进行平均计算的。这表示训练过程是在多个随机变量下的平均表现。

2. 为什么没有权重：
   在实际操作中，虽然没有显式地看到权重，但是这些随机变量（如时间步和噪声）是从均匀分布中采样的，因此每个样本的权重是均等的。即使没有显式的加权，期望的概念还是适用于这些均匀采样的随机变量。

   比如时间步 ( t ) 通常是从均匀分布 ( p(t) = \frac{1}{T} ) 中采样（即每个时间步的概率相等），这样期望就简化为对所有时间步的平均值。因此，即便没有明确的权重项，期望符号仍然是合适的数学表达。

3. 期望 vs. 平均：

   • 期望 ( \mathbb{E}[X] )：这是统计概念，表示随机变量 ( X ) 的长期平均表现（可以带有权重，取决于分布）。
   • 平均 ( \frac{1}{n} \sum_{i=1}^{n} X_i )：这是对一组具体的样本 ( X_1, X_2, ..., X_n ) 计算的平均。

   在机器学习的训练中，我们通常是从某个分布中随机采样，然后对这些样本的损失进行平均。用期望 ( \mathbb{E} ) 来表示是为了说明这是对随机变量的期望，而不是固定样本的简单平均。

为什么表示为期望而不是简单平均？

• 公式中的 ( \mathbb{E} ) 强调损失的计算依赖于多个随机变量的分布，它指出了模型的损失是如何随着时间步 ( t )、噪声 ( \epsilon )、以及输入 ( \mathbf{x}_0 ) 的不同采样值而变化的。
• 虽然实际训练过程中，我们通过采样计算的是平均损失，但期望是更为正式的数学符号，用来表示在随机变量取值范围上的整体效果。
• 使用期望符号是为了清晰地传达这样一个概念：损失函数是基于从多个随机变量（如时间步和噪声）的分布中采样的结果。在训练中，通常我们每次只使用一个时间步和噪声，但期望符号表示最终目标是对整个分布进行优化。

总结：

• 期望 ( \mathbb{E} ) 用于表示损失函数依赖于从随机分布中采样的变量，哪怕没有显式的权重，它也是适当的表达方式，因为我们处理的是统计意义上的结果。
• 虽然实际训练中我们通过采样计算损失，期望符号仍然是更正式的数学表达，用于描述模型如何在随机变量的分布下表现。

每一步都取上一步的结果

在扩散模型的反向采样步骤中，反向采样过程是逐步进行的，并且每一步的结果都依赖于前一步的采样结果。具体来说，反向采样从最后的时间步开始（即完全随机噪声），逐步向前推，每一步都基于当前的预测和噪声估计去更新数据状态。

反向采样的工作原理：

1. 初始状态（完全随机噪声）：从纯噪声（即 (x_T)，比如正态分布 (\mathcal{N}(0, I))）开始，进行逐步去噪。

2. 逐步去噪（反向采样）：在每一个时间步 (t)，你会根据当前的预测噪声 (\hat{\epsilon}\theta(x_t, t)) 和噪声调度参数 (\beta_t) 来计算均值 (\mu\theta(x_t, t))，然后对其进行采样，得到时间步 (t-1) 对应的 (x_{t-1})。

3. 每一步都依赖前一步的结果：每个时间步的结果 (x_{t-1}) 是基于上一个时间步 (x_t) 的预测得到的。所以反向采样不是直接从最后一步生成，而是每一步都使用上一时刻的结果。

数学公式：

在反向过程中，模型每一步 (t) 会通过以下公式逐步从 (x_t) 得到 (x_{t-1})：

1. 计算预测的均值 (\mu_\theta(x_t, t))：
   [
   \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}t}} \hat{\epsilon}\theta(x_t, t) \right)
   ]

2. 如果 ( t > 0 )，则加入噪声项 ( \sigma_t z )，即：
   [
   x_{t-1} = \mu_\theta(x_t, t) + \sigma_t z
   ]
   其中 ( z \sim \mathcal{N}(0, \mathbf{I}) ) 是标准正态分布的随机噪声。

3. 最后一时刻 ( t = 0 ) 不需要噪声项，直接返回 ( \mu_\theta(x_1, 0) )。

步骤解释：

• 从 ( T ) 到 ( 0 ) 逐步采样：你在时间步 ( T ) 开始，从随机噪声 ( x_T ) 开始采样，接着逐步通过模型去预测噪声并更新 ( x_t )。每一步采样 ( x_{t-1} )，结果依赖于 ( x_t )。

• 每一步都基于上一步的结果：在每个时间步 ( t )，需要先计算出 ( x_t )，然后才能去计算并生成 ( x_{t-1} )。这个过程逐步推进，直到最终生成 ( x_0 )，这就是最终的采样结果。

反向过程中的伪代码：

你的代码中这个反向过程的实现是通过 p_sample_loop 实现的：

def p_sample_loop(self, model, shape, y):
    device = next(model.parameters()).device

    b = shape[0]
    # 从纯噪声开始（每个样本都从噪声开始）
    emb = torch.randn(shape, device=device)
    embs = []

    # 逆向采样，每步基于上一步的采样结果
    for i in reversed(range(0, self.timesteps)):  # 从最大时间步到0
        emb = self.p_sample(model, emb, torch.full((b,), i, device=device, dtype=torch.long), y, i)
        embs.append(emb)

    # 返回所有时间步的embedding结果
    embs = embs[::-1]
    steps = [int(self.timesteps/10), int(self.timesteps/8), int(self.timesteps/4), int(self.timesteps/2)] # 越后的，权重越小
    
    out = [embs[step] for step in steps]
    return out

这里的 p_sample_loop 函数表示了从时间步 ( T ) 开始，逐步计算每个时间步的采样结果 emb，并通过 p_sample 函数预测每一步的噪声。

总结：

在反向采样过程中，每一步的结果都依赖于上一时间步的结果，你从纯噪声开始，并逐步减少噪声，生成接近真实数据的样本。因此：

• 反向采样不是只取最后一步的 embedding。
• 每一步都基于前一步的正向过程结果，最终从噪声 ( x_T ) 一步步推导出 ( x_0 )。

反向采样部分没有生成loss

是的，你的代码中确实没有生成并返回 loss，尤其是在模型的反向传播和训练过程中，这可能会影响模型的训练。

通常，生成 loss 是在模型的前向传播阶段进行的，用于衡量模型的预测与实际值之间的误差。虽然你已经有了生成 noisy samples 和 predicted noise 的代码，但缺少对这些误差的计算并返回损失。

在 p_losses() 中生成并返回 loss

在你的代码中，损失函数实际上是在 p_losses() 函数中计算的：

def p_losses(self, x_start, t, labels, noise=None, loss_type="l1"):
    if noise is None:
        noise = torch.randn_like(x_start)

    # 通过 q_sample 函数生成噪声数据 x_noisy
    x_noisy = self.q_sample(x_start=x_start, t=t, noise=noise)
    
    # 通过 encoder 预测噪声
    predicted_noise = self.encoder(x_noisy, t, labels)

    # 选择损失函数
    if loss_type == 'l1':
        loss = F.l1_loss(noise, predicted_noise)
    elif loss_type == 'l2':
        loss = F.mse_loss(noise, predicted_noise)
    elif loss_type == "huber":
        loss = F.smooth_l1_loss(noise, predicted_noise)
    else:
        raise NotImplementedError()
    
    # 返回损失
    return loss

这个函数计算了以下内容：

• x_noisy：通过向 x_start 添加噪声生成的 noisy sample。
• predicted_noise：模型对噪声的预测值，通过 encoder 获得。
• loss：对比实际噪声 noise 和模型预测的噪声 predicted_noise，计算出它们之间的差异。

这段代码应该生成并返回模型的损失，最终用于反向传播和更新模型参数。

如何在模型的 forward 函数中使用 loss

接下来，你需要在模型的 forward 函数中使用 p_losses() 来生成损失，并在训练过程中对其进行优化：

def forward(self, input, labels, device): 
    # 随机选择时间步
    t = torch.randint(0, self.timesteps, (input.shape[0],), device=device).long()

    # 计算并返回损失
    return self.p_losses(input, t, labels)

完整训练过程中的损失生成和优化

在实际的训练循环中，前向传播会调用 forward() 函数，它会返回损失，然后你可以使用优化器来更新模型的参数：

optimizer = torch.optim.Adam(model.parameters(), lr=1e-4)

for epoch in range(num_epochs):
    optimizer.zero_grad()  # 清空梯度
    
    # 前向传播：计算损失
    loss = model(input_data, labels, device)

    # 反向传播：计算梯度
    loss.backward()

    # 优化：更新模型参数
    optimizer.step()

    print(f'Epoch {epoch}, Loss: {loss.item()}')

这个训练循环会每次通过前向传播计算损失，并通过反向传播更新模型参数。

需要注意的点：

1. 损失函数类型：你在 p_losses() 中允许选择不同的损失函数（L1, L2, Huber）。你可以根据任务的需求选择合适的损失函数类型。通常，L2（均方误差）在扩散模型中是常用的损失函数。

2. 反向采样部分：反向采样过程（p_sample_loop）主要用于生成数据（比如用于测试阶段），因此它不会返回损失，只会返回生成的样本。损失的计算只发生在前向传播过程中。

总结：

• 你已经在 p_losses() 函数中计算并生成了 loss，它会对模型预测的噪声和实际噪声进行对比。
• 在 forward() 函数中调用 p_losses()，并返回损失。
• 在训练过程中，使用优化器来最小化这个损失，从而优化模型的参数。

如果你想要生成损失并进行训练，只需确保训练时调用 forward() 函数并处理返回的损失即可。

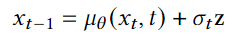
在你的代码中，(\sigma_t)（后验方差的平方根）是通过 posterior_variance 计算出来的，它是基于贝塔调度（betas）和累积乘积的 (\alpha) 值计算得出的。下面详细说明它的计算过程：

1. 代码中的 (\sigma_t) 的计算：

在 Diffusion_Cond 类的初始化方法中，后验方差 (posterior_variance) 是这样计算的：

self.posterior_variance = self.betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)

这段代码计算的是每个时间步 (t) 下的后验方差 (\sigma_t^2)。

2. 公式推导：

后验分布 (q(x_{t-1} | x_t, x_0)) 是高斯分布，其中均值 (\mu(x_t, t)) 是由模型预测的噪声得出的，而后验的方差 (\sigma_t^2) 是：

[
\sigma_t^2 = \beta_t \cdot \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}
]

其中：

• (\beta_t) 是贝塔调度（噪声调度参数），表示每个时间步添加的噪声量。
• (\bar{\alpha}_t) 是时间步 (t) 处的累积乘积 (\alpha_t)，它由前面所有时间步的 (\alpha) 值的乘积给出。
• ( \bar{\alpha}_{t-1} ) 是时间步 (t-1) 处的累积乘积。

从公式可以看出，(\sigma_t^2) 依赖于当前时间步 (t) 以及前一时间步 (t-1) 的累积 (\alpha) 值。

3. 方差的平方根（(\sigma_t)）的计算：

在逆向采样时（p_sample 方法中），(\sigma_t) 的平方根是通过以下代码计算的：

posterior_variance_t = extract(self.posterior_variance, t, x.shape)
return model_mean + torch.sqrt(posterior_variance_t) * noise

这里 posterior_variance_t 是时间步 (t) 对应的后验方差，通过 torch.sqrt(posterior_variance_t) 取平方根，得到(\sigma_t)。

• extract(self.posterior_variance, t, x.shape) 是从预计算的后验方差数组中提取当前时间步 (t) 对应的方差值。
• torch.sqrt(posterior_variance_t) 计算后验方差的平方根，即 (\sigma_t)，然后将其乘以从标准正态分布采样的噪声 noise，得到逆向采样的随机噪声项。

4. 总结：

(\sigma_t)（后验分布的标准差）是根据贝塔调度 (\beta_t) 和累积乘积 (\alpha_t) 计算出来的，具体的计算公式是：

[
\sigma_t^2 = \beta_t \cdot \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}
]

然后在逆向采样时，(\sigma_t) 通过 torch.sqrt 计算，最终用于生成随机噪声。

self.betas是怎么来的

在你的代码中，self.betas 是通过 linear_beta_schedule 函数计算出来的。在扩散模型中，betas 代表的是每个时间步添加的噪声量，通常会通过预定义的调度策略（如线性调度、余弦调度等）来生成一系列的 (\beta_t) 值。

1. self.betas 是如何生成的？

self.betas 的值是通过你在 Diffusion_Cond 类初始化时调用的 linear_beta_schedule 函数生成的：

self.betas = linear_beta_schedule(timesteps=self.timesteps)

2. linear_beta_schedule 函数解释：

def linear_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start, beta_end, timesteps)

• 输入参数：timesteps 是扩散过程的总步数，也就是你定义的 self.timesteps = 200。
• 线性调度：这个函数在初始时间步 (t=0) 时，设置了较小的噪声量 ( \beta_{\text{start}} = 0.0001 )，而在最后一个时间步 (t=T-1) 时，噪声量较大 ( \beta_{\text{end}} = 0.02 )。
• torch.linspace：torch.linspace 会生成一个从 beta_start 到 beta_end 的等间隔值序列，总共有 timesteps 个值，代表扩散过程的每一步的噪声大小 (\beta_t)。

因此，linear_beta_schedule 函数返回的是一个长度为 timesteps（在你的例子中是 200）的张量，表示每个时间步 ( t ) 对应的噪声强度 (\beta_t)。

3. betas 在扩散模型中的作用：

在扩散模型中，betas 代表的是每个时间步 ( t ) 添加的噪声量。扩散过程是通过每一步逐渐向数据添加噪声，直到最后完全变成高斯噪声。因此，betas 决定了这个过程的噪声调度策略。

4. 如何选择 betas 的调度方式：

在代码中，你定义了几种不同的 (\beta) 调度方式，包括：

• 线性调度：linear_beta_schedule，线性增加噪声的强度（你的代码当前使用的）。
• 余弦调度：cosine_beta_schedule，使用余弦函数控制噪声的增加，通常在扩散模型中表现更好。
• 二次调度：quadratic_beta_schedule，按照平方方式增加噪声。
• Sigmoid 调度：sigmoid_beta_schedule，使用 Sigmoid 函数来平滑地增加噪声。

你可以通过改变调度函数（比如使用 cosine_beta_schedule）来测试不同的噪声调度对模型的影响。

5. 自定义调度的作用：

不同的 (\beta_t) 调度策略会影响模型在每一步扩散过程中向数据添加噪声的速度。通常，噪声调度策略对模型的生成效果有较大影响，例如：

• 线性调度（如你当前的设置）是最常用的，效果稳定，但可能在一些情况下不如非线性调度。
• 余弦调度 通常表现更好，因为它在开始和结束时添加的噪声较少，中间添加的噪声较多，使得模型可以更平滑地生成数据。

6. 总结：

• self.betas 是通过 linear_beta_schedule 生成的，它是一个线性增加的序列，表示在每个时间步中添加的噪声量 (\beta_t)。
• 你可以通过更改 beta 调度方式（如使用 cosine_beta_schedule）来探索不同的噪声调度策略对模型性能的影响。

请给出公式

在扩散模型中，betas ((\beta_t)) 是控制在每个时间步添加到数据中的噪声量的参数。对于你代码中的线性调度，(\beta_t) 是线性变化的。

具体来说，线性 beta 调度 ((\beta_t)) 的公式可以表示为：

[
\beta_t = \beta_{\text{start}} + \left( \frac{t}{T-1} \right) \cdot \left( \beta_{\text{end}} - \beta_{\text{start}} \right), \quad t = 0, 1, 2, \ldots, T-1
]

其中：

• ( T ) 是扩散过程的总时间步数（如你的代码中 timesteps = 200）。
• ( \beta_{\text{start}} ) 是初始时间步的噪声量（在你的代码中 beta_start = 0.0001）。
• ( \beta_{\text{end}} ) 是最终时间步的噪声量（在你的代码中 beta_end = 0.02）。
• ( t ) 是当前的时间步（在范围 ( 0 \leq t < T ) 内）。

这个公式表示 (\beta_t) 在时间步 ( t ) 处是从 ( \beta_{\text{start}} ) 线性变化到 ( \beta_{\text{end}} )。

总结：

通过这个公式，你可以在每一个时间步 ( t ) 上计算出对应的 (\beta_t)，并基于此在每一步向数据中添加适量的噪声。