hdu 5955 Guessing the Dice Roll 【AC自动机+高斯消元】

hdu 5955 Guessing the Dice Roll 【AC自动机+高斯消元】

题意：给出 n≤10 个长为 L≤10 的串，每次丢一个骰子，先出现的串赢，问获胜概率。

题解：裸的AC自动机，求匹配到终止结点的概率，用 高斯消元？一开始不知道怎么建方程组，直接举个例子吧：

Input:

1

2 2

1 1

2 1

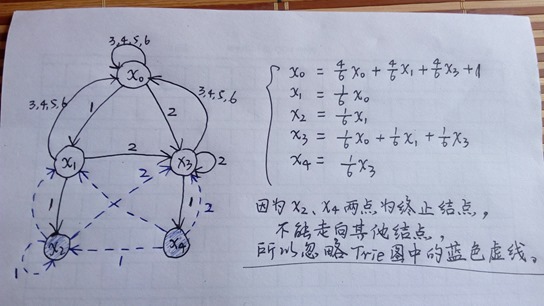
图解：

x0原本概率就是1，然后还要加上其他结点走向它的概率，，这样最后算下来是大于1的，现在还是觉得怪怪的。。。

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;
const int N = 105;
const int M = 6;
int equ, var;
double a[N][N];
double x[N];
void Gauss() {
    int i, j, k;
    int max_r;
    int col;
    for(col = 0, k = 0; k < equ && col < var; ++k, ++col) {
        max_r = k;
        for(i = k+1; i < equ; ++i)
            if(fabs(a[i][col]) > fabs(a[max_r][col]))
                max_r = i;
        if(max_r != k) {
            for(j = k; j < var; ++j)
                swap(a[k][j], a[max_r][j]);
               swap(x[k], x[max_r]);
        }
        x[k] /= a[k][col];
        for(j = col+1; j < var; ++j)
            a[k][j] /= a[k][col];
        a[k][col] = 1;
        for(i = 0; i < equ; ++i) {
            if(i != k) {
                x[i] -= x[k] * a[i][col];
                for(j = col+1; j < var; ++j)
                    a[i][j] -= a[k][j] * a[i][col];
                a[i][col] = 0;
            }
        }
    }
}
int mk[N];
struct Trie {
    int next[N][M], fail[N], tag[N];
    int root, L;
    int newnode() {
        for(int i = 0;i < M;i++)
            next[L][i] = -1;
        tag[L++] = 0;
        return L-1;
    }
    void init() { L = 0; root = newnode(); }
    void Insert(int buf[], int len, int id) {
        int u = root;
        for(int i = 0; i < len; i++) {
            if(next[u][buf[i]] == -1)
                next[u][buf[i]] = newnode();
            u = next[u][buf[i]];
        }
        tag[u] = 1;
        mk[id] = u;
    }
    void build() {
        queue<int> Q;
        fail[root] = root;
        for(int i = 0; i < M; i++) {
            if(next[root][i] == -1)
                next[root][i] = root;
            else {
                fail[next[root][i]] = root;
                Q.push(next[root][i]);
            }
        }
        while( !Q.empty() ) {
            int u = Q.front();
            Q.pop();
            for(int i = 0; i < M; i++) {
                int &v = next[u][i];
                if(v == -1)
                    v = next[fail[u]][i];
                else {
                    Q.push(v);
                    fail[v] = next[fail[u]][i];
                }
            }
        }
    }
    void query(int n) {
        int i , j;
        CLR(a, 0); CLR(x, 0);
        equ = var = L;
        for(i = 0; i < L; ++i) a[i][i] = -1.0;
        x[0] = -1.0;
        for(i = 0; i < L; ++i) {
            for(j = 0; j < M; ++j) {
                if(next[i][j] != -1 && tag[i]==0)
                    a[next[i][j]][i] += 1.0/6;
            }
        }
        Gauss();
        for(i = 0; i < n-1; ++i)
            printf("%.6f ", x[mk[i]]);
        printf("%.6f\n", x[mk[n-1]]);
    }
};
Trie ac;
int main() {
    int T, n, m;
    int A[15];
    scanf("%d",&T);
    while( T-- ) {
        scanf("%d%d", &n, &m);
        ac.init();
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; ++j) {
                scanf("%d", &A[j]);
                A[j]--;    //0~5
            }
            ac.Insert(A, m, i);
        }
        ac.build();
        ac.query(n);
    }
    return 0;
}