MVP矩阵变换详解

目录

• 概念
• 模型变换（Modeling Transformation）
  • Scale
  • Rotate
  • Translate
• 视图变换（View Transformation）
  • Translate
  • Rotate
• 投影变换（Projection Transformation）
  • 正交投影
  • 透视投影
• 视口变换
• 最终公式

概念

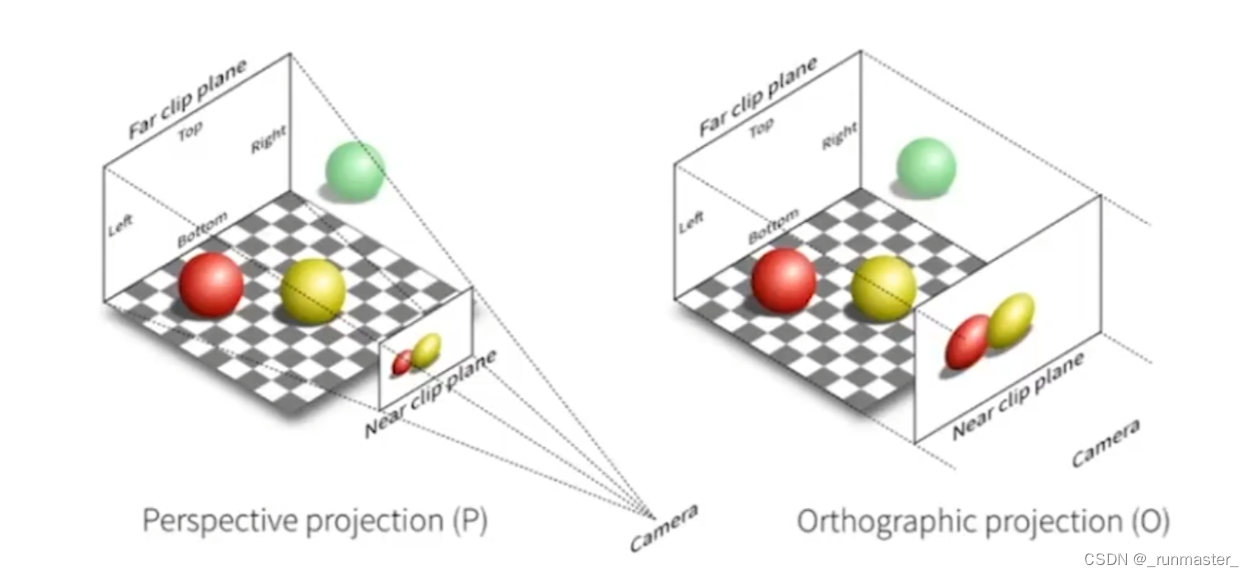
MVP变换是图形学中将三维空间里的物体呈现在二维屏幕上的一种方法。

• M(Model)模型变换
• V(View)视图变换
• P(Projection)投影变换

模型变换将物体从局部空间变换到世界空间中，通过视图变换从世界空间转换到相对于摄像机的观察空间，再通过投影变换将物体从观察空间转换到裁剪空间。其实在投影变换后面应该还有一步E(Viewport)视口变换，该变换进行齐次除法，得到归一化坐标，最后进行屏幕映射，将归一化坐标转化为屏幕上的像素坐标。

模型变换（Modeling Transformation）

模型变换是将物体从局部空间变换到世界空间的一个矩阵，这个矩阵是随着物体的运动而改变的。

• 局部空间

局部空间是每个物体自身的坐标系，它可以方便地描述物体的形状和结构，而不受其他物体或场景的影响。局部空间的原点一般是物体的中心点或重心点，这样可以简化物体的旋转和缩放操作。
举个例子，在UE里，每个你选中的小物体都有一个局部坐标系，这是以物体自身为参照，和世界坐标系分离开来的独立的坐标系

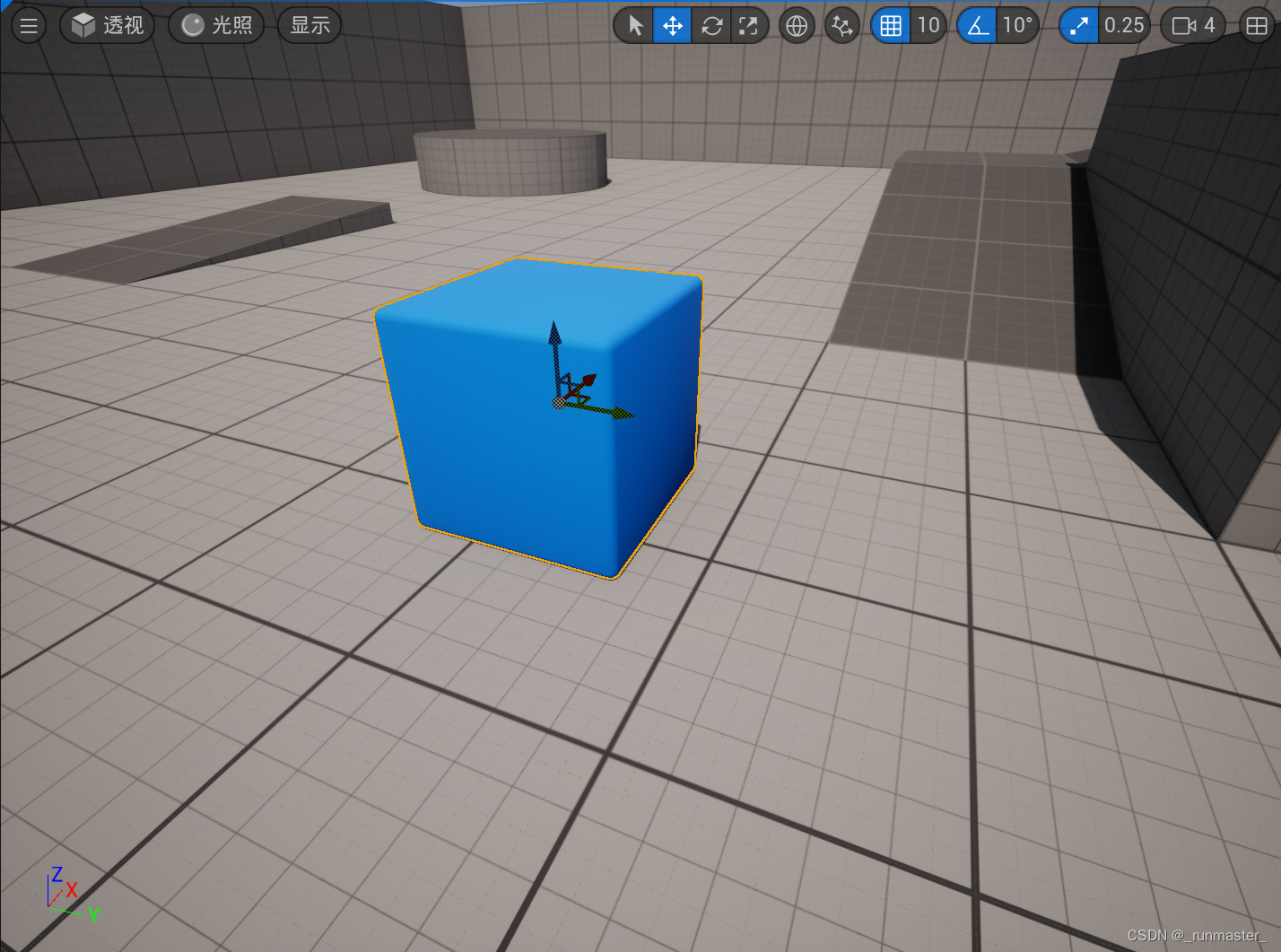
• 世界空间

世界空间是整个场景的坐标系，它可以统一地表示所有物体在场景中的位置和方向，以及相互之间的关系。世界空间的原点和轴一般是固定不变的，这样可以方便地进行视图变换和投影变换。
举个例子，能看到的移动一般都发生在世界空间，我们点击移动的物体对比一下就可以发现，一个物体在世界坐标下发生了移动，但是若以他本体为参考物他是不动的

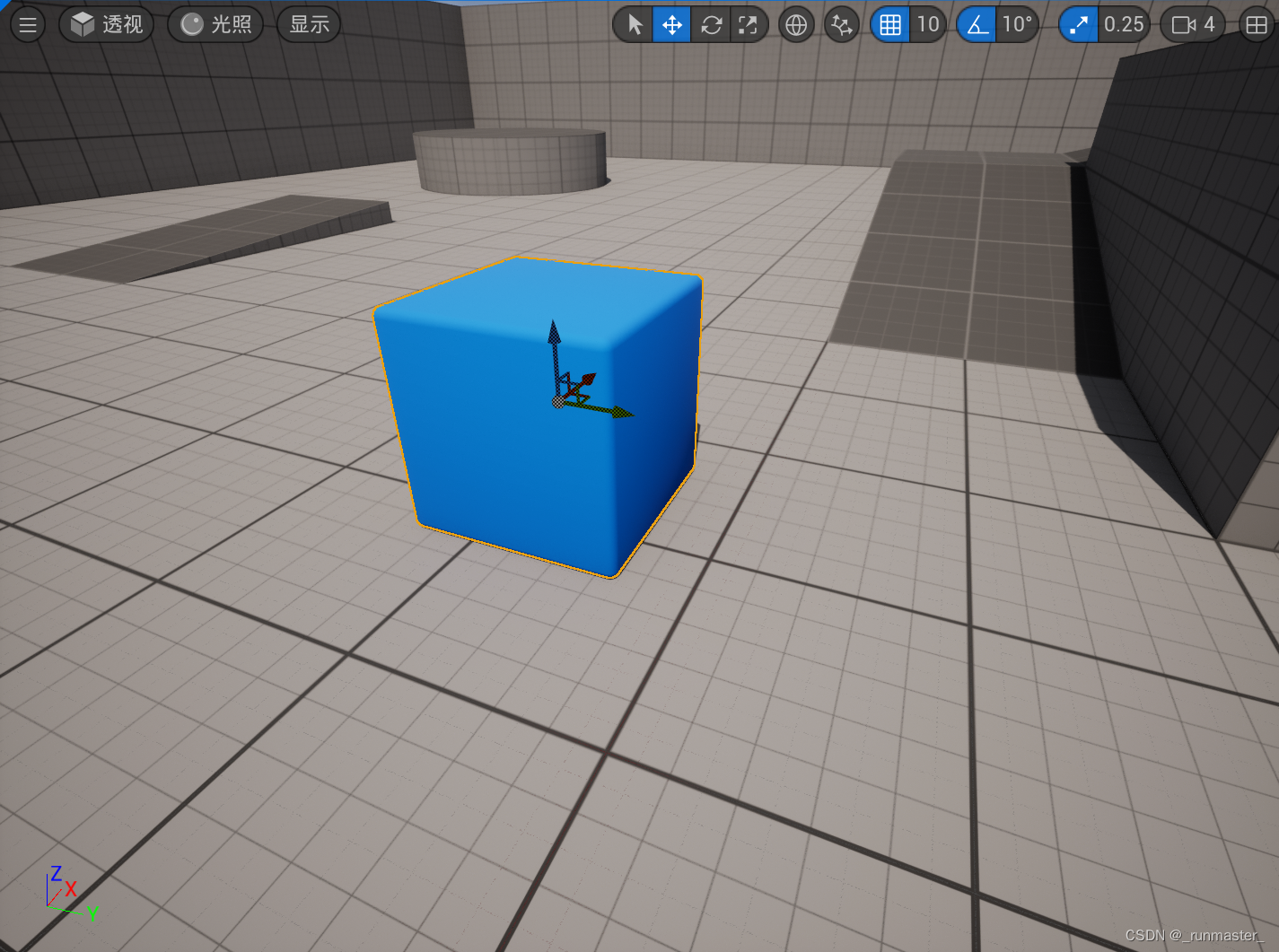
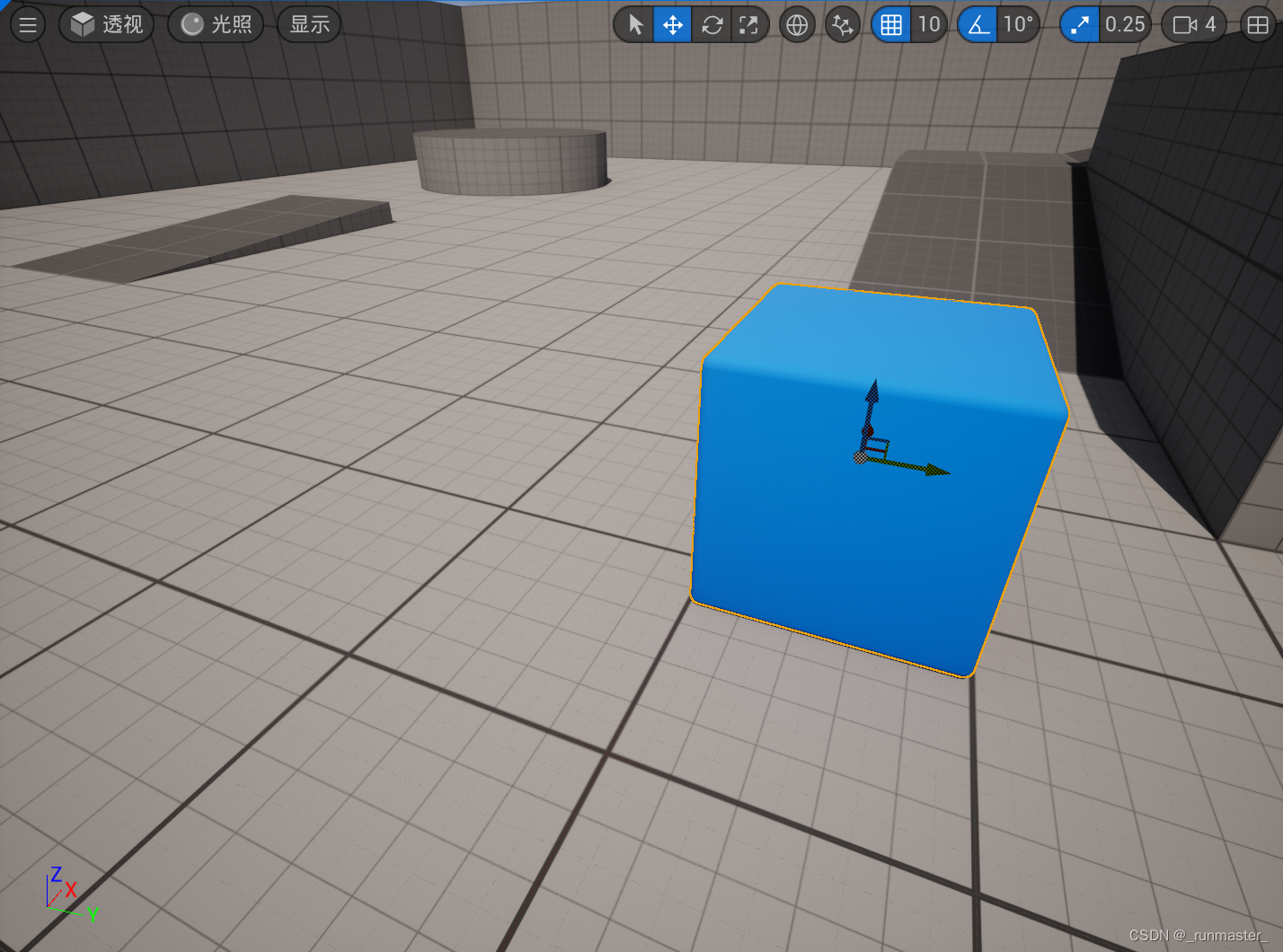
• 为什么需要区分局部空间和世界空间？

通过区分局部空间和世界空间，我们可以实现物体的复用和实例化，即用同一个局部空间定义的物体，在不同的世界空间位置、方向和比例绘制多次，从而节省内存和提高效率。

通过区分局部空间和世界空间，我们也可以实现物体的层级关系和动画效果，即用一个物体作为父节点，定义其子节点的局部空间相对于父节点的世界空间的变换，从而使子节点随父节点一起移动和旋转。

• 如何进行局部空间到世界空间的变换？

我们一般通过将局部空间的坐标点乘一个变换矩阵来得到他在世界空间的位置

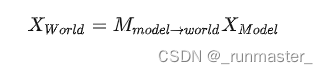
但是在世界空间中，物体可不止有位移，还有旋转和缩放，所以Model矩阵可以拆分成Translate、Rotate和Scale三个矩阵的点乘

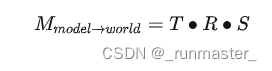
要注意，这里位移和旋转矩阵的顺序不同得到的结果也是不一样的，因为不管是位移还是选择，作用的对象其实是局部坐标系，移动和旋转的原点都是原本局部坐标系下的原点，不同操作顺序得到的结果截然不同。

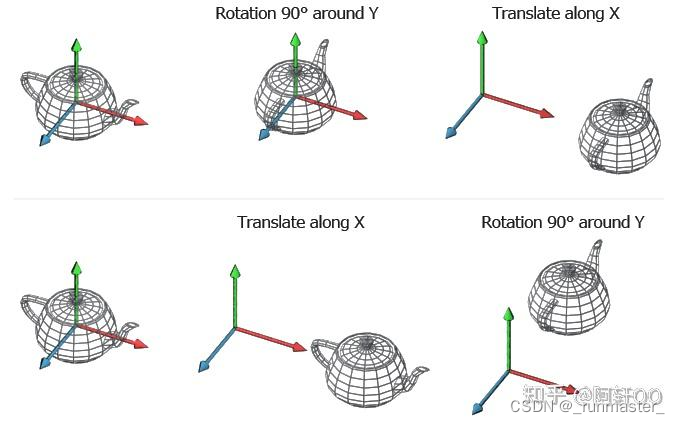
上图中上半部分结果是先旋转再平移，下半部分结果是平移后再旋转，一般情况下，我们Model矩阵执行顺序为Scale、Rotate、Translate。

Scale

Scale矩阵用来对物体进行缩放，我们用齐次矩阵来表示

$Scale=\left[\begin{array}{cccc}Sx& 0& 0& 0\\ 0& Sy& 0& 0\\ 0& 0& Sz& 0\\ 0& 0& 0& 1\end{array}\right]$

注意，点乘的顺序不同结果也是不一样的，这里我们点乘的顺序可以从右到左来记：坐标点乘Scale

$Scale\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}Sx\ast x\\ Sy\ast y\\ Sz\ast z\\ 1\end{array}\right]$

Rotate

Rotate矩阵用来计算旋转，旋转矩阵相对于缩放矩阵而言较为复杂。
这里的旋转我们用欧拉角来表示

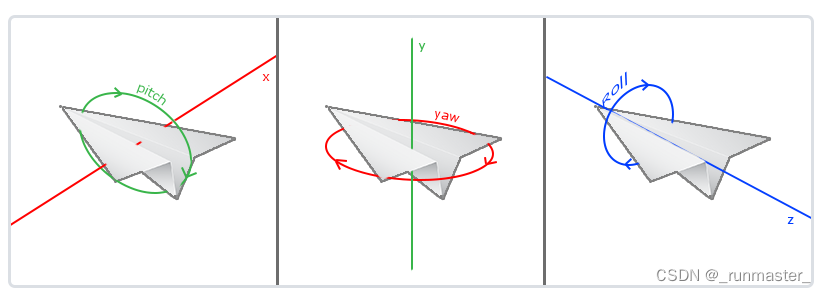
参照上图，我们可以理解为：

• 绕X轴旋转，即绕pitch（俯仰角）旋转
• 绕Y轴旋转，即绕yaw（航向角）旋转
• 绕Z轴旋转，即绕roll（翻滚角）旋转

所以我们可以用三个轴的旋转来综合表示任意旋转
举个例子：
假设P绕X轴旋转θ度得到Pr，我们需要求这个旋转矩阵

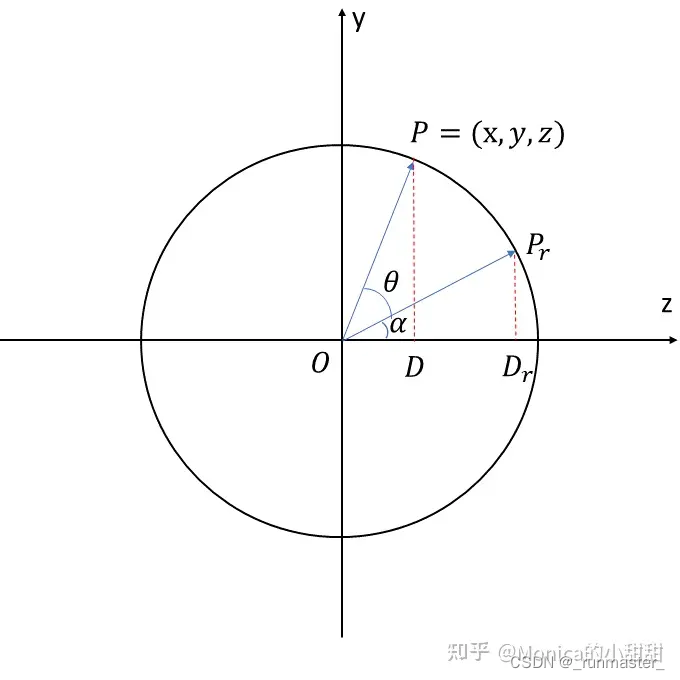
我们的目的是得到一个矩阵，使得

$Pr=M\theta \cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

已知Pr、P的坐标，化简得

$\left[\begin{array}{c}x\\ \sin \alpha \\ \cos \alpha \\ 1\end{array}\right]=M\theta \cdot \left[\begin{array}{c}x\\ \sin (\alpha +\theta )\\ \cos (\alpha +\theta )\\ 1\end{array}\right]$

解上面的矩阵并不是一个容易的事情，我们采用几何上的解法

$y=\sin (\theta +\alpha )=\sin \theta \cos \alpha +\cos \theta \sin \alpha$
$z=\cos (\theta +\alpha )=\cos \theta \cos \alpha -\sin \theta \sin \alpha$

y、z分别乘sinθ和cosθ

$y\sin \theta ={\sin }^2\theta \cos \alpha +\sin \theta \cos \theta \sin \alpha$
$z\cos \theta ={\cos }^2\theta \cos \alpha -\sin \theta \cos \theta \sin \alpha$

相加化简得到最后结果

$\cos \alpha =y\sin \theta +z\cos \theta$
$\sin \alpha =y\cos \theta -z\sin \theta$

根据上面公式，我，们可以推倒得出Mθ的结果

$M\theta x=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$

即

$Pr=M\theta \cdot P=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$

我们以此类推后续分别可以得到绕Y和绕Z轴旋转θ度的矩阵

$M\theta z=\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin \theta & \cos \theta & 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right]$

$M\theta y=\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 0& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$

在得到了旋转矩阵以后，我们还需要注意一个问题，就是对不同轴的旋转顺序会影响最后的旋转结果，详细可以看看这个视频

Translate

Translate变换的目的就是计算物体的位移，而计算位移最简单的思想是加法。由于MVP都是矩阵的形式，加法不是佷适用，所以这里我们用一个齐次矩阵直接替换掉原来的加法，原坐标点乘这个齐次矩阵就可以得到位移结果了

$Translate=\left[\begin{array}{cccc}1& 0& 0& Tx\\ 0& 1& 0& Ty\\ 0& 0& 1& Tz\\ 0& 0& 0& 1\end{array}\right]$

得到结果

$Translate\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}x+Tx\\ y+Ty\\ z+Tz\\ 1\end{array}\right]$

在得到上面结果以后我们便可以得到完整的Model模型变换矩阵

$Model=Translate\cdot Rotate\cdot Scale$

一定要注意点乘顺序，我们需要从右往左来看

视图变换（View Transformation）

模型变换将物体变换到世界坐标下了，接下来是经过视图变换将物体从世界坐标转换到摄像机视角下的视图空间，这样才可以确定哪些物体需要被看到从而渲染出来。视图空间变换分为两步：

1. 确认摄像机位置（Translate）
2. 确实摄像机朝向（Rotate）

这两步操作其实沿用了模型变换的思想，View矩阵可以被拆分成Translate和Rotate两个矩阵的点乘。

Translate

视图变换中我们需要以摄像机为原点来构建坐标系，再将世界空间下的模型坐标转换到视图空间里面。
在视图变换中，我们默认摄像机坐标为原点，我们要计算的是世界空间中各个物体相对于摄像机的位置。我们可以换一种理解方式：假设摄像机位置是(Px,Py,Pz),既然视图变换需要以摄像机为原点，那么我们把摄像机移回世界空间的原点，而物体相对于摄像机位置是不变的，所以也需要进行同样的移动，这个时候我们可以求出该变换矩阵

$Translate=\left[\begin{array}{cccc}1& 0& 0& -Px\\ 0& 1& 0& -Py\\ 0& 0& 1& -Pz\\ 0& 0& 0& 1\end{array}\right]$

因为相对坐标没有发生变化，所以此时所有物体都点乘这个矩阵后得到的位置就可以理解为是以摄像机为原点所看到的物体应处于的位置，也就是各物体在视图空间下的位置。

Rotate

但是其实仅通过Translate矩阵不完全正确，因为摄像机是会旋转的，所以我们需要在他旋转的同时给所有物体也点乘一个旋转矩阵才行。

在这里我们需要注意的是，摄像机的旋转和上面模型变换中的旋转是不同的，因为模型变换是旋转本身，而此时的摄像机旋转是旋转以摄像机为原点的整个坐标系

• 如何旋转坐标系？
  在UE和Blender里面坐标系其实有一些区别
  UE
  
  Blender
  
  由上图可以看出，UE用的是左手坐标系、Blender用的是右手坐标系
  

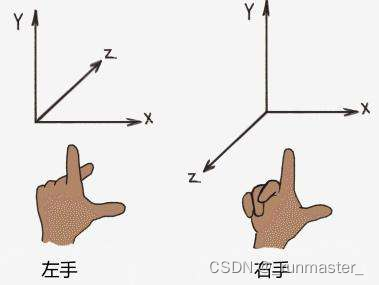
所以假设当我们在建模的时候，以Blender坐标系为准，但是转换到UE，我们需要点乘一个矩阵M来调整坐标系
我们可以理解为，右手坐标系的z轴是跟左手坐标系的z轴是反向的，所以在UE中我们只需要把Blender导出的物体的z轴全部反向即可，也就是乘以下矩阵

$M=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right]$

而我们要算的摄像机的旋转跟上面同理，也就是通过乘某个矩阵来旋转坐标系

举个例子

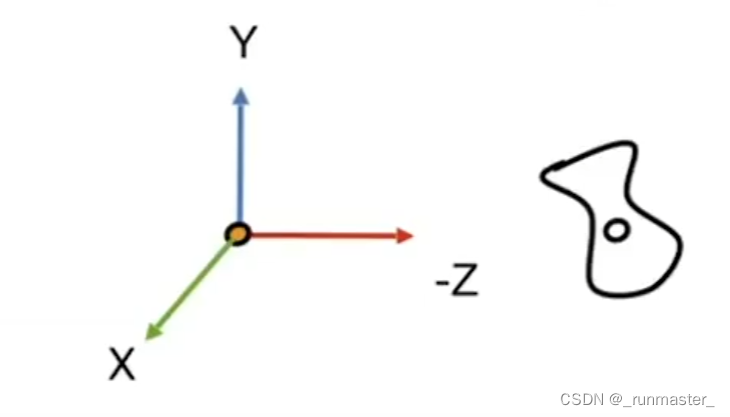
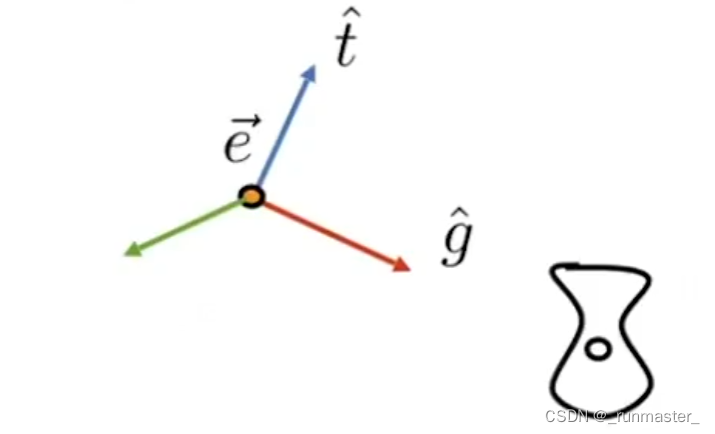
e、t、g是摄像机的坐标系。
我们需要把X、Y、Z坐标系转换到e、t、g坐标系。
直接计算该矩阵略显复杂，我们可以通过逆运算来计算。我们需要求X、Y、Z坐标系转换到e、t、g坐标系所需要的Rotate矩阵，我们可以通过求e、t、g到X、Y、Z变换矩阵的逆矩阵得到，即

$Rotate\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}e\\ t\\ g\\ 1\end{array}\right]$

$Rotat{e}^{-1}\cdot Rotate\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=Rotat{e}^{-1}\cdot \left[\begin{array}{c}e\\ t\\ g\\ 1\end{array}\right]$

我们可以轻松得到

$Rotat{e}^{-1}=\left[\begin{array}{cccc}{x}_{g\times t}& x_t& x_{-g}& 0\\ y_{g\times t}& y_t& y_{-g}& 0\\ z_{g\times t}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$

由于正交矩阵的性质，我们可以得到

$Rotate=\left[\begin{array}{cccc}{x}_{g\times t}& y_{g\times t}& z_{g\times t}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$

接下来我们来将物体从世界空间转换到摄像机空间的Rotate矩阵

1. 我们假设Dir为摄像机视角下的Z轴，也就是摄像机的朝向
2. 假设一个Up向量(0,1,0)
3. 用Up向量和Dir向量叉乘算出X轴$R=cross(Up,Dir)$
4. 用算出的R向量和Dir向量叉乘算出Y轴$U=cross(R,Dir)$

即

$Rotate=\left[\begin{array}{cccc}{R}_x& R_y& R_z& 0\\ U_x& U_y& U_z& 0\\ Di{r}_x& Di{r}_y& Di{r}_z& 0\\ 0& 0& 0& 1\end{array}\right]$

得到最终结果

$View=Rotate\cdot Translate=\left[\begin{array}{cccc}{R}_x& R_y& R_z& 0\\ U_x& U_y& U_z& 0\\ Di{r}_x& Di{r}_y& Di{r}_z& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{cccc}1& 0& 0& -Px\\ 0& 1& 0& -Py\\ 0& 0& 1& -Pz\\ 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{cccc}{R}_x& R_y& R_z& -R\cdot P\\ U_x& U_y& U_z& -U\cdot P\\ Di{r}_x& Di{r}_y& Di{r}_z& -D\cdot P\\ 0& 0& 0& 1\end{array}\right]$

投影变换（Projection Transformation）

经过视图变换以后，物体成功转换到了摄像机视角下了，我们需要一个投影矩阵把摄像机看到的画面投影到我们指定大小的屏幕空间里。

而投影分为两种，正交投影和透视投影，而投影变换和正交变换关系密不可分。
正交投影是直接把物体坐标从视图空间转换到标准化设备空间（NDC），透视投影则需要先进行一轮变换，把透视投影压缩成正交投影，再通过正交投影把坐标变换到NDC空间。

正交投影

在正交投影里面，我们无法通过视觉来判断远近关系，因为其视锥体是长方体，不管远近物体的成像只基于本身的大小。

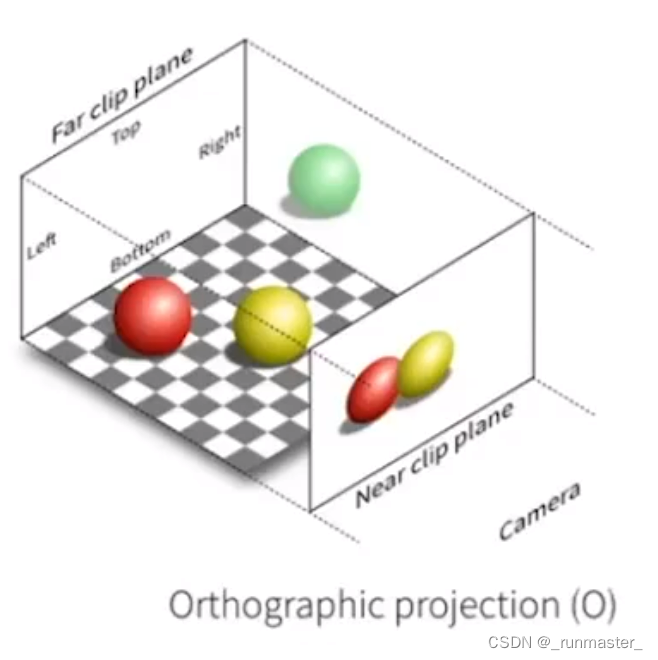
正交投影可以分为两步

1. 选定一个范围的视锥体空间，该视锥体决定了可以看到视野的范围。
2. 把该视锥体空间平移到取值范围为$[-1,1{]}^3$的2*2*2的立方体内

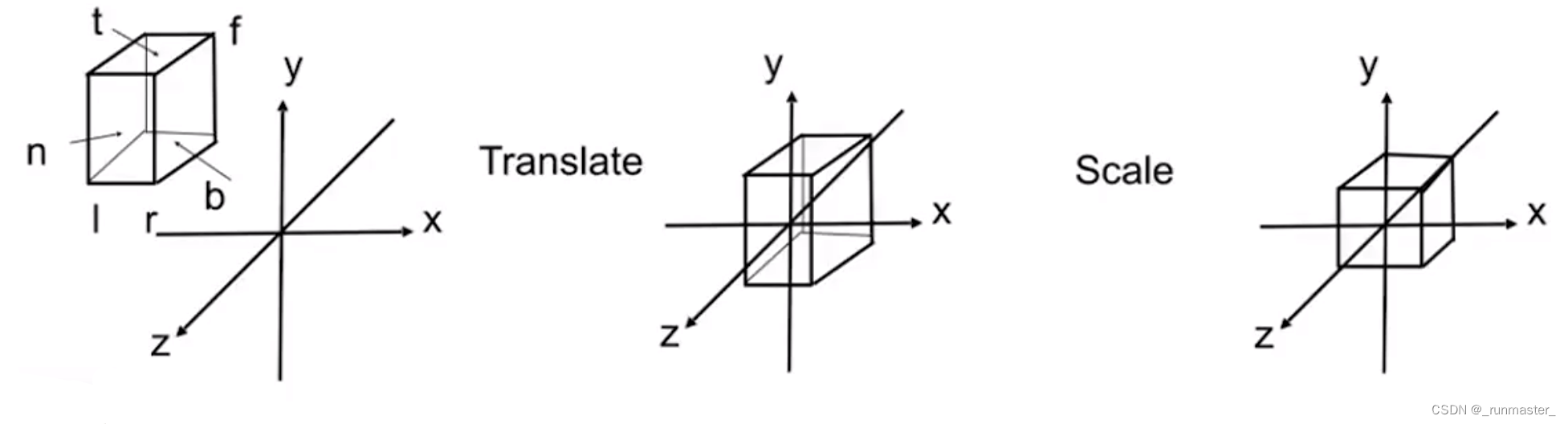
上图中的t、b、l、r、n、f分别是该视锥体对应方向的最大值和最小值，我们通过这些值来计算位移矩阵。
经过位移计算后我们对每条边分别除以他们的长度再乘2便可以得到范围是$[-1,1{]}^3$的2*2*2的立方体了。

$M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& \frac{l+r}{l-r}\\ 0& \frac{2}{t-b}& 0& \frac{b+t}{b-t}\\ 0& 0& \frac{2}{n-f}& \frac{f+n}{f-n}\\ 0& 0& 0& 1\end{array}\right]$

透视投影

透视投影符合我们实际的观察情况，满足“近大远小”的规则。

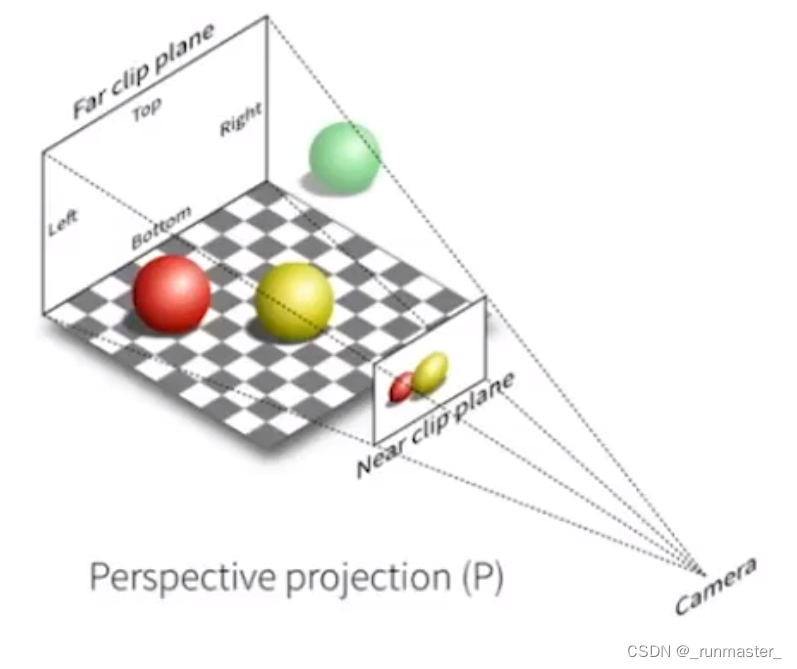
透视投影分为两步

1. 把视锥体的远裁剪平面缩小到和近裁剪平面一样，相当于把锥形视锥体的尾部压扁，变成长方形视锥体
2. 通过正交投影把该视锥体投影到NDC空间

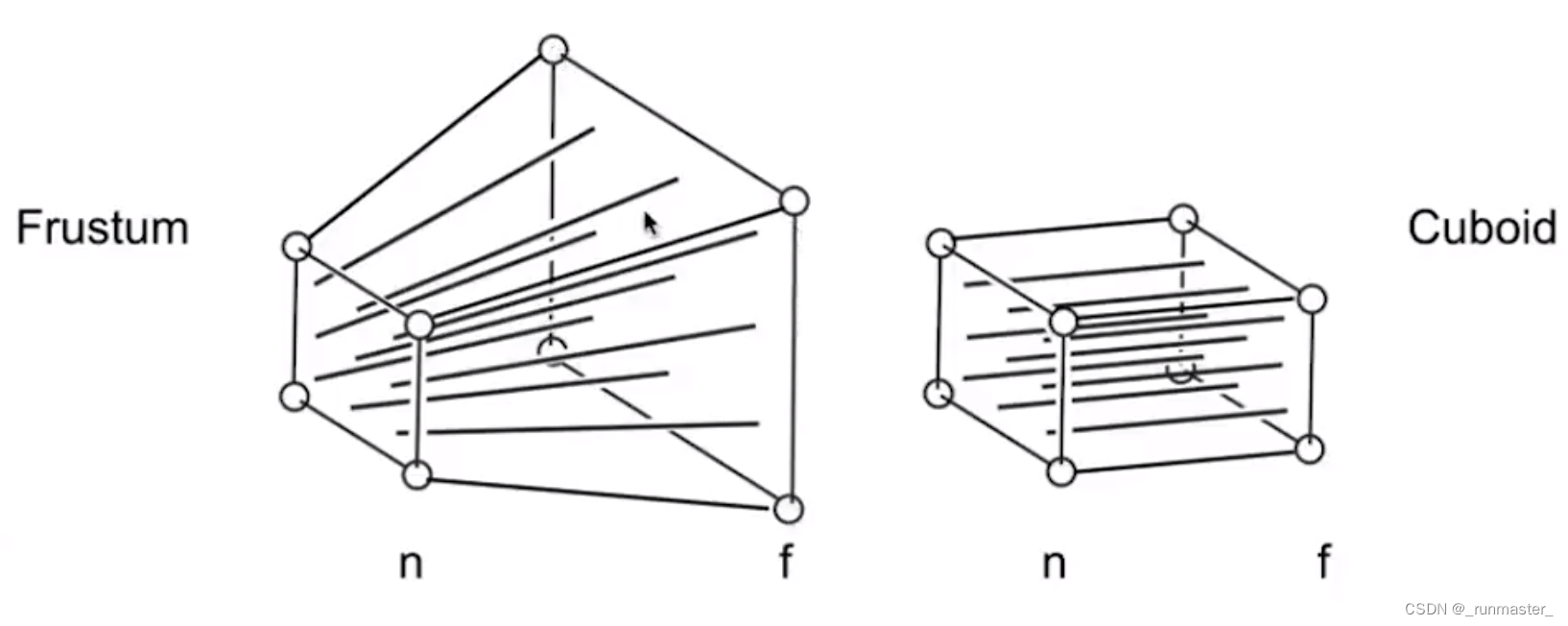
那么我们要如何把锥体内所有顶点压缩到长方体内呢？
我们先来看椎体的横截面

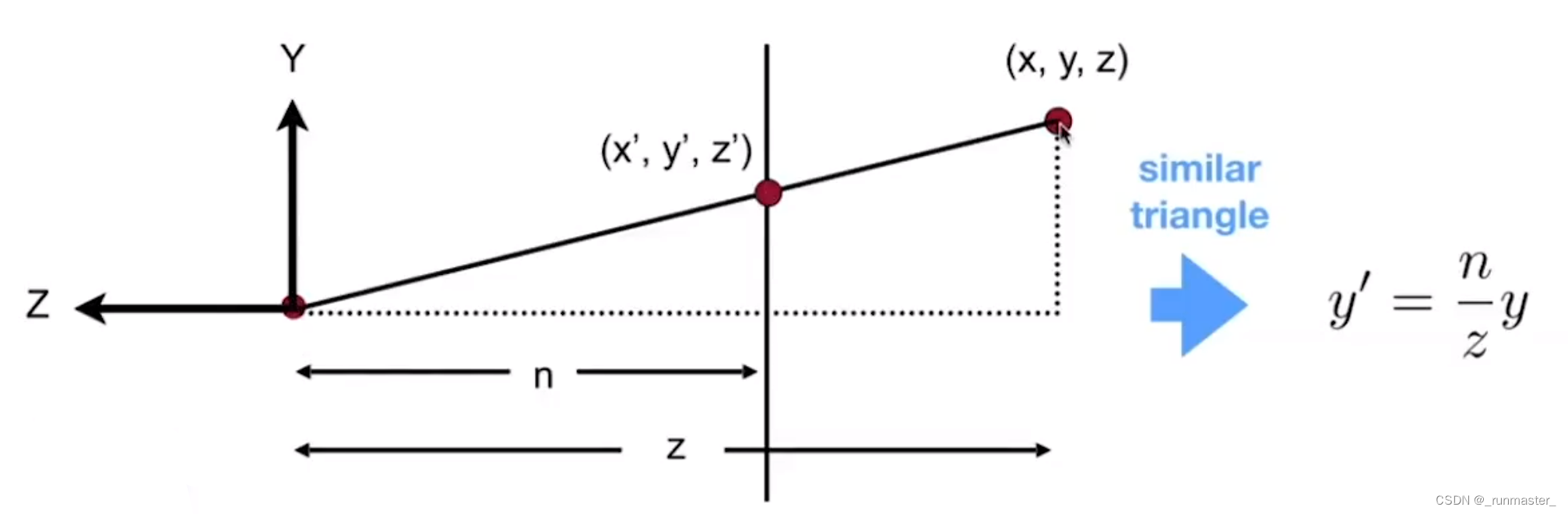
利用三角形的相似关系不难看出

$y^{\prime }=\frac{n}{z}y$

$x^{\prime }=\frac{n}{z}x$

我们可以通过透视空间的z来计算出变换后的$x^{\prime }$和$y^{\prime }$，但是在透视空间变换到正交空间的过程中$z^{\prime }$的变换是非线性的，这样就导致了我们很难通过想象去理解$z^{\prime }$和$z$的关系。

$(x^{\prime },y^{\prime },z^{\prime })=(\frac{n}{z}x,\frac{n}{z}y,?)$

为了计算$z^{\prime }$和$z$的关系，我们把上述在笛卡尔坐标系上的值转化到齐次坐标系上
也就是加上一个维度的$w$来进行透视除法把点转换到正交空间上。
这里需要注意在正交投影里不存在近大远小所以齐次坐标的$w$分量都为1
这里的n=$z_{near}$

$(\frac{n}{z}x,\frac{n}{z}y,?)\to (\frac{n}{z}x,\frac{n}{z}y,?,1)=(nx,ny,?,z)$

我们根据已知的数据可以推断出一个不完全的$M_{persp\to ortho}$矩阵

$M_{persp\to ortho}\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}nx\\ ny\\ ?\\ z\end{array}\right]$

$M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right]$

我们最终的目的就是求解这个矩阵
我们梳理一下已知信息：

1. 在近平面和远平面这两个特殊的面上，$z^{\prime }$分别等与$z_{near}$和$z_{far}$，也就是在这两个平面上$z^{\prime }$=$z$
2. 变换后的远裁剪平面的中心点坐标保持不变
3. 近裁剪平面上的点坐标不发生变化

我们结合远近平面的信息，可以采用特殊值法来解上面的矩阵

• 根据近平面数据求方程1

已知$n=z_{near}$且$z=n$

$M_{persp\to ortho}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right]=\left[\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right]$

$n^2$只与$n$有关，所以我们可以补全一些$M_{persp\to ortho}$的信息

我们把?用A、B代替

$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]\left[\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right]=n^2$

得出方程1

$An+B=n^2$

• 根据远平面数据求方程2

已知$f=z_{far}$且$z=f$,且变换后的远裁剪平面的中心点坐标保持不变
我们以远平面中心点作为特殊值

$M_{persp\to ortho}\left[\begin{array}{c}0\\ 0\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ f^2\\ f\end{array}\right]$

$f^2$只与$f$有关，所以我们可以补全一些$M_{persp\to ortho}$的信息

$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]\left[\begin{array}{c}x\\ y\\ f\\ 1\end{array}\right]=f^2$

得出方程2

$Af+B=f^2$

• 求解$M_{persp\to ortho}$矩阵

结合方程1和方程2

$An+B=n^2$
$Af+B=f^2$

我们得出A、B的值

$A=n+f$
$B=-nf$

补全$M_{persp\to ortho}$

$M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]$

在完成了透视投影到正交投影的变换后我们还需要把投影转换到NDC空间里面

$M_{persp}=M_{ortho}\cdot M_{persp\to ortho}$

$M_{persp}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& \frac{l+r}{l-r}\\ 0& \frac{2}{t-b}& 0& \frac{b+t}{b-t}\\ 0& 0& \frac{2}{n-f}& \frac{f+n}{f-n}\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]=\left[\begin{array}{cccc}\frac{2n}{r-l}& 0& \frac{l+r}{l-r}& 0\\ 0& \frac{2n}{t-b}& \frac{b+t}{b-t}& 0\\ 0& 0& \frac{n+f}{n-f}& \frac{2nf}{f-n}\\ 0& 0& 1& 0\end{array}\right]$

视口变换

在MVP变换之后需要视口变换从NDC空间变换到屏幕空间上，这里的屏幕空间并不是UV空间，而是范围是[0,width]×[0,width]的空间

视口变换为$M_{viewport}$
$M_{viewport}=\left[\begin{array}{cccc}\frac{width}{2}& 0& 0& \frac{width}{2}\\ 0& \frac{height}{2}& 0& \frac{height}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$

最终公式

$\left[\begin{array}{c}{x}_{new}\\ y_{new}\\ z_{new}\\ 1\end{array}\right]=M_{view}\cdot P_{persp}\cdot View\cdot Model=M_{view}\cdot P_{persp}\cdot (Rotate\cdot Translate)\cdot (Translate\cdot Rotate\cdot Scale)\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$
上面只是MVP的结果，但需要注意的是MVP变化后Vertex Shader的输出是在Clip Space[w,-w]上，需要由GPU自己做透视除法到NDC[-1,1]空间，最后屏幕里的坐标需要通过视口变换变到屏幕空间[0,w][0.h]
参考文章
GAMES101计算机图形学学习笔记
图形学论文解析与复现
从左手坐标系到右手坐标系的变换