GAMES202作业4
作业要求
微表面模型的 BRDF(Microfacet BRDF) 存在一个根本问题,就是忽略了微平面间的多次弹射,这就导致了材质的能量损失,并且当材质的粗糙度越高时,能量的损失会越严重。通过引入一个微表面 BRDF 的补偿项,来补偿光线的多次弹射,使得材质的渲染结果可以近似保持能量守恒,这个 BRDF 的补偿模型就是本轮作业需要重点完成的 Kulla-Conty BRDF 近似模型。完成 Kulla-Conty BRDF 模型,关键在于计算 BRDF 的补偿项 fms,而 fms的计算需要 E(µ) 和 Eavg 两个前置变量。由此本轮作业将分为以下两个部分:
- 在离线端 (lut-gen 文件夹中) 预计算 E(µ) 和 Eavg。
- 在实时端 (homework4 文件夹中) 通过查询预计算数据构建 BRDF 的补偿项。
首先我们来看一下结果图

上面一排是能量补全了的结果,下面一排是未经过能量补全的结果。可以很明显的看到,下面的模型是不太符合常理的,因为在我们的常识中,随着粗糙度的降低(从左到右),总体亮度不应该有太大的变化才对。所以我们需要对光照结果进行补全,得到上面第一排的那种符合我们认知的结果。
能量补全
为什么会出现能量损失
由于在实时渲染里面,只进行two bounces的计算,所以当粗糙度变得很高的时候,表面的自遮挡现象会很严重,导致了越来越多的光照被自身表面遮挡,需要数次弹射才能进入人的眼睛,所以两次弹射必定会出现一部分能量出不去的现象。粗糙度越高,只经过两次弹射损失的能量就会越多。

下面是白炉测试(通过在全局环境光作用下,不同粗糙度的物体反射得到的颜色可以直观的看出能量的损耗)

下面一排的小球是出于全局光照的小球,如果我们把它带入公式去计算,可以很明显的看到,小球越粗糙结果越暗。但是在现实世界里,如果在环境光恒为1的情况下,不管小球粗糙度是多少,我们看到的都应该是一个亮度为1的全白小球才对。所以只有当不同粗糙度下白炉测试都看不到球的情况才能说明能量是正确的。
如何进行能量补全
Kulla-Conty近似
Kulla-Conty近似以经验性的方式补全多次反射丢失的能量。
Kulla-Conty近似又分为两步
- 补全多次反射丢失的能量
- 还原有色物体该有的能量
补全多次反射丢失的能量
首先我们要考虑的是无色物体,根据上面的白炉测试,我们需要补全因为多次弹射而损失的能量,这里运用的主要是能量守恒的思想。
首先我们需要假设,入射光的radiance始终为1,也就是任何方向的光照都是1。当Li=1,则Lo等于只对F和Cos项进行积分。
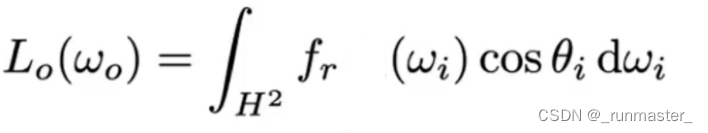
基于任何方向的光照都是1的假设,我们看到的每一个点的亮度也应该是1,所以在不考虑能量损失的情况下,任何一个点任意一个方向出射的总能量也应该是1。而我们知道Lo实际计算的是有能量损失的radiance/Irradiance(也就是求某个点吸收的所有方向的入射能量对某一个出射方向的影响),所以我们定义E(μo)就是μo方向有能量损失而剩下的能量。E(μo)的计算基于Li=1
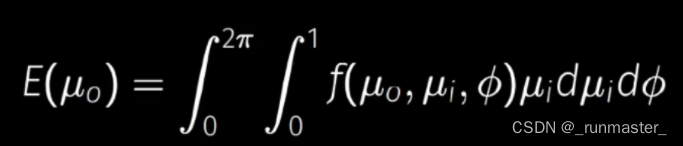
这里我们把dwi对单位立体角的积分拆解成了对单位φ和单位μ的积分,μ=sinθ,这里积分的拆解参考了知乎的一篇文章
所以我们需要补全的能量其实是1-E(μo),1-E(μo)是我们需要补全的总能量。我们知道了我们要补全的总能量了,但是现实情况是复杂的,补全的BRDF需要满足一些性质,因为入射光和出射光是可逆的,详细可以看这篇文章
我们需要把BRDF项写成
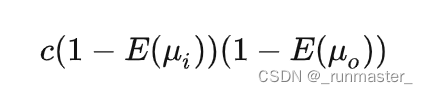
补充的Fms项的总能量是等于1-(μo)的

这边解得c=π(1-Eavg),Eavg=两倍E(μ)*μ对μ的积分。
这里还需要去求解Eavg,不过一旦求出了E(μ)以后,求Eavg就变得很轻松了。
预计算E(μo)
我们这里的目的就是求BRDF的补充项Fms,而Fms与E(μ)和Eavg有关,E(μ)是原始BRDF的积分,我们把BRDF个拆开可以发现,E(μ)积分结果只和菲涅尔项、粗糙度和入射角度有关。
参考OpenGL的IBL高光部分
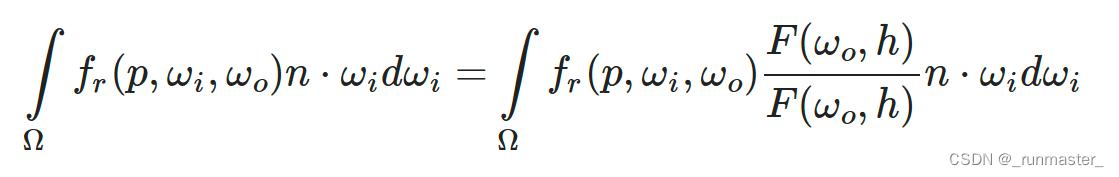
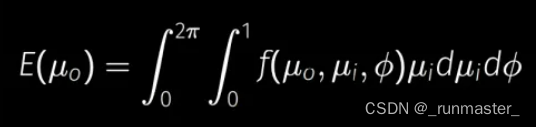
接下来我们开始预计算E(μ),首先我们先了解一下什么是split sum
split sum可以把多个函数的积分拆解成多个多个函数积分的积
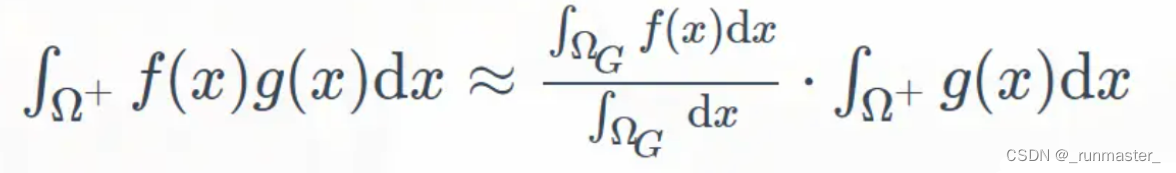
split sum是一种近似方式,要使split sum结果较为精确,那么需要满足以下一种或两种条件:
- 积分域 ΩG 比较小 (对应Specular的lobe很小)
- g(x)比较光滑,即变化不是很大 (对应Diffuse的fr变化不大) 于是渲染方程可以拆成两个部分分别进行求解(环境光积分、BRDF积分),后面会使用预计算的方法对两部分的计算分别进行优化。
split sum的意义在于将不可预计算的高维度积分拆解成多个低维度函数积分的乘积,预计算低维度函数的贴图,避免了需要高维空间存储预计算结果的麻烦。
- 不采用split sum
如果不采用split sum,我们已知E(μ)积分结果只和菲涅尔项、粗糙度和入射角度有关,那么就是有三个变量,需要一张三维贴图来存放预计算结果,代价比较大,所以我们把菲涅尔项用1来替代,简化计算
//Emu_MC.cpp
Vec3f IntegrateBRDF(Vec3f V, float roughness, float NdotV) {
float A = 0.0;
float B = 0.0;
float C = 0.0;
const int sample_count = 1024;
Vec3f N = Vec3f(0.0, 0.0, 1.0);
//对各个方向采样
samplePoints sampleList = squareToCosineHemisphere(sample_count);
for (int i = 0; i < sample_count; i++) {
// TODO: To calculate (fr * ni) / p_o here
Vec3f L = normalize(sampleList.directions[i]);
Vec3f H = normalize(V + L);
float Cos = std::max(dot(N, L), 0.0f);
float NdotL = Cos;
Vec3f F = Vec3f(1.0,1.0,1.0);
float NDF = DistributionGGX(N, H, roughness);
float G = GeometrySmith(roughness, NdotV, NdotL);
//这里的PDF是均匀的
float pdf=sampleList.PDFs[i];
float f = NDF * G * F.x / (4.0 * NdotV * NdotL)/pdf*Cos;
A = B = C += f;
}
//ABC分别是RGB3个通道,其实几个通道都没关系,因为他们记录的都是一个值
return {A / sample_count, B / sample_count, C / sample_count};
}

可以看到在粗糙度较低时,我们计算出的积分值非常小并且有很多噪声。这是因为低粗糙度的微表面材质接近镜面反射材质,即微表面的法线 m(即半程向量 h) 集中分布在几何法线 n 附近,而我们由采样入射光方向 i 计算出的微表面法向量 m 分布并不会集中在几何法线 n 附近,也就是说这与实际低粗糙度的微表面法线分布相差很大,因此积分值的方差就会很大。实际上,我们可以通过对微表面法线 m 进行重要性采样来改善这个一问题,这部分属于本次作业的提高部分。
- 采用split sum + 重要性采样
如果采用split sum方法,我们可以那菲涅尔项提出来,这里用的是split的分割思想,尽量消除F对式子的影响,只关注粗糙度和入射角度两个变量

F为菲涅耳方程。将菲涅耳分母移到 BRDF 下面可以得到如下等式:
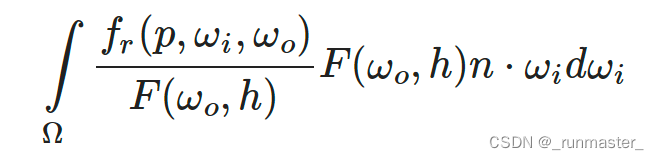
用 Fresnel-Schlick 近似公式替换右边的 F 可以得到:
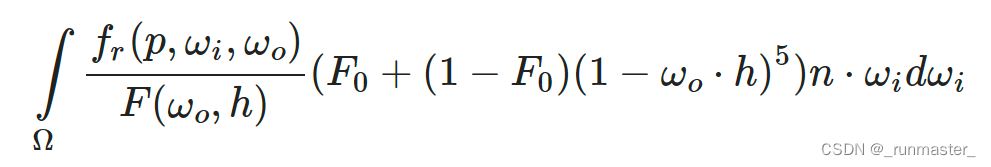
用α替换(1-wo*h)^5
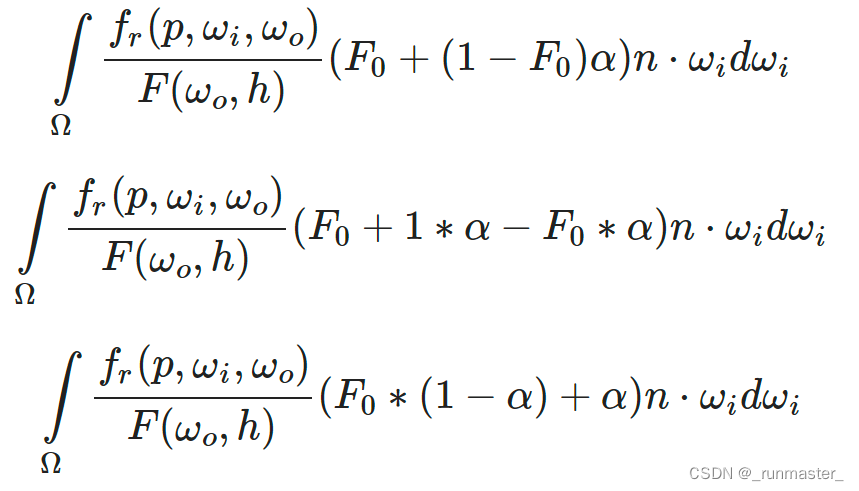
然后我们将菲涅耳函数F分拆到两个积分里:
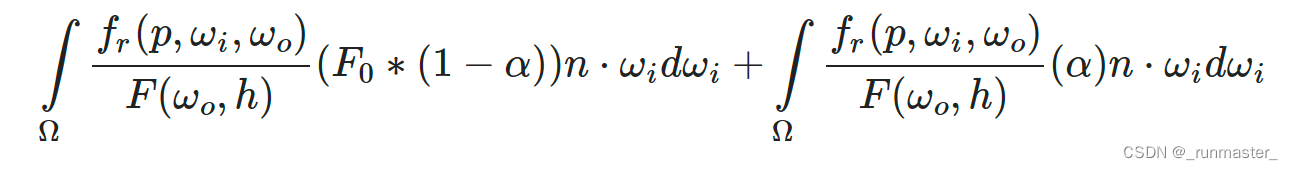
还原一下就是

我们把F提出来了,替换成了用F0表示,因此我们只需要预计算关于粗糙度和入射角度的二维贴图即可。
在做到这一步,我们顺便实现一下作业中的提高项,在此中加入重要性采样。
我们可以参照Eavg_MC.cpp中的GeometrySchlickGGX把Emu_IS.cpp的GeometrySchlickGGX实现出来。
//Emu_IS.cpp
float GeometrySchlickGGX(float NdotV, float roughness) {
// TODO: To calculate Schlick G1 here - Bonus 1
float a = roughness;
float k = (a * a) / 2.0f;
float nom = NdotV;
float denom = NdotV * (1.0f - k) + k;
return nom / denom;
}
关于ImportanceSampleGGX和其中使用的Hammersley生成低差异序列的方法,我们可以参考LearnOpenGL的IBL部分
//Emu_IS.cpp
Vec3f ImportanceSampleGGX(Vec2f Xi, Vec3f N, float roughness) {
float a = roughness * roughness;
//TODO: in spherical space - Bonus 1
float theta = atan(a * sqrt(Xi.x) / sqrt(1.0f - Xi.x));
float phi = 2.0 * PI * Xi.y;
//TODO: from spherical space to cartesian space - Bonus 1
float sinTheta = sin(theta);
float consTheta = cos(theta);
Vec3f H = Vec3f(cos(phi) * sinTheta, sin(phi) * sinTheta, consTheta);
//TODO: tangent coordinates - Bonus 1
Vec3f up = abs(N.z) < 0.999 ? Vec3f(0.0, 0.0, 1.0) : Vec3f(1.0, 0.0, 0.0);
Vec3f tangent = normalize(cross(up, N));
Vec3f bitangent = cross(N, tangent);
//TODO: transform H to tangent space - Bonus 1
Vec3f sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
return normalize(sampleVec);
}
引入了重要性采样以后,我们结合split sum进行预计算,首先我们要搞清楚,重要性采样是根据入射方向和粗糙度返回一个采样方向,所以我们用H半程向量接受重要性采样得到的结果来进行采样。而我们计算的E(μ)其实还包含了除pdf这个操作
最终得到的结果如下
Fms=F0∫fr(1-(1-wo*h)^5)/pdf*n*widwi+∫fr(1-wo*h)^5/pdf*n*widwi
我们把式子fr/pdf化简
参考这篇文章

对BRDF的计算可以转化成菲涅尔项F乘权重Weight,而我们把对菲涅尔项的计算放到实时计算部分,目前我们只进行预计算,所以我们只算Weight项就可以了,但根据下面公式
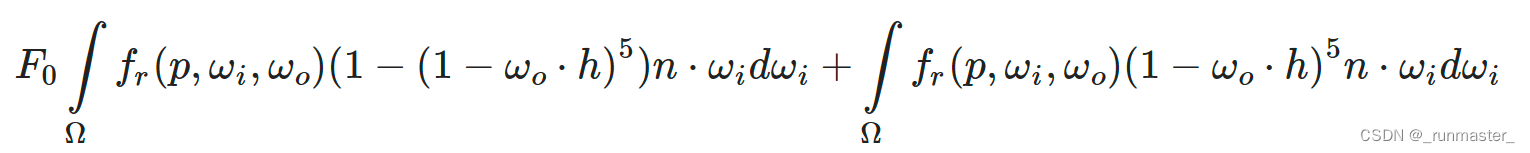
我们对菲涅尔项的处理可以拆成F0的形式,而为了加快速度,我们可以把原本菲涅尔项的(1-woh) ^5拆分到预计算部分一起计算,我们设α= (1-woh) ^5
//Emu_IS.cpp
Vec3f IntegrateBRDF(Vec3f V, float roughness) {
const int sample_count = 1024;
float Emu1=0.0f;
float Emu2=0.0f;
Vec3f N = Vec3f(0.0, 0.0, 1.0);
for (int i = 0; i < sample_count; i++) {
Vec2f Xi = Hammersley(i, sample_count);
Vec3f H = ImportanceSampleGGX(Xi, N, roughness);
Vec3f L = normalize(H * 2.0f * dot(V, H) - V);
float NoL = std::max(L.z, 0.0f);
float NoH = std::max(H.z, 0.0f);
float VoH = std::max(dot(V, H), 0.0f);
float NoV = std::max(dot(N, V), 0.0f);
// TODO: To calculate (fr * ni) / p_o here - Bonus 1
//提出实时计算中菲涅尔项F中的部分信息,用α表示
float a = pow(1.0f - VoH, 5.0f);
//计算weight
float G= GeometrySmith(roughness, NoV, NoL);
float weight = VoH * G / (NoV * NoH);
Emu1 += (1-a) * weight;
Emu2 += a* weight;
// Split Sum - Bonus 2
}
//用R、G两通道存储带F0的BRDF和不带F0的
return Vec3f(Emu1 / sample_count, Emu2 / sample_count,0.0);
}
上面公式我们计算了weight以及从实时计算部分拆出来的α项,然后分别把下面两部分积分用R、和G两个通道进行存储
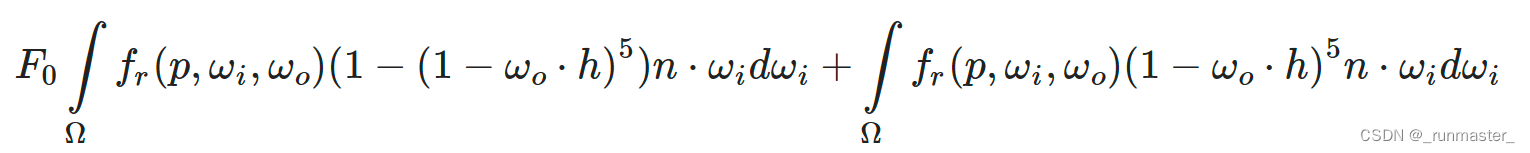
得到图片结果
预计算Eavg
根据公式,我们通过已计算出的E(μ)来求Eavg
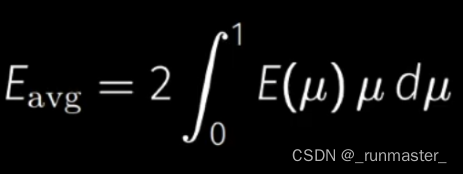
公式里需要我们对E(μ)进行积分,但是作业框架里面,在给定了NdotV也就是μ的2情况下,他在函数内部又进行了采样,实际上是不需要这样的,因为上面公式可知,Eavg的结果跟E(μ)*μ的积分有关,而函数传入的参数包含了E(μ)和μ,也就是说如果不改变E(μ)和μ的值,采样对最终结果是没什么影响的。
Vec3f IntegrateEmu(Vec3f V, float roughness, float NdotV, Vec3f Ei) {
Vec3f Eavg = Vec3f(0.0f);
const int sample_count = 1024;
Vec3f N = Vec3f(0.0, 0.0, 1.0);
samplePoints sampleList = squareToCosineHemisphere(sample_count);
//采样并不会改变Eavg的结果,因为采样不会影响Ei * NdotV的值,这是函数参数传入的
for (int i = 0; i < sample_count; i++) {
Vec3f L = sampleList.directions[i];
Vec3f H = normalize(V + L);
float NoL = std::max(L.z, 0.0f);
float NoH = std::max(H.z, 0.0f);
float VoH = std::max(dot(V, H), 0.0f);
float NoV = std::max(dot(N, V), 0.0f);
// TODO: To calculate Eavg here
Eavg += Ei * NdotV * 2;
}
return Eavg / sample_count;
}
得到结果

还原有色物体该有的能量
还原有色物体该有的能量这一步我们在实时渲染里面完成
首先我们先把我们在离线端生成的GGX_E_LUT.png和GGX_Eavg_LUT.png拷贝到实时渲染端下的assets/ball目录下。
把engine.js脚本下的两行代码取消注释了,不然会少了roughness为0.15的模型展示
/engine.js
//..
loadGLTF(renderer, 'assets/ball/', 'ball', 'KullaContyMaterial', Sphere0Transform, metallic, 0.15);
//..
loadGLTF(renderer, 'assets/ball/', 'ball', 'PBRMaterial', Sphere5Transform, metallic, 0.15);
接着我们需要在PBRFragment.glsl,KullaContyFragment.glsl内补全计算BRDF用的NDF、G和F函数
//PBRFragment.glsl、KullaContyFragment.glsl
float DistributionGGX(vec3 N, vec3 H, float roughness)
{
// TODO: To calculate GGX NDF here
float a = roughness*roughness;
float a2 = a*a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH*NdotH;
float nom = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return nom / max(denom, 0.0001);
}
float GeometrySchlickGGX(float NdotV, float roughness)
{
// TODO: To calculate Smith G1 here
float a = roughness;
float k = (a * a) / 2.0;
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
// TODO: To calculate Smith G here
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx2 = GeometrySchlickGGX(NdotV, roughness);
float ggx1 = GeometrySchlickGGX(NdotL, roughness);
return ggx1 * ggx2;
}
vec3 fresnelSchlick(vec3 F0, vec3 V, vec3 H)
{
// TODO: To calculate Schlick F here
return F0 + (1.0 - F0) * pow(clamp(1.0 - max(dot(H, V), 0.0), 0.0, 1.0), 5.0);
}
补充完上面的函数我们可以得到以下效果

上面一排是还没完善的KullaConty的着色模型,下面的是有明显能量损失的着色模型。
我们要对BRDF项进行补全,最终得到的能量守恒的Kulla-Conty材质的BRDF项应该为:
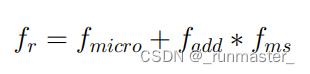
fmicro是原BRDF项,fadd是还原颜色的BRDF项,fms是补充能量损失的BRDF项。
fms在补全能量损失的那一步讲过他的计算原理
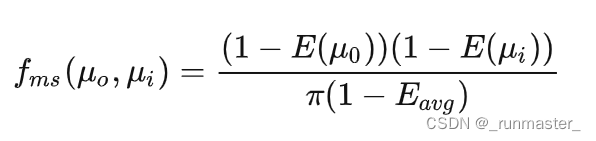
现在我们来了解一下如何还原颜色项fadd。
在上一步补全多次反射丢失的能量中,由于物体没有颜色,F项默认是(1,1,1)。而人之所以能看到颜色,是因为物体反射了颜色,而光是白色的,除了人眼看到的颜色,其他的颜色会被物体表面吸收,所以只要是有色物体,就一定存在能量损失。该方法可以通过先补全多次反射丢失的能量,再在此基础上还原有色物体的该有的能量来得到基于物理的效果。
首先先计算Favg,用一个平均值取代由不同观察角度得到的反射率。相比于基于真实物理的方法,这样的hack可以大幅度减少计算量,又能得到相差无几的效果。
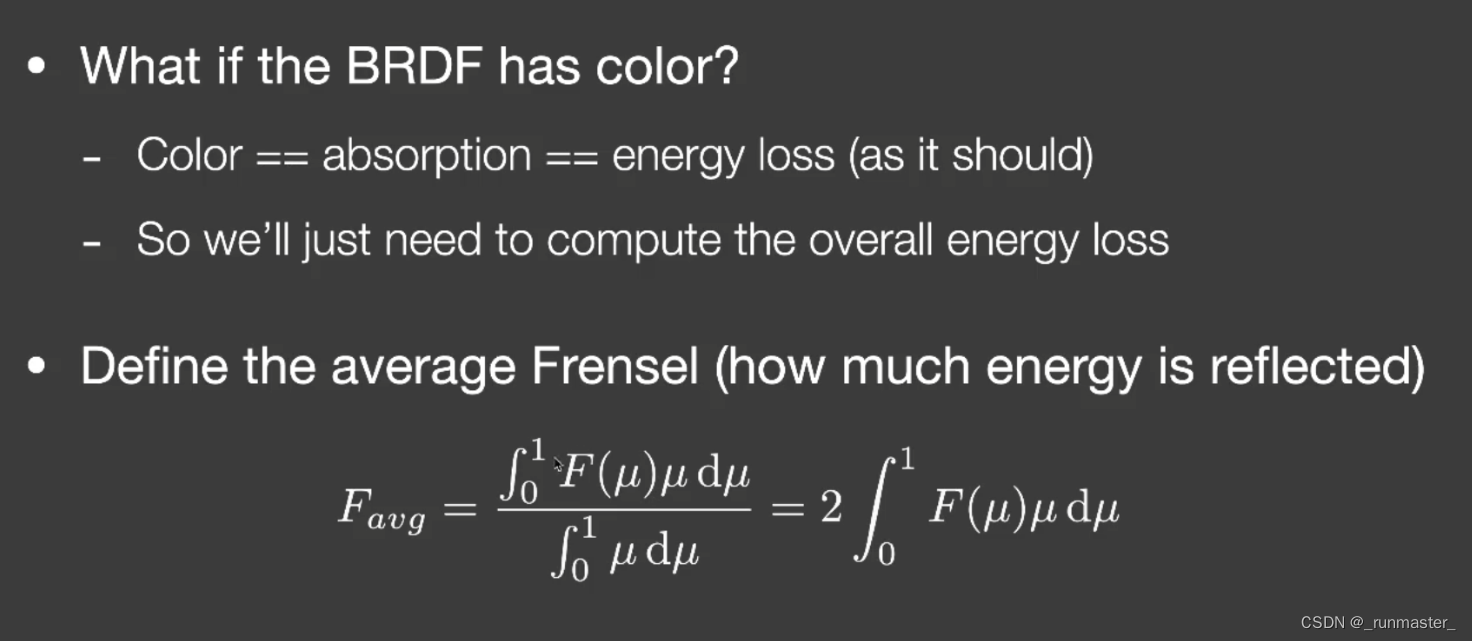
下面开始计算有色物体反射的能量率
Favg*Eavg可以得到对直接光能量的反射率
(1-Eavg)代表了由于自遮挡被表面挡住的能量,Favg*(1-Eavg)代表了有色物体真正反射出去由于自遮挡被表面挡住的能量
Favg(1-Eavg)Favg*Eavg则代表了有色物体反射出去却被表面挡住的能量二次反射到人眼的真实能量
以此类推,当把k 次bounds的能量都加上的时候就是真实还原的能量效率了

在补全多次反射丢失的能量后再还原该有色物体该有的能量后,我们应该可以观察到以下效果

所以我们得出计算fadd的公式
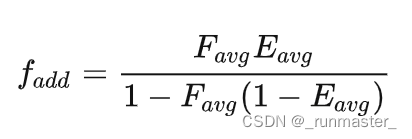
作业框架直接为我们提供了计算Favg的函数AverageFresnel(albedo, edgetint),我们直接计算便可。
由于我们需要在实时计算过程中加入F0,因此我们需要对作业中的MultiScatterBRDF函数进行重载
//KullaContyFragment.glsl
vec3 MultiScatterBRDF(float NdotL, float NdotV)
{
vec3 albedo = pow(texture2D(uAlbedoMap, vTextureCoord).rgb, vec3(2.2));
vec3 E_o = texture2D(uBRDFLut, vec2(NdotL, uRoughness)).xyz;
vec3 E_i = texture2D(uBRDFLut, vec2(NdotV, uRoughness)).xyz;
vec3 E_avg = texture2D(uEavgLut, vec2(0, uRoughness)).xyz;
// copper
vec3 edgetint = vec3(0.827, 0.792, 0.678);
vec3 F_avg = AverageFresnel(albedo, edgetint);
// TODO: To calculate fms and missing energy here
vec3 F_ms = (1.0 - E_o) * (1.0 - E_i) / (PI * (1.0 - E_avg));
vec3 F_add = F_avg * E_avg / (1.0 - F_avg * (1.0 - E_avg));
return F_add * F_ms;
}
vec3 MultiScatterBRDF(float NdotL, float NdotV, vec3 F0)
{
vec3 albedo = pow(texture2D(uAlbedoMap, vTextureCoord).rgb, vec3(2.2));
// A split-sum result in which R-channel repesent F0 interger term
vec3 E_o = texture2D(uBRDFLut, vec2(NdotL, uRoughness)).xyz;
vec3 E_i = texture2D(uBRDFLut, vec2(NdotV, uRoughness)).xyz;
// Split sum result add here.
vec3 Emu_o = F0 * E_o.x + vec3(1.0) * E_o.y;
vec3 Emu_i = F0 * E_i.x + vec3(1.0) * E_i.y;
vec3 E_avg = texture2D(uEavgLut, vec2(0, uRoughness)).xyz;
vec3 E_avgss = F0 * E_avg.x + vec3(1.0) * E_avg.y;
// copper
vec3 edgetint = vec3(0.827, 0.792, 0.678);
vec3 F_avg = AverageFresnel(albedo, edgetint);
// TODO: To calculate fms and missing energy here
vec3 F_ms = (1.0 - Emu_o) * (1.0 - Emu_i) / (PI * (1.0 - E_avgss));
vec3 F_add = F_avg * E_avgss / (1.0 - F_avg * (1.0 - E_avgss));
return F_ms * F_add;
}
上面的不带F0参数的用于非split sum的计算,而带F0参数的用来计算带有重要性采样+split sum的
按需求修改main里的函数
//KullaContyFragment.glsl
//..
vec3 F0 = vec3(0.04);
F0 = mix(F0, albedo, uMetallic);
//..
vec3 Fms = MultiScatterBRDF(NdotL, NdotV, F0);
//vec3 Fms = MultiScatterBRDF(NdotL, NdotV);
没有split sum的结果

重要性采样+split sum的结果

参考文章:
GAMES202-作业4:Kulla-Conty BRDF
镜面反射 IBL
GGX重要性采样
蒙特卡洛积分


