梯度下降法预测波士顿房价问题

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

下面是一个梯度下降法对多元问题的求解：

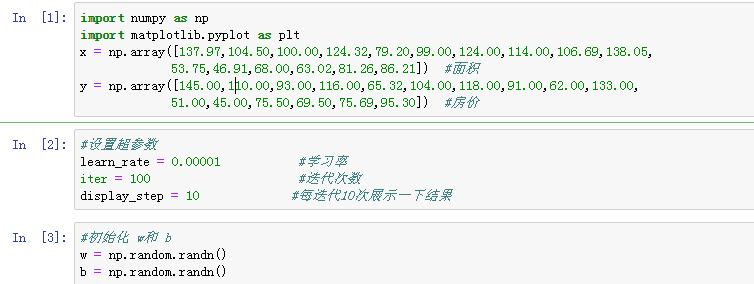
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Simhei']

area = np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,
             53.75,46.91,68.00,63.02,81.26,86.21])             #面积
room = np.array([3,2,2,3,1,2,3,2,2,3,1,1,1,1,2,2])              #房间数
price = np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,
             51.00,45.00,75.50,69.50,75.69,95.30])              #房价
num = len(area)
x0 = np.ones(num)
x1 = (area - area.min())/(area.max() - area.min())           #对房间面积进行标准化
x2 = (room - room.min())/(room.max() - room.min())            #对房间数进行标准化

X = np.stack((x0,x1,x2), axis = 1)
Y = price.reshape(-1,1)

#设置超参数
learn_rate = 0.001
iter = 500
display_step = 50

#初始化w
np.random.seed(612)
W = np.random.randn(3,1)

 

 

#训练模型
mse = []
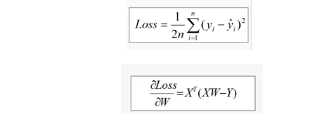
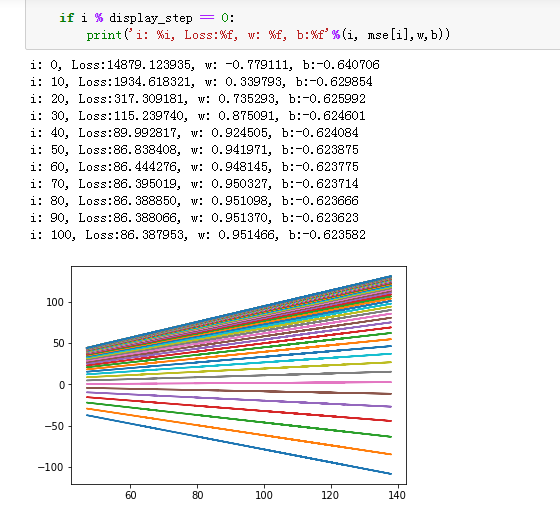
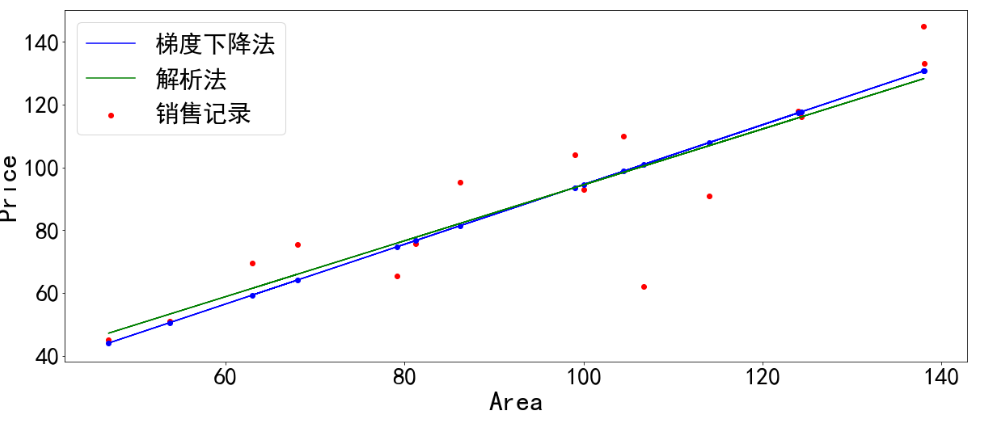
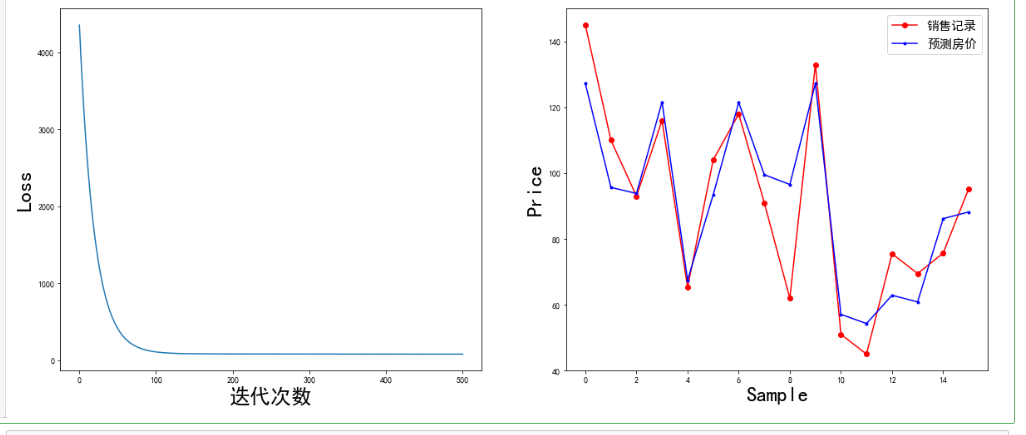
for i in range(iter+1):
    dL_dw = np.matmul(np.transpose(X),np.matmul(X,W)-Y)    #对W的偏导
    W = W-learn_rate*dL_dw                   #更新权值
    
    PREDIC = np.matmul(X,W)                 #房价估计值
    Loss = np.mean(np.square(Y-PREDIC))/2
    mse.append(Loss)
    
    if i % display_step ==0:
        print('i: %i, Loss:%f'%(i,mse[i]))
        
#可视化结果
plt.figure(figsize=(20,8))

plt.subplot(1,2,1)
plt.plot(mse)
plt.xlabel('迭代次数', fontsize = 25)
plt.ylabel('Loss', fontsize = 25)

plt.subplot(1,2,2)
PREDIC = PREDIC.reshape(-1)
plt.plot(price,color = 'red', marker = 'o', label = '销售记录')
plt.plot(PREDIC, color = 'blue', marker = '.', label='预测房价')
plt.xlabel('Sample', fontsize = 25)
plt.ylabel('Price', fontsize=25)

plt.legend(fontsize=15)
plt.show()