机器学习之线性回归

回归是统计学中最有力的工具之一。机器学习监督学习算法分为分类算法和回归算法两种，其实就是根据类别标签分布类型为离散型、连续性而定义的。回归算法用于连续型分布预测，针对的是数值型的样本，使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

因此线性回归可以被定义为：通过一个或者多个自变量与因变量之间进行建模的回归分析。

 

 

 比如预测房子价格，可以通过房子的面积一个变量来预测，也可以根据面积和位置来预测。

 

 

 

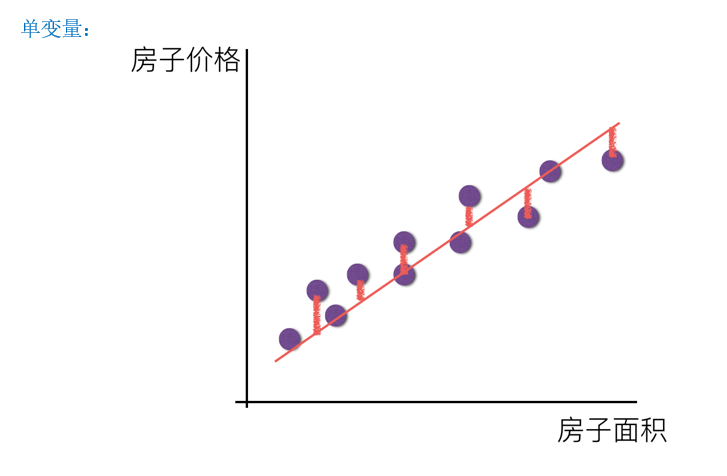
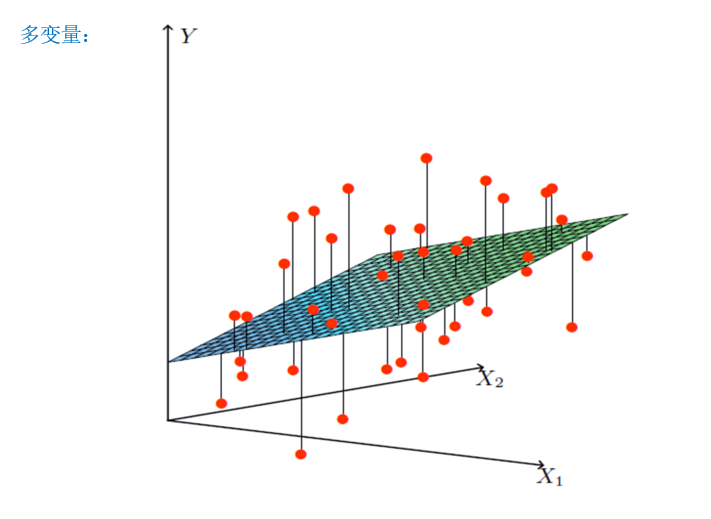
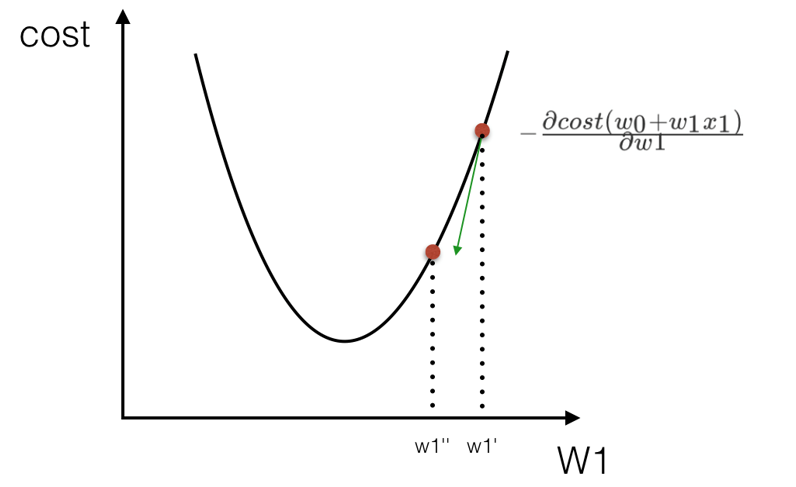
从上面两张图种可以看出，无论怎么构建这个回归模型，总会存在误差，也就是说总会有一些点没有落在建立的线或者面上面。真实值与预测值之间的差距就叫做误差大小，也叫做损失函数。

而我们建立回归模型的目的之一，就是尽可能的将这个损失函数的值降到最低，也就是要找到最佳的权重w。

 

 

 寻找最佳的权重w，有两种方法：

第一：正规方程

 

 

 第二：梯度下降

 

 

 

 

 

 

 

 -------------------------------------------------------------------------------------------------------------------

正规方程API：sklearn.linear_model.LinearRegression

• coef_:是最优的回归系数

梯度下降API：sklearn.linear_model.SGDRegressor

•  coef_:是最优的回归系数

 

以波士顿房价数据预测为例：

 

 因为变量都涉及到一个权重，所以需要对每一个变量都要进行数据标准化处理，否则会出现 “大数吃小数” 现象。

了解一下数据集：

 

 

上代码（正规方程）：

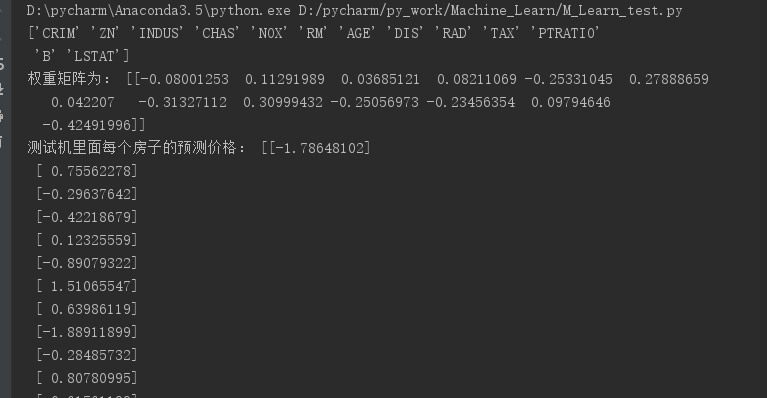
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

def myliner():
    '''
    线性回归直接预测房子价格
    :return: None
    '''
    #获取数据
    lb = load_boston()
    print(lb.get('feature_names'))

    #分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data,lb.target,test_size=0.25)

    #进行标准化处理
    #特征值和目标值都必须进行标准化处理，实例化两个标准化API

    # 特征值
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    #目标值
    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train.reshape(-1,1)) #sklearn0.19版本要求目标值必须为二维向量，因此这里需要转换为二维的
    y_test = std_y.transform(y_test.reshape(-1,1))

    #estimator预测
    lr = LinearRegression()
    lr.fit(x_train,y_train)

    print('权重矩阵为：',lr.coef_)

    #预测测试集的房子价格
    y_predict = lr.predict(x_test)
    print('测试机里面每个房子的预测价格：',y_predict)

    return None


if __name__ == '__main__':
    myliner()

结果（正规方程）：

 

 

上代码(梯度下降)：

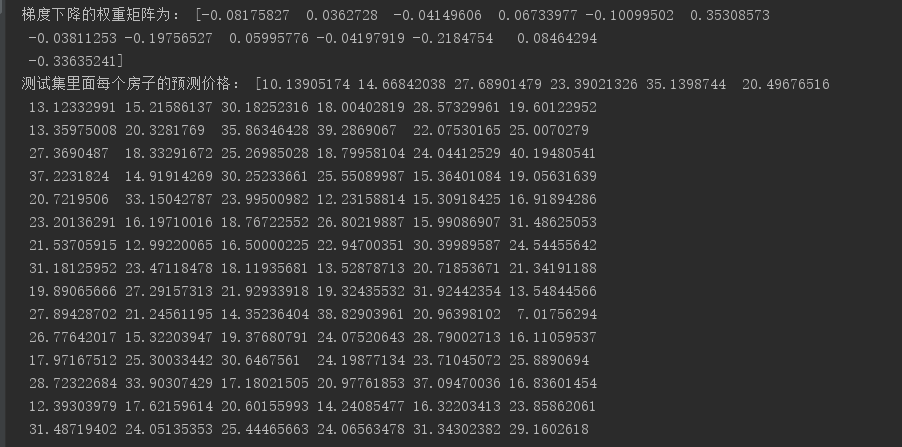
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

def myliner():
    '''
    线性回归直接预测房子价格
    :return: None
    '''
    #获取数据
    lb = load_boston()
    print(lb.get('feature_names'))

    #分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data,lb.target,test_size=0.25)

    #进行标准化处理
    #特征值和目标值都必须进行标准化处理，实例化两个标准化API

    # 特征值
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    #目标值
    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train.reshape(-1,1)) #sklearn0.19版本要求目标值必须为二维向量，因此这里需要转换为二维的
    y_test = std_y.transform(y_test.reshape(-1,1))

    #梯度下降进行房价预测
    sgd = SGDRegressor()

    sgd.fit(x_train,y_train)
    print("梯度下降的权重矩阵为：", sgd.coef_)
    #预测测试集的房子价格
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
    print('测试集里面每个房子的预测价格：',y_sgd_predict)

    return None


if __name__ == '__main__':
    myliner()

结果：

 

 

回归性能的评估：

对于不同的类别预测，我们不能苛刻的要求回归预测的数值结果要严格的与真实值相同。一般情况下，我们希望衡量预测值与真实值之间的差距。因此，可以测评函数进行评价。其中最为直观的评价指标均方误差(Mean Squared Error)MSE，因为这也是线性回归模型所要优化的目标。MSE的计算方法如下：

 

 

 API：sklearn.metrics.mean_squared_error

 

 上代码:

from sklearn.metrics import mean_squared_error

print('正规方程的均方误差：',mean_squared_error(std_y.inverse_transform(y_test),y_lr_predict))

print('梯度下降的均方误差：', mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))

结果:

 

 

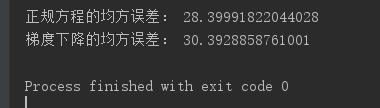
从结果可以看出，虽然正规方程法的适用性比较小，但是在一些数据集的预测种其准确也有可能优于梯度下降。

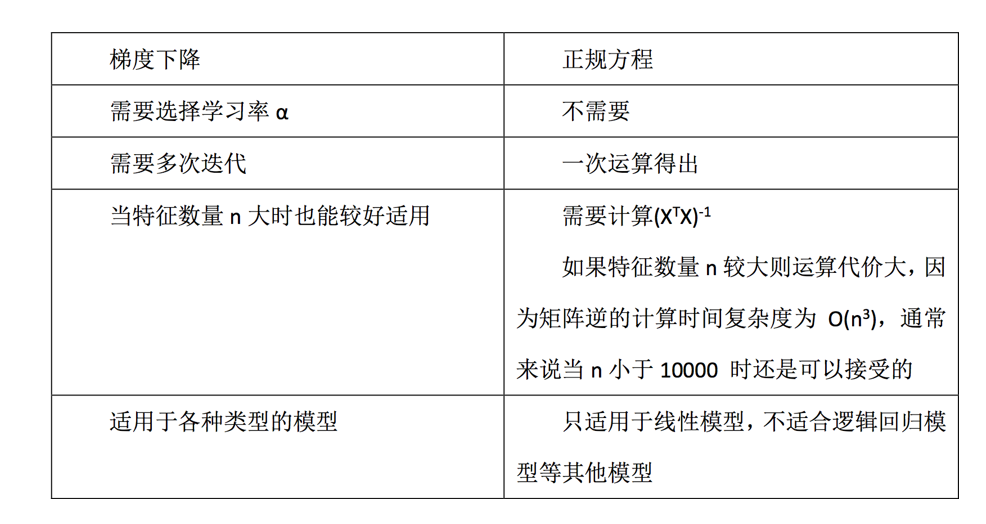
一般来说，梯度下降法更适用于大数据集的预测。二者的组要区别如下：