P1028 数的计算

题目连接

题面：

 

思路:

拿n = 17举个例子：

首先 17 肯定是答案之一  ， ans = 1;

第二位可以放 1 ~ 8（构成117 、217 、 317 等等）, ans = 1 + 8 = 9：

 

 

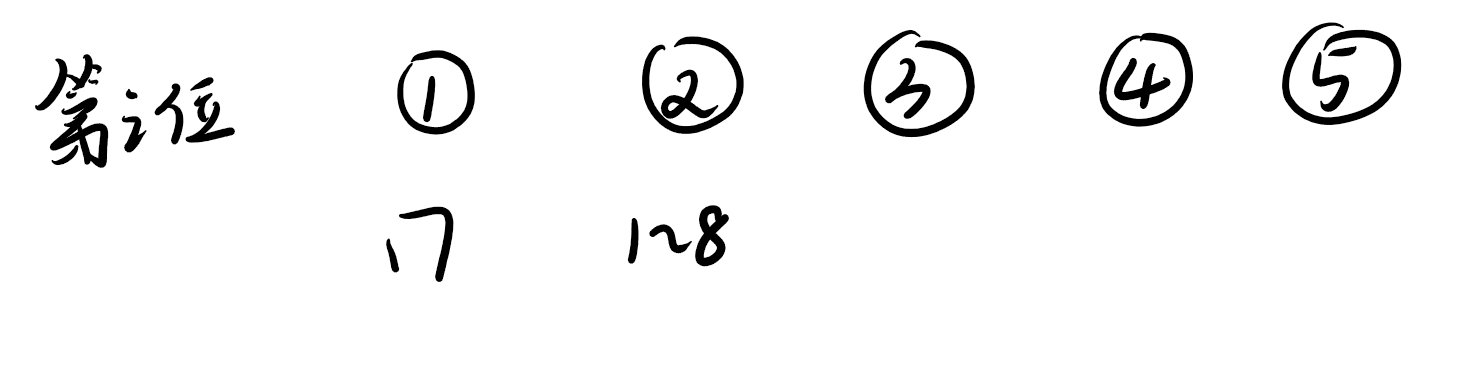
第三位可以放 1 ~ 4 ，但只能放特定的位置：

　　比如我在第三位放 1 ，那么第二位是能是 2 ~ 8 

　　比如我在第三位放 3 ，那么第二位是能是 6 ~ 8 

　　

 

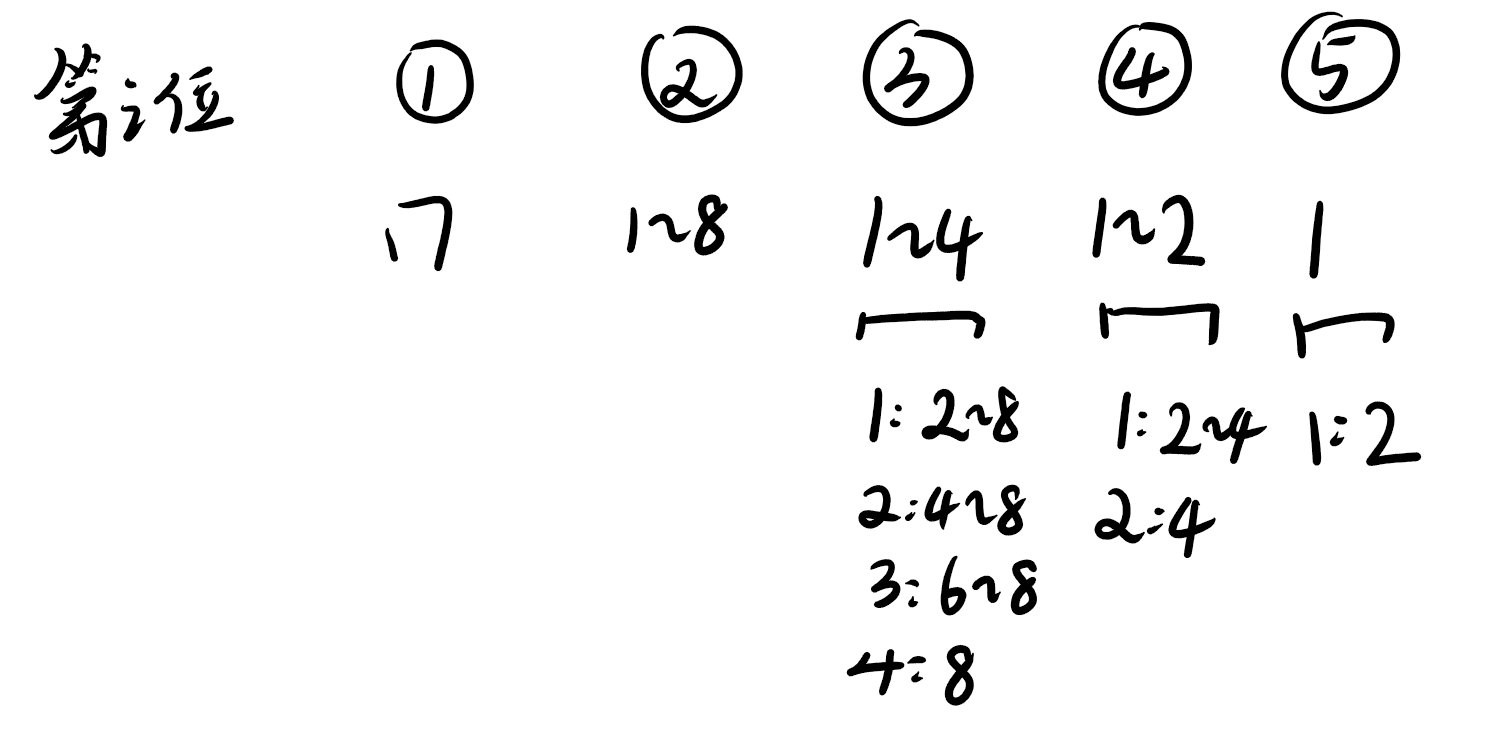
比如我在第四位放 1 ，那么第三位只能是 2 ~ 4 , 满足第三位是 2 ~ 4 的情况有 （8 - 4 + 1） + （8 - 6 + 1） + （8 - 8 + 1） = 9 种 ， 所以最后一位为第四位且是1的情况数有 9种 

所以每次把当前位当成最后一位，算以j结尾的情况数。

代码:

#include<bits/stdc++.h>
using namespace std;
const int maxn =  1e6 + 10;
#define ll long long
#define ios std::ios::sync_with_stdio(false)
#define int long long
int num[maxn];
int nex[maxn];
signed main()
{
    ios;
    cin.tie(0);
    int n;
    cin >> n;
    int up = n / 2;
    int ans = 1 + n / 2;
    for(int i = 1 ; i <= n / 2 ; i ++){
        num[i] = 1;
    }
    while(up / 2 >= 1){
        nex[up + 1] = 0;
        for(int i = up ; i >= 1 ; i --){
            nex[i] = nex[i + 1] + num[i];
        }
        for(int i = 1 ; i <= up / 2 ; i ++){
            num[i] = nex[2 * i];
            ans += num[i];
        }
        up /= 2;
    }
    cout << ans << '\n';
    return 0;
}