【LeetCode每天一题】Edit Distance(编辑距离)
Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.You have the following 3 operations permitted on a word:
- Insert a character
- Delete a character
- Replace a character
Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
思路
这道题是一道典型的使用动态规划来解决的题目。两个单词我们申请一个(m+1)*(n+1)的矩阵,首先对矩阵的第一行和第一列进行初始化,然后从第二行第二个位置开始进行遍历,每次得到最小的编辑数。 这里如果当前两个字母相等的话,直接使其等于上一个字母的编辑数,也即dp[i][j] = dp[i-1][j-1]。但是当两个字母不相等的时候,我们可以从左边上边和右上角选出最小的编辑数在加一,得到当前位置的编辑数,也即dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1]))+1。这样直到循环遍历到矩阵的末尾。最后一个数字也即是最小编辑距离。时间复杂度为O(m*n),空间复杂度为O(m*n)。
一般对于动态规划来题目来说,我们除了设置一个(m+1)*(n+1)的矩阵外,还可以使用(n+1)大小的矩阵。这里动态方程还是一样的,只不过这里我们需要处理的细节更多一些。时间复杂度和上面的一样,空间复杂度为O(n+1)。
图示步骤
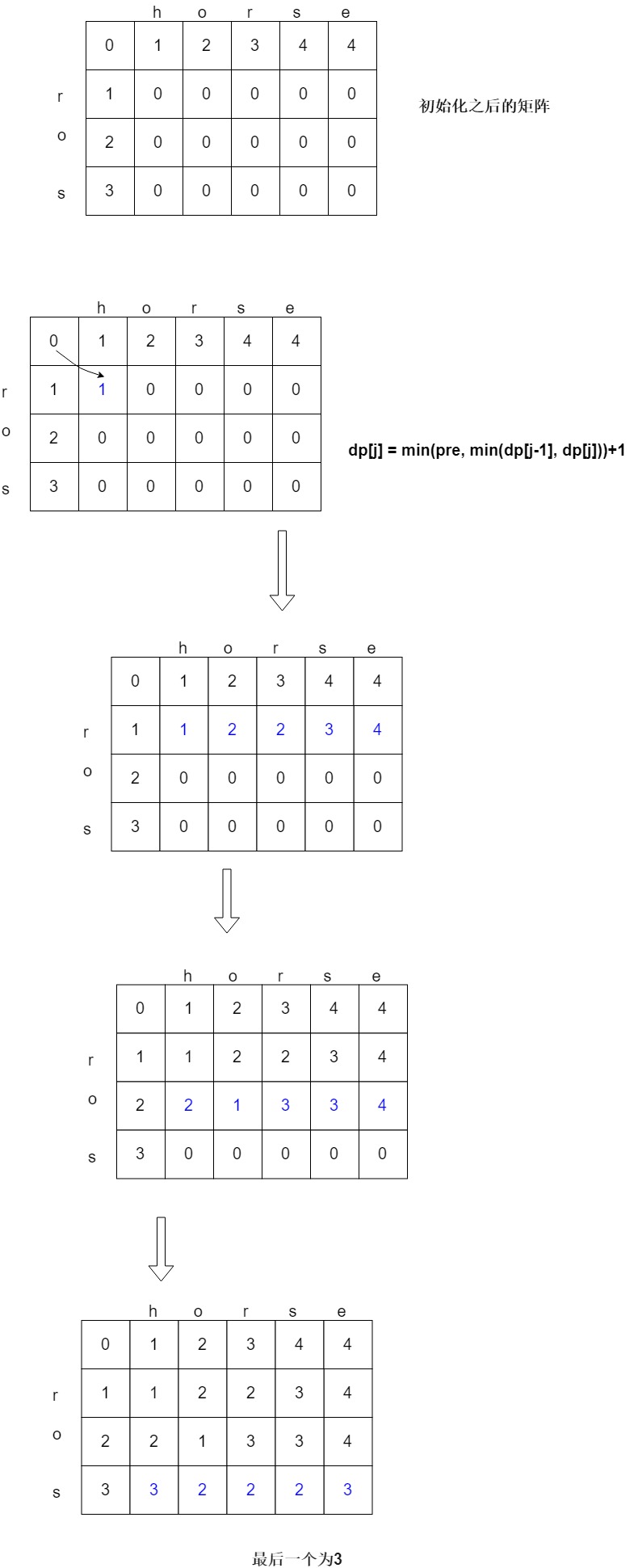 解决代码
解决代码
第一种空间复杂度为O(m*n)的解法
1 class Solution(object):
2 def minDistance(self, word1, word2):
3 """
4 :type word1: str
5 :type word2: str
6 :rtype: int
7 """
8 if not word1 or not word2: # 一个为空直接返回另一个不为空的长度。
9 return len(word1) if not word2 else len(word2)
10
11 m, n= len(word1), len(word2)
12 dp = []
13 for i in range(m+1): # 构造辅助矩阵
14 dp.append([0]*(n+1))
15
16 for i in range(1, m+1): # 初始化第一列
17 dp[i][0] = i
18
19 for j in range(1, n+1): # 初始化第一行
20 dp[0][j] = j
21
22 for i in range(1, m+1): # 逐个求解
23 for j in range(1, n+1):
24 if word1[i-1] == word2[j-1]: # 当前字母相等时,
25 dp[i][j] = dp[i-1][j-1]
26 else: # 不相等时
27 dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1]))+1
28 return dp[m][n]
空间复杂度为O(n)的解法
1 class Solution(object):
2 def minDistance(self, word1, word2):
3 """
4 :type word1: str
5 :type word2: str
6 :rtype: int
7 """
8 if not word1 or not word2:
9 return len(word1) if not word2 else len(word2)
10 m, n= len(word1), len(word2)
11 dp = [0]*(n+1) # 申请辅助数据
13 for i in range(1, n+1): # 初始化第一行
14 dp[i] = i
15
16 for i in range(1,m+1): # 循环遍历
17 pre = dp[0] # 记录下dp[0]的值,也即为上面矩阵中dp[i-1][j-1]的值。
18 dp[0]= i # 给dp[0]赋值为当前单词编辑列的距离,也就是上面的初始化第一列
19 for j in range(1, n+1):
20 tem = dp[j] # 相当于记录下dp[i][j-1]的值,
21 if word1[i-1] == word2[j-1]: # 单词相等的时候
22 dp[j] = pre
23 else:
24 dp[j] = min(pre, min(dp[j-1], dp[j]))+1
25 pre = tem # 更新值
26
27 return dp[-1]
28



