【算法】堆排序
堆排序的时间复杂度和快排的平均时间复杂度一样为O(n log n)。其排序过程我们可以分为两个阶段一个就是建堆、另一个是排序。
建堆
对于建堆的办法有两种一种是像堆的插入操作一样,自下而上进行堆化。我们先假设堆中只有一个数据,然后此次插入到尾部进行堆化,当最后一个元素插入完毕并堆化之后就完成堆化。另外一种办法就是从非叶子节点开始(因为叶子节点没有子节点)进行从上往下堆化。当执行完毕到第一个节点之后就完成堆化。
如图所示
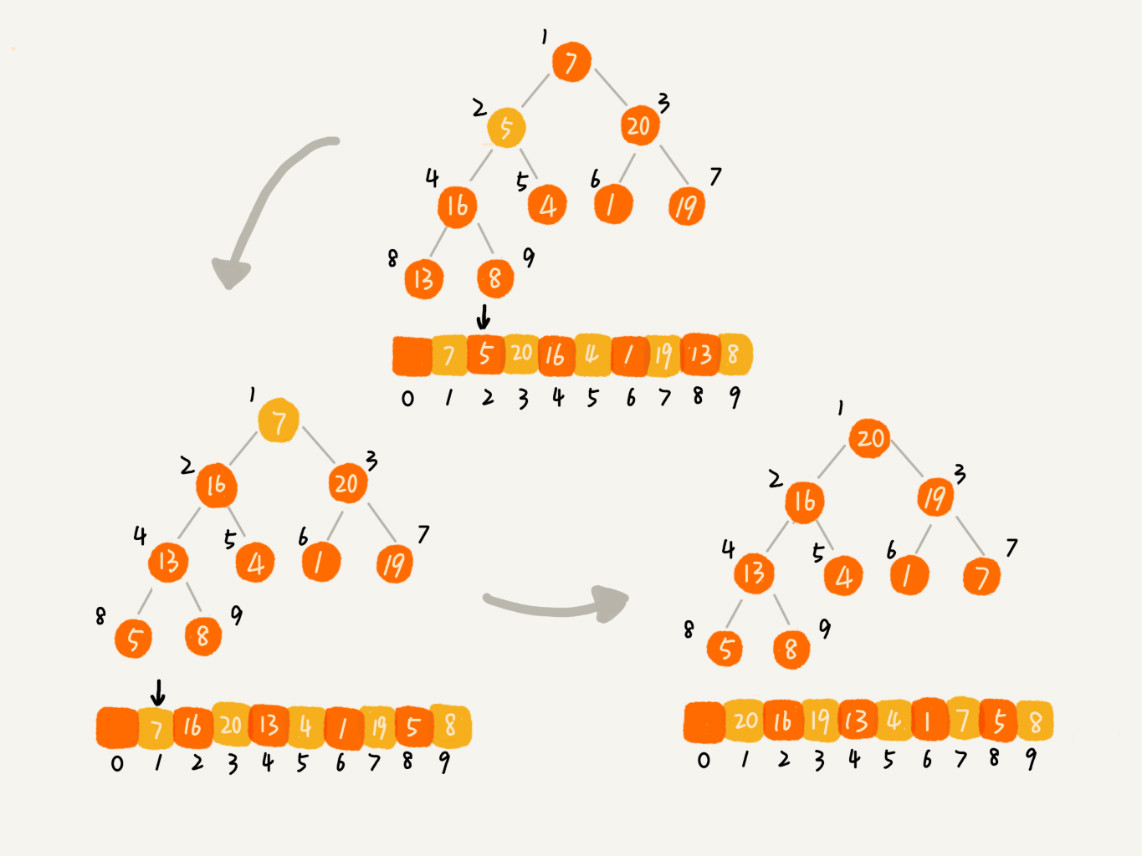
实现代码(可以发现和堆的删除操作代码一样, 因为都是从上而下进行堆化)
1 def buildheap(self):
2 index = self.count//2
3 while index >= 1:
4 while True:
5 maxpos = index
6 if index*2 <= self.count and self.a[index] < self.a[index*2]: # 找出子节点中最大的值的进行交换
7 maxpos = index
8 if index * 2+1 <= self.count and self.a[maxpos] < self.a[index*2+1]:
9 maxpos = index*2+1
10 if maxpos == index:
11 break
12 self.a[maxpos], self.a[index] = self.a[index], self.a[maxpos]
13 index = maxpos
堆化的时间复杂度为O(n)(精确一点),也可以是O(nlog n)。
堆排序
建堆结束之后,数组中的数据已经是按照大顶堆的特性来组织的。数组中的第一个元素就是堆顶,也就是最大的元素。我们把它跟最后一个元素交换,那最大元素就放到了下标为n的位置。这个过程有点类似删除堆顶元素的操作,当堆顶元素移除之后,我们把下标为n的元素放到堆顶,然后再通过堆化的方法,将剩下的n-1个元素重新构建成堆。堆化完成之后,我们再取堆顶的元素,放到下标n-1的位置。直到所有元素都完毕。
如图所示
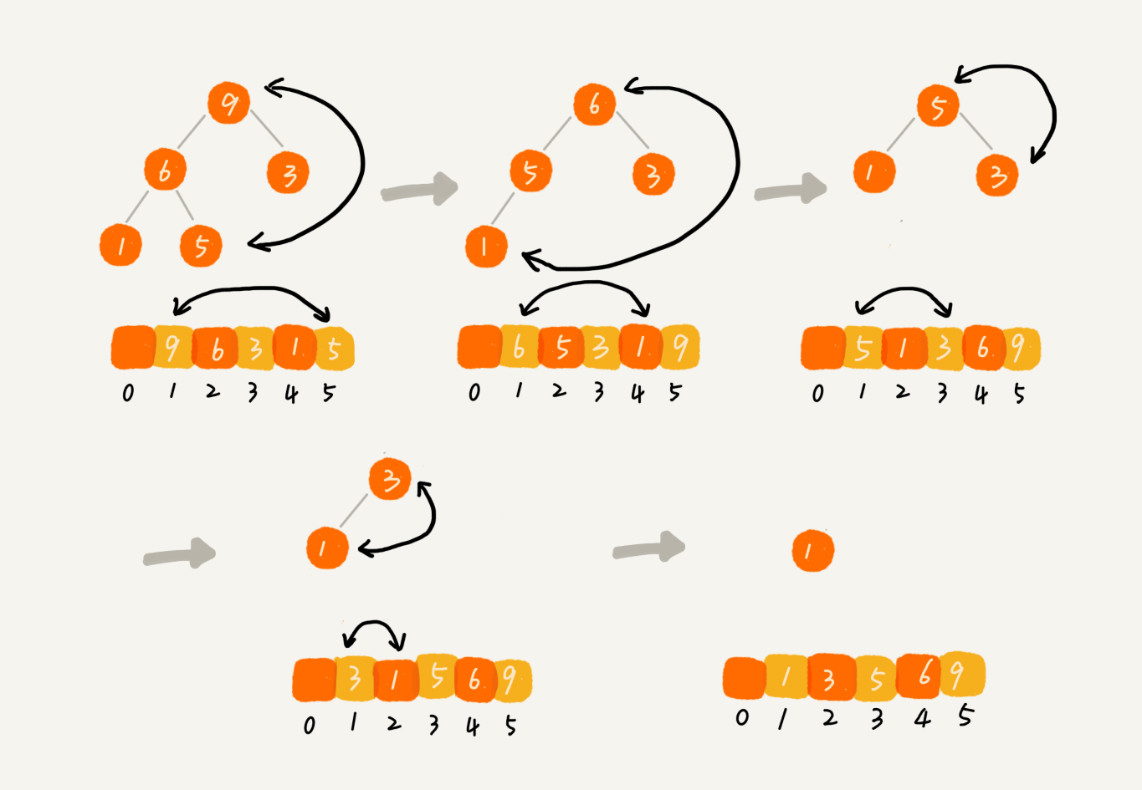
实现代码
1 def sort(self):
2 self.buildheap() # 建堆
3 k = self.count # 获取当前堆中的元素个数
4 while k > 1:
5 self.a[k], self.a[1] = self.a[1], self.a[k] # 交换最后一个和第一个元素的位置
6 k-=1 # 个数减一
7 tem = 1 # 从当前向下堆化
8 while True:
9 index = tem
10 if tem * 2 <= k and self.a[tem] < self.a[tem * 2]: # 在子节点中选取出最大的节点继续宁交换
11 index = tem * 2
12 if tem * 2 + 1 <= k and self.a[index] < self.a[tem * 2 + 1]:
13 index = tem * 2 + 1
14 if index == tem: # 堆化完毕,返回
15 break
16 self.a[tem], self.a[index] = self.a[index], self.a[tem] # 交换值,继续堆化
17 tem = index
因此在堆排序的过程中包含两个部分,建堆过程的时间复杂度为O(n), 排序的过程为O(n log n)。所以整体的时间复杂度为O(nlogn)。堆化和排序都是在数组上直接金聪操作,所以为原地排序。不是稳定排序。
最后总结
为什么堆排序和快排都是O(nlogn)的时间复杂度,但是堆排序应用并不广泛?
第一点,堆排序数据访问的方式没有快速排序友好。因为对于快速排序来说,数据是顺序访问的。而对于堆排序来说,数据是跳着访问的。
第二点,对于同样的数据,在排序过程中,堆排序算法的数据交换次数要多于快速排序。在排序算法中有序度和逆序度的概念。对于基于比较的排序算法来说,整个排序过程就是由两个基本的操作组成的,比较和交换(或移动)。快速排序数据交换的次数不会比逆序度多。但是堆排序的第一步是建堆,建堆的过程会打乱数据原有的相对先后顺序,导致原数据的有序度降低。比如,对于一组已经有序的数据来说,经过建堆之后,数据反而变得更无序了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号