【算法】归并排序
归并排序
对于一个待排序的数组,先将数组分成两部分,如果划分之后的一部分数组数目大于1,则我们继续对其划分,直到分成单个元素的数组。然后我们在申请相应的辅助空间,将两个数组进行进行合并,得到一个排序之后的数组,然后反复进行对比排序,直到生成一个最终和原数组一样大的排好序的数组。
归并排序使用的是分而治之的思想,简单的来说就是将一个大问题,分解成很多小问题,然后从小的问题开始解决,但小的问题解决了,大的问题也就解决了。
复杂度分析
归并排序在排序过程中使用了辅助空间,来依此放置最小的元素,所以其空间复杂度为O(n),时间复杂度为O(nlogn),这里和快排不一样,快排平均时间复杂度为O(nlogn),但是有些时候也会退化成O(n2),存在不稳定的因素,但是归并排序的时间复杂度比较稳定,一直都是O(nlogn), 这是因为它使用了辅助空间来进行排序。另外它也是一个稳定排序,不是原地排序。
图示步骤
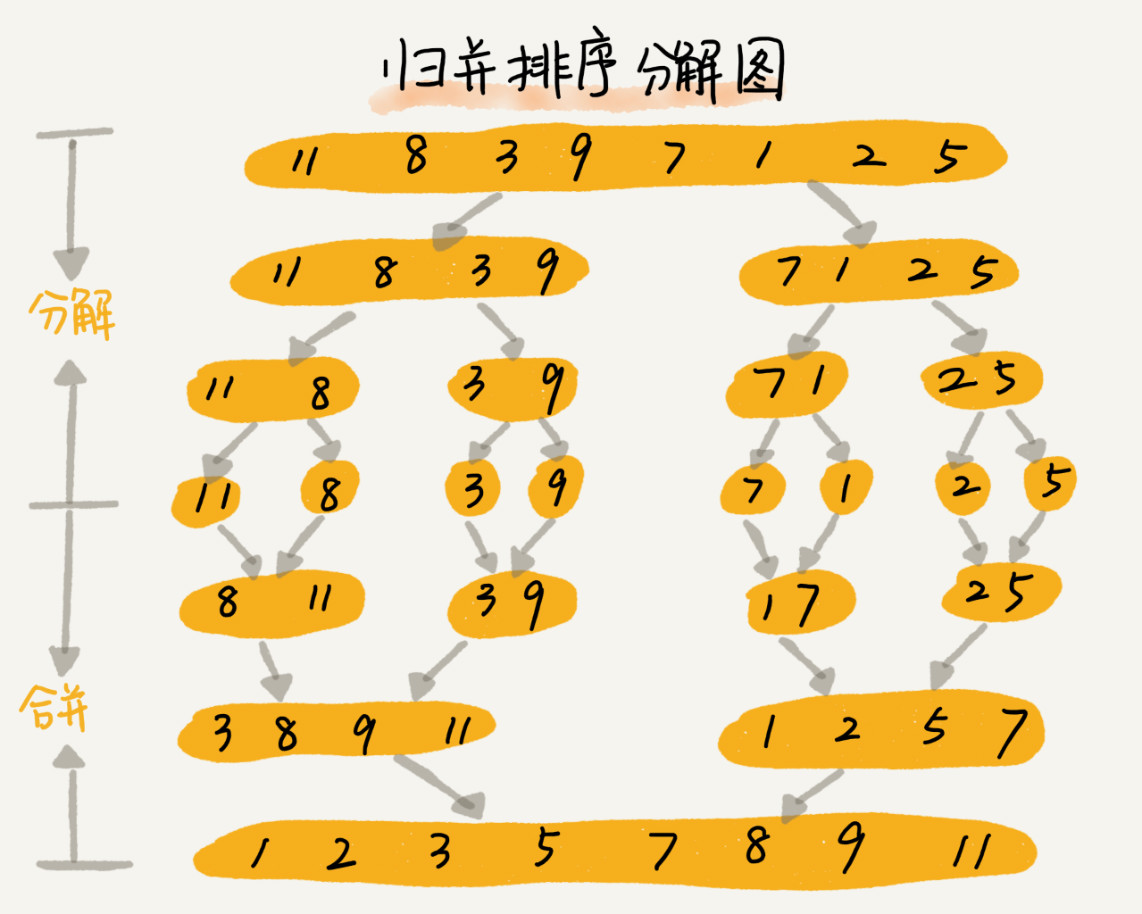
代码实现
1 def merge_sort(arry):
2 if len(arry) < 2:
3 return arry
4 mid = len(arry)//2
5 left = merge_sort(arry[:mid]) # 进行划分
6 right = merge_sort(arry[mid:])
7 return merge(left, right) # 进行合并
8
9
10 def merge(left, right):
11 l_count = r_count = 0
12 tem_arry = [] # 申请辅助数组
13 while l_count < len(left) and r_count < len(right):
14 if left[l_count] < right[r_count]: # 当左边元素小于右边元素时,将左边元素加到辅助数组中
15 tem_arry.append(left[l_count])
16 l_count += 1
17 else:
18 tem_arry.append(right[r_count])
19 r_count += 1
20 if l_count < len(left): # 当一个数组中的元素添加完毕之后,我们检查另外一个数组是否为空,然后将不为空的数组元素添加进去。
21 for i in left[l_count:]:
22 tem_arry.append(i)
23 else:
24 for i in right[r_count:]:
25 tem_arry.append(i)
26 return tem_arry # 返回排好序的数组


