【算法】快排
快速排序
其利用的思想就是分治思想,最开始先从数组中随机选择一个元素p(为什么随机下面解释),然后以这个元素对数组中的元素进行分类,数组左侧都是小于p的元素, 右侧都是大于等于p的元素。这样就让数组分成了两部分。然后我们分别对左边和右边进行进行同样的操作(先随机选择元素,再进行分组)直到所有元素都排完序。
复杂度及优化
时间复杂度为:O(nlogn), 空间复杂度为O(1), 不稳定排序(排序后的数组和排序前的数组中相同元素的位置改变)、原地排序。快排有些时候会出现一些比较大的问题,那就是元素p的选择,如果每次不小心选择了最大的一个元素,那么时间复杂度就会退化为O(n2),这样和选择排序毫无差别,但是我们怎么尽量避免这种情况?那就是改善选择元素的值,一开始我使用的是随机选择法,这种情况下虽然也会存在时间复杂度升高的问题,但是根据概率的情况来说几率不大,随着数组的长度越大,概率也就越低。另外还有一种办法,三数取中法,具体就是我们取第一个元素,中间一个元素和最后一个元素,然后选择大小位于中间的一个元素来作为p,这样也可以大概率避免时间复杂度升高。当数组的长度很大时,我们我们可以适当增加元素个数,比如说取五个元素然后再取大小为中间的值等等。
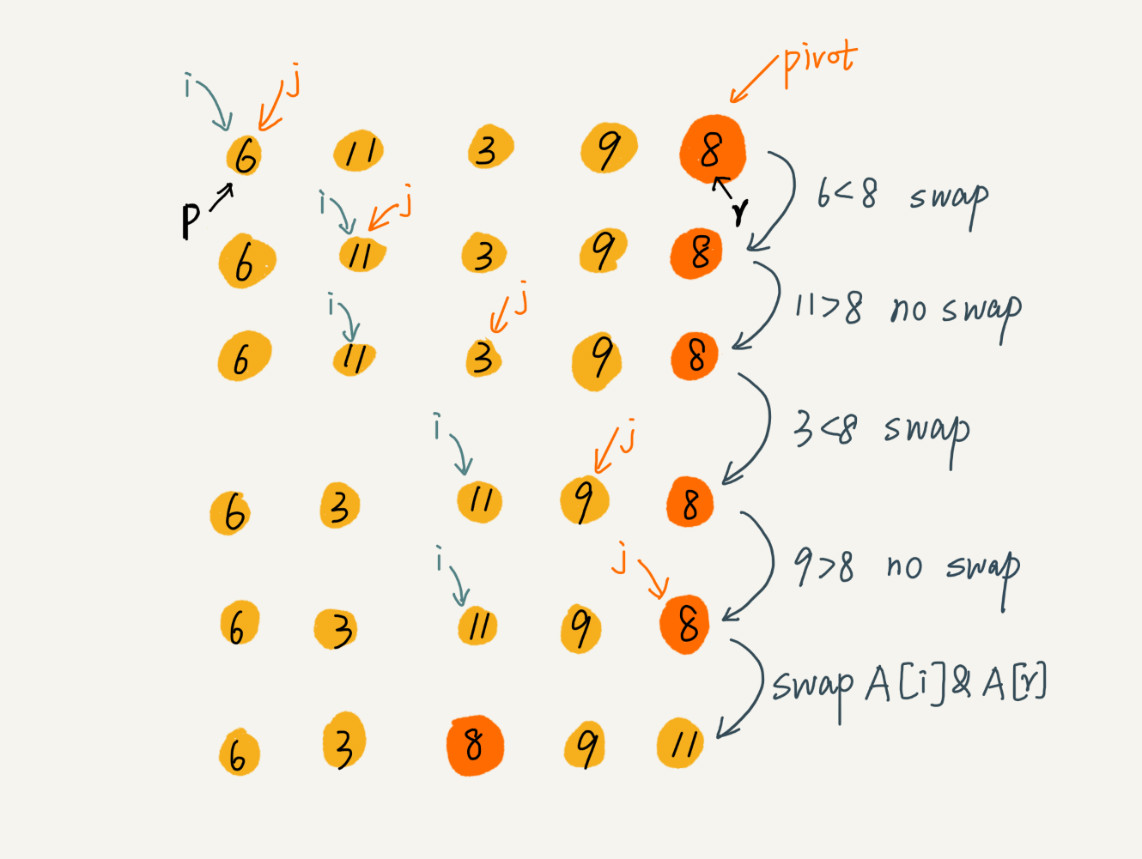
图示步骤
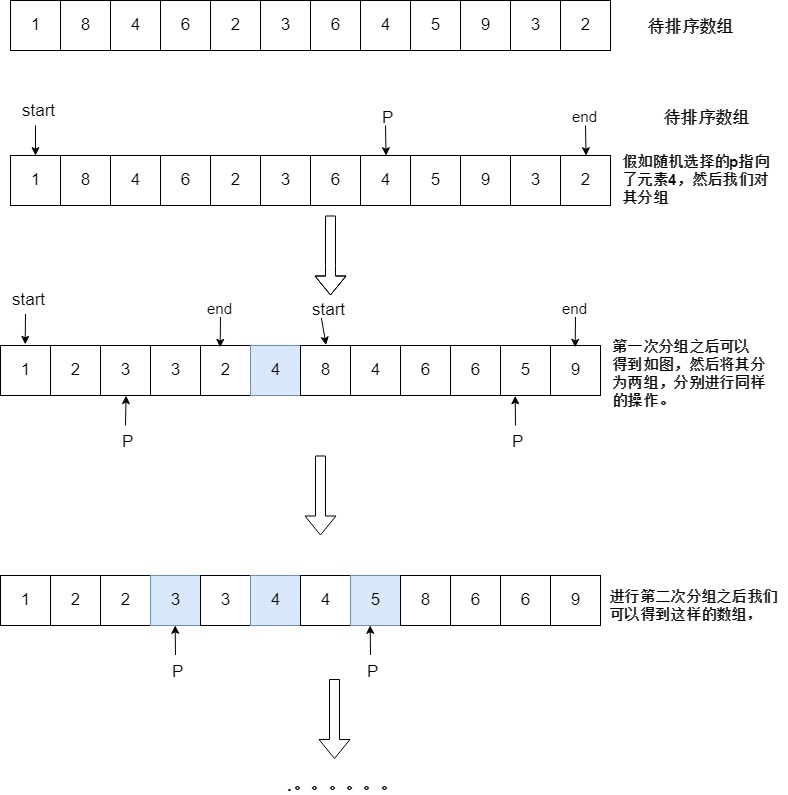
实现代码
1 def quick(arry, start, end):
2 if len(arry) < 2: # 当数组中只有一个元素时就直接返回
3 return
4 index = quickly_sort(arry, start, end) # 第一次进行分组
5
6 if index > start: # 如果分组之后的下标还是大于起始位置,继续进行分组排序。
7 quick(arry, start, index-1)
8 if index < end: # 如果分组之后的下标小于结束位置, 则继续进行分组排序。
9 quick(arry, index+1, end)
10
11
12 def quickly_sort(arry, start, end):
13 if len(arry) < 1:
14 return
15 index = random.randint(start, end) # 随机选择一个下标
16 arry[index], arry[end] = arry[end], arry[index] # 交换下标位置和最后一个元素之间的位置,
17 small = start - 1 # 大于标志元素的标志位
18 for i in range(start, end):
19 if arry[i] < arry[end]:
20 small += 1
21 if small != i:
22 arry[small], arry[i] = arry[i], arry[small] # 交换两个元素
23 small += 1 #
24 arry[small], arry[end] = arry[end], arry[small] # 最后交换分组之后的分界位置,
25 return small
图示: