[Luogu P1450] [HAOI2008]硬币购物 背包DP+容斥

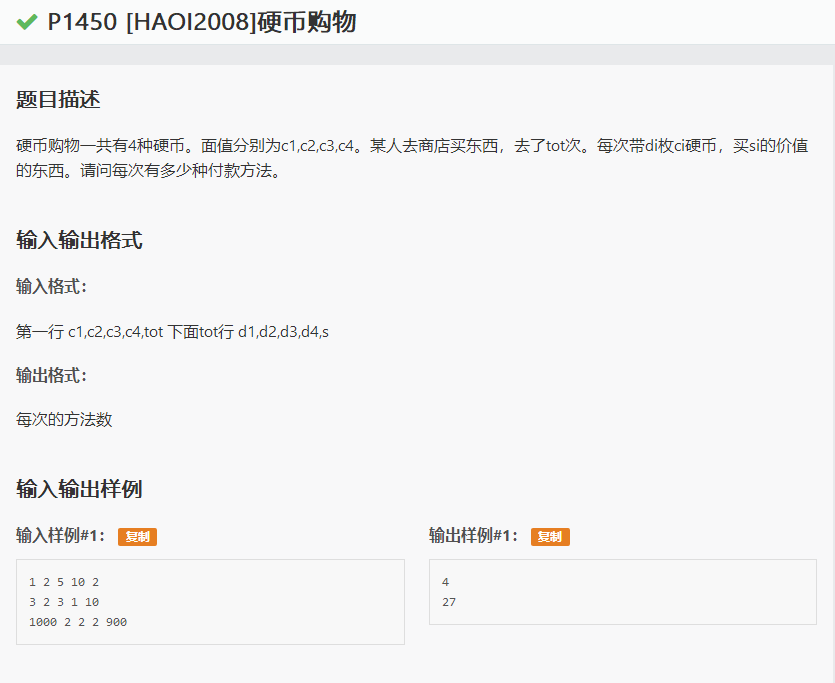
题面

传送门：https://www.luogu.org/problemnew/show/P1450

 

---

 

Solution

这是一道很有意思的在背包里面做容斥的题目。

 

首先，我们可以很轻松地想到暴力做背包的做法。

就是对于每一次询问，我们都做一次背包。

复杂度O(tot*s*log(di)) (使用二进制背包优化)

显然会T得起飞。

 

接下来，我们可以换一种角度来思考这个问题。

首先，我们可以假设没有每个物品的数量的限制，那么这样就会变成一个很简单的完全背包问题。

至于完全背包怎么写，我们在这里就不做过多讨论，如有需要，看看代码就能理解了。

完全背包做完后，我们可以得到一个f[i]表示填满i的背包的方案数的数组。

那么，我们接下来可以用容斥来解决不可行的方案的问题。

 

假设只有1件物品的使用次数超出了所给的数量，假设这件物品是第x件。

那么可以用  f[s-(d[x]+1)*c[x]] 表示这件物品不可行的方案总数。

因为对于花钱数为 s-(d[x]+1)*c[x] 里面的每一种方法，都可以通过使用购买 d[x]+1件的x物品来超出所给的数量。所以  f[s-(d[x]+1)*c[x]] 可以表示该物品不可行方案总数。

 

那么答案是四件物品不可行方案总数这和吗？

nope

因为我们会重复减去一些东西。例如：一种方案即超出了第一件物品的使用数，也超出了第二件物品的使用数，我们却重复扣除了这种方案两次。

所以说我们这时候就得使用容斥来解决这个问题。

容斥中有一个很基础的定理（我不会证）：

对于有n的限制条件的事件，只要其中符合一个条件就算可行，其可行方案总数为：

（符合其中0个（条件的方案数，后同）-符合其中1个+符合其中2个-符合其中3个+符合其中4个-符合其中5个+符合其中6个....）

那么，我们就可以根据这个定理求出不可行的方案总数。

对于这题来说，代码如下:

for(a[1]=0;a[1]<=1;a[1]++)
            for(a[2]=0;a[2]<=1;a[2]++)
                for(a[3]=0;a[3]<=1;a[3]++)
                    for(a[4]=0;a[4]<=1;a[4]++)
                    {
                        int cnt=0,t_s=s;
                        for(int j=1;j<=4;j++)
                            if(a[j]==1) cnt++,t_s-=(d[j]+1)*c[j];
                        if(cnt%2==0) cnt=1;
                        else cnt=-1;
                        
                        if(t_s>=0)
                            ans=ans+cnt*f[t_s];
                    }

这样写绝对不推荐，因为这样写很丑。

 

那么，这题就可以AC啦

 

---

 

Code

//Luogu P1450 [HAOI2008]硬币购物
//Aug,27th,2018
//DP+容斥
#include <iostream>
#include <cstdio>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=100000+1000;
long long f[N];
int n,m;
long long c[5],d[5];
int main(int argc, char **argv)
{
    for(int i=1;i<=4;i++)
        c[i]=read();
    m=read();
    
    f[0]=1;
    for(int j=1;j<=4;j++)
        for(int i=c[j];i<=100000;i++)
            f[i]+=f[i-c[j]];
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=4;j++)
            d[j]=read();
        int s=read(),a[5];
        long long ans=0;
        for(a[1]=0;a[1]<=1;a[1]++)
            for(a[2]=0;a[2]<=1;a[2]++)
                for(a[3]=0;a[3]<=1;a[3]++)
                    for(a[4]=0;a[4]<=1;a[4]++)
                    {
                        int cnt=0,t_s=s;
                        for(int j=1;j<=4;j++)
                            if(a[j]==1) cnt++,t_s-=(d[j]+1)*c[j];
                        if(cnt%2==0) cnt=1;
                        else cnt=-1;
                        
                        if(t_s>=0)
                            ans=ans+cnt*f[t_s];
                    }
        
        printf("%lld\n",ans);
    }
    return 0;
}