[Luogu P2261] [CQOI2007]余数求和 (取模计算)

题面

传送门：https://www.luogu.org/problemnew/show/P2261

 

---

 

 

Solution

这题显然有一个O（n）的直接计算法，60分到手。

 

接下来我们就可以拿出草稿纸推一推式子了

首先，取模运算在这里很不和谐，我们得转换一下。

对于任意取模计算，我们都有：

 所以，我们可以做以下推算

 

 

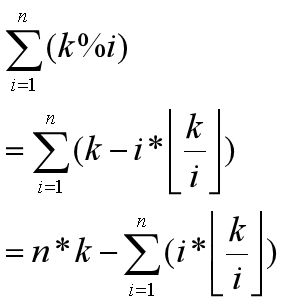
经过一些手算，我们发现k/i(向下取整)是由一段一段的区间组成的，如下图

 

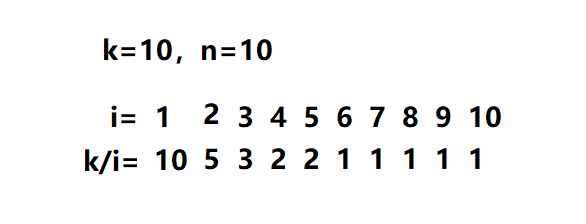
显然，每段区间的右端点可以通过二分的方法来找

对于每一段区间，我们可以把k/i提出来，括号里面就变成了（i+(i+1)+(i+2)+(i+3)+.....+右端点） 直接用等差数列来算就好

 

时间复杂度我不会算XD　　

 

---

 

Code

//Luogu P2261 [CQOI2007]余数求和
//Jul,7th
//取模运算推一推
#include<iostream>
#include<cstdio>
using namespace std;
int main(int argc, char **argv)
{
    //freopen("sum.in","r",stdin);
    //freopen("sum.out","w",stdout);
    long long n,K;
    scanf("%lld%lld",&n,&K);
    
    long long ans=n*K;
    for(long long i=1;i<=n;i++)
    {
        long long temp=K/i;
        long long l=i,r=n,mid,nxt=i;
        while(l<=r)
        {
            mid=(l+r)/2;
            if(K/mid==temp)
                nxt=max(nxt,mid),l=mid+1;
            else
                r=mid-1;
        }
        ans-=(((i+nxt)*(nxt-i+1))/2)*temp;
        i=nxt;
    }
    
    printf("%lld",ans);
    return 0;
}