[Luogu P1613]跑路 (DP+倍增+最短路)

题面

传送门：https://www.luogu.org/problemnew/show/P1613

 

---

 

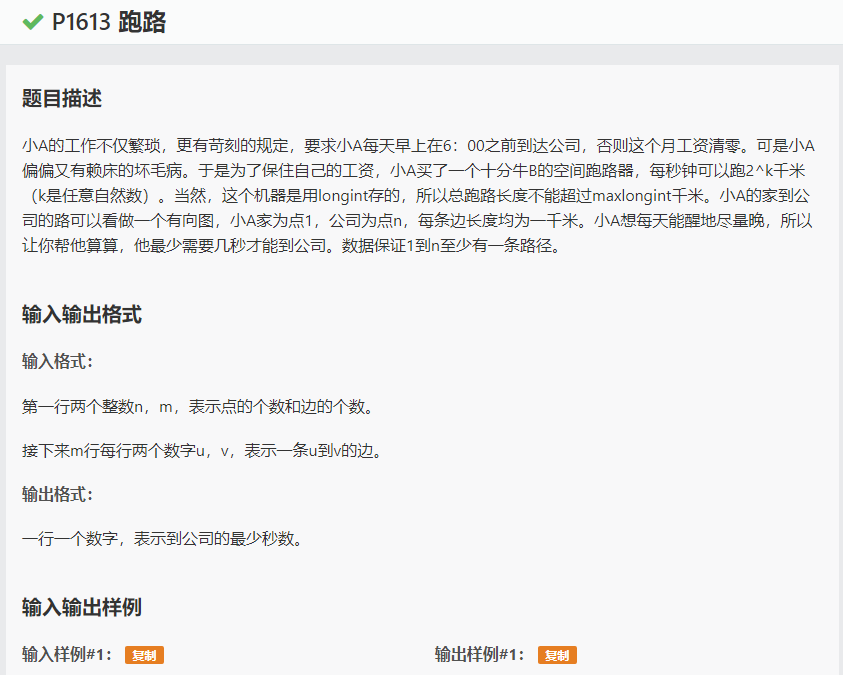
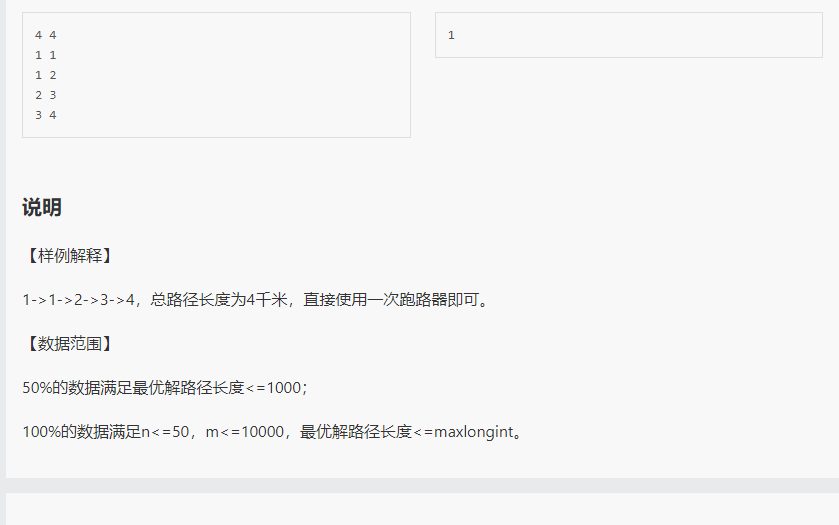
Solution

挺有意思的一道题。

 

题面已经挺明显的描述出了这题的主要思想：倍增。

先这样想，我们可以把这题这样建模：有一堆点，若两个点之间的距离之和可以达到2的n次方，那么这两个点可以用1的时间相互到达。

也就是说，我们把距离能为2的n次方的点对用边权为1的边连上，再做一次最短路径，就可以求出答案了。

 

接下来问题就是如何求出每两个点是否能以2的n次方的时间相互到达。

考虑使用DP。

我们设f[i][j][k] 表示 i到j是否能以2的k次方的距离相互到达。

转移的时候得运用倍增的思想：若两个点能以两端2的k-1次方的距离相互到达，那么两个点就能以2的k次方的距离相互到。

接下来我们就可以运用类似Floyd的办法来处理这个DP，我们可以在最外层枚举这个k，里面三层和Floyd的意义一模一样，就是枚举中转点与起始点。

初始化就是题目中直接相连的两个点，它们的f[a][b][0]=1 （它们距离为1,是2的0次方）

 

时间复杂度： O(n^3*64)

 

---

Code

//Luogu P1613 跑路
//June,13th,2018
//倍增+DP+最短路
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=50+10;
const int K=65+10;
int f[N][N][K],dis[N][N],n,m;
int main()
{
    n=read(),m=read();
    memset(dis,0x3f,sizeof dis);
    for(int i=1;i<=m;i++)
    {
        int s=read(),t=read();
        f[s][t][0]=1;
        dis[s][t]=1;
    }
    
    for(int o=1;o<=64;o++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                for(int k=1;k<=n;k++)
                    if(f[j][i][o-1]==true and f[i][k][o-1]==true)
                    {
                        f[j][k][o]=true;
                        dis[j][k]=1;
                    }
                
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            for(int k=1;k<=n;k++)
                dis[j][k]=min(dis[j][k],dis[j][i]+dis[i][k]);
    
    printf("%d",dis[1][n]);
    return 0;
}