快速傅里叶变换学习笔记(FFT)
什么是FFT
FFT是用来快速计算两个多项式相乘的一种算法。
如果我们暴力计算两个多项式相乘,复杂度必然是\(O(n^2)\)的,而FFT可以将复杂度降至\(O(nlogn)\)
如何FFT
要学习FFT,我们得先了解它的思想。
首先,我们得先了解如何表示一个多项式。显然,我们最传统的方法表示多项式就是表示它的系数就好。但是,如果我们用系数来计算两个多项式相乘,复杂度无论如何都是\(O(n^2)\)的。因此,我们引入点值表示法。
补充资料:什么是点值表示
设A(x)是一个n−1次多项式,那么把n个不同的x代入,会得到n个y。这n对(x,y)唯一确定了该多项式,即只有一个多项式能同时满足“代入这些x,得到的分别是这些y”。
由多项式可以求出其点值表示,而由点值表示也可以求出多项式。
——胡小兔dalao的博客
所以说,我们要表示一个n-1次多项式,可以用n个点值来表示。如果用点值来计算两个多项式相乘,那就很简单了,我们只需要两个多项式的点值两两对应相乘即可(如果两个多项式次数不同,我们也必须让次数较小的那个多项式强行算够一样多的点值(即多取几个\(x\)来计算即可)),这样做的复杂度是\(O(n)的\)。
因此,如果我们能快速地把一个多项式从系数表示变为点值表示,我们就能快速计算两个多项式相乘啦。
这个快速计算的过程。
1.如何取点
我们要把一个多项式从系数形式变为点值形式,肯定躲不开取\(x\)的过程。先辈傅里叶已经为我们解决了这个问题。他取的\(x\)为虚数。
如果您没有学习过复数,请移步胡小兔dalao的博客,他有详细的讲解。
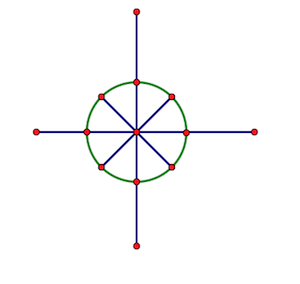
所以说,我们是假设把一个单位圆分成n份(纵坐标为虚部,横坐标为实部),单位圆上我们每取的一个点所代表的虚数(实部与虚部相加)即对应一个\(x\)
根据我们的数学知识,圆上的任意一个我们取出来的点的坐标都可以表示为\((cos((k*2*pi)/n),sin((k*2*pi)/n))\)的形式,逆时针将这\(n\)个点从\(0\)开始编号,第\(k\)个点对应的虚数记作\(ω_n^k\)
补充资料:单位根的性质
性质一:\(ω^{2k}_{2n}=ω^k_n\)
证明:它们对应的点/向量是相同的。
性质二:\(ω^{k+n/2}_n=−ω^k_n\)
证明:它们对应的点是关于原点对称的(对应的向量是等大反向的)。
——胡小兔dalao的博客
这样子,我们就取出了\(n\)个\(x\)
补充资料:为什么要取这些点
如果我们取这些点,我们最后可以快速地把点值式转换为系数式,具体方法及证明见下文
2.如何快速算出每个\(x\)对应的多项式的值
这就涉及到FFT的核心算法了。如果我们暴力去算,复杂度依旧是\(O(n^2)\),并没有什么用。因此,我们FFT的核心思想是分治。
我们先把原多项式拉出来:
\(A(x)=a_0*x^0+a_1*x^1+a_2*x^2+a_3*x^3+a_4*x^4+...+a_{n-1}*x^{n-1}\)
设两个新的多项式:
\(A_1(x)=a_0*x^0+a_2*x^1+a_4*x^2+a_6*x^3+...a_{n-2}*x^{n/2-1}\)
\(A_2(x)=a_1*x^0+a_3*x^1+a_5*x^2+a_7*x^3+...a_{n-1}*x^{n/2-1}\)
显然我们有:
\(A(x)=A_1(x^2)+x*A_2(x^2)\)
所以说,我们可以把原来得式子分成两个长度只有一半的式子,每次都能减少一半的计算量,这样子,我们复杂度就变成了\(O(n*logn)\)
假设我们已经递归下去算出了\(A_1\)与\(A_2\)在\((\omega_{\frac{n}{2}}^{0}, \omega_{\frac{n}{2}}^{1}, \omega_{\frac{n}{2}}^{2}, ... , \omega_{\frac{n}{2}}^{\frac{n}{2} - 1})\)的值,怎么合并回\(A\)在\((\omega_n^{0}, \omega_n^{1}, \omega_n^{2}, ... , \omega_n^{n-1})\)的值呢?
我们把\(\omega_n^x\)带回我们刚刚的这个式子:\(A(x)=A_1(x^2)+x*A_2(x^2)\)有:
\(A(\omega_n^x)=A_1(\omega_n^{x^2})+\omega_n^x*A_2(\omega_n^{x^2})\)
\(A(\omega_n^x)=A_1(\omega_{n/2}^{x})+\omega_n^x*A_2(\omega_{n/2}^{x})\)
那另外那一半怎么算呢?
同样把\(\omega_n^{x+n/2}\)带入\(A(x)=A_1(x^2)+x*A_2(x^2)\)有:
\(A(\omega_n^{k + \frac{n}{2}}) = A_1(\omega_n^{2k + n}) + \omega_n^{k + \frac{n}{2}}A_2(\omega_n^{2k + n})\)
$A(\omega_n^{k + \frac{n}{2}}) = A_1(\omega_{\frac{n}{2}}^{k} \times \omega_n^n) + \omega_n^{k + \frac{n}{2}} $ $A_2(\omega_{\frac{n}{2}}^{k} \times \omega_n^n) \(
\)A(\omega_n^{k + \frac{n}{2}}) = A_1(\omega_{\frac{n}{2}}^{k}) - \omega_nkA_2(\omega_{\frac{n}{2}})$ [1]
实现上,差不多长这样:
const double PI=acos(-1);
typedef complex <double> cp;
inline cp omega (int K,int n)
{
return cp(cos(2*PI*K/n),sin(2*PI*K/n));
}
void FFT(cp a[],int n,bool type)
{
if(n==1) return;
static cp buf[M];
int m=n/2;
for(int i=0;i<m;i++)
buf[i]=a[i*2],buf[i+m]=a[i*2+1];
for(int i=0;i<n;i++)
a[i]=buf[i];
FFT(a,m,type);
FFT(a+m,m,type);
for(int i=0;i<m;i++)
{
cp x=omega(i,n);
if(type==true) x=conj(x);//conj在这里做取倒的作用,具体作用请看下文第四点
buf[i]=a[i]+x*a[i+m];
buf[i+m]=a[i]-x*a[i+m];
}
for(int i=0;i<n;i++)
a[i]=buf[i];
}
3.后续优化
理论上来说,我们已经可以实现FFT了,很不幸的是,递归版本的常数巨大(递归消耗以及大量的三角函数计算),我们可以通过一些玄学方法来优化这份FFT代码:
在进行fft时,我们要把各个系数不断分组并放到两侧,那么一个系数原来的位置和最终的位置有什么规律呢?
初始位置:0 1 2 3 4 5 6 7
第一轮后:0 2 4 6|1 3 5 7
第二轮后:0 4|2 6|1 5|3 7
第三轮后:0|4|2|6|1|5|3|7
“|”代表分组界限。
可以发现(这你都能发现?),一个位置a上的数,最后所在的位置是“a二进制翻转得到的数”,例如6(011)最后到了3(110),1(001)最后到了4(100)。
那么我们可以据此写出非递归版本fft:先把每个数放到最后的位置上,然后不断向上还原,同时求出点值表示。 [1:1]
代码大概长这样:
void FFT(cp a[],int n,bool type)
{
static int len=0,t_num=n-1,t[N];
while(t_num!=0) t_num/=2,len++;
for(int i=0,j;i<=n;i++)
{
for(t_num=i,j=0;j<len;j++)
t[j]=t_num%2,t_num/=2;
reverse(t,t+len);
for(t_num=0,j=0;j<len;j++)
t_num+=t[j]*(1<<j);
if(i<t_num) swap(a[i],a[t_num]);
}
for(int l=2;l<=n;l*=2)
{
int m=l/2;
cp x0=omega(1,l);
if(type==true) x0=conj(x0);
for(int i=0;i<n;i+=l)
{
cp x=cp(1,0);
for(int j=0;j<m;j++,x*=x0)
{
cp temp=x*a[i+j+m];
a[i+j+m]=a[i+j]-temp;
a[i+j]=a[i+j]+temp;
}
}
}
}
4.怎么把点值式换回系数
FFT有一个性质:把多项式\(A(x)\)的离散傅里叶变换结果作为另一个多项式\(B(x)\)的系数,取单位根的倒数即\(ω^0_n,ω_n^{-1},ω_n^{-2},...,ω^{-n+1}_n\)作为\(x\)代入\(B(x)\),得到的每个数再除以\(n\),得到的\(是A(x)\)的各项系数啦。
补充资料:如何证明这个性质
我们设带入后\(B\)的某个点值为\(z_k\),多项式\(B\)算出来的某个点值为\(j_i\),我们有:
$z_k = \sum_{i = 0}^{n - 1} y_i(\omega_n{-k})i \( \)z_k= \sum_{i = 0}^{n - 1}(\sum_{j = 0}^{n - 1} a_j(\omega_ni)j)(\omega_n{-k})i \( \)z_k= \sum_{j = 0}^{n - 1}a_j(\sum_{i = 0}^{n - 1}(\omega_n^{j - k})^i)\( [^1] 这里的\)\sum_{i = 0}^{n - 1}(\omega_n^{j - k})^i\(是可以求出来得,当\)j=k\(的时候,这个式子等于n,其他时候均为0(使用等比数列求和即可证明) 因此我们有:\)z_k=n*a_k$。
证毕
最后的最后......
恭喜你,到此为止,你已经学会了FFT
撒花✿✿ヽ(°▽°)ノ✿
这一段抄自胡小兔dalao的博客 ↩︎ ↩︎


