数据结构专用
0、建模的本质:从问题中抽取关键的对象,找出这些对象之间的关系,以合适的语言或符号加以描述; 问题的种类:数值型,非数值型 ;
逻辑结构:图结构,树结构,线性结构,集合结构 ;物理结构:数据元素及关系在计算机内存中的存储方式
1、将元素“42,30,74,56,15,60”依次插入开始为空的检索树,那么不成功查找的平均查找长度为 3 (21/7),不成功的结点为7,2×2+3×3+2×4=21;
2、具有5层结点的AVL树至少有 12 个结点
3、时间复杂度不受数据初始状态影响而恒为O(nlogn)的是 堆排序
4、高为h的m元树(m≥2, h≥1)中结点总数n<=(mh-1)/(m-1)
5、已知一棵二叉树的先序序列是A,B,C,D,E,F,G,和整数序列3,0,0,6,0,0,0。其中,整数序列中的第i个数,表示先序序列第i个结点的右儿子在先序序列中的序号(序号从1编起,0表示无右儿子)。请问此二叉树中以结点D为根的子树的结点个数为 4
6、就排序算法所用的辅助空间而言,堆排序、快速排序、归并排序的关系是,堆排序<快速排序<归并排序
7、二维数组A的元素都是6个字符组成的串,行下标i的范围从0到8,列下标j的范围从1到10,则A的第8列和第5行共占108个字节,第8列9个元素,第5行10个元素,共9+10-1个元素,18×6==108;
8、设一棵二叉树的结点个数为18,则它的高度至少为 5,2h-1,24-1==15
9、在文件“局部有序”或文件长度较小的情况下,最佳内部排序的方法是,直接插入排序;
10、对关键字序列(56,23,78,92,88,67,19,34)进行增量为3的一趟希尔排序的结果为(19,23,67,56,34,78,92,88);56,92,19;23,88,34;78,67;增量为3的,三组分别排序;一趟后,结果19,23,67,56,34,78,92,88;
11、采用排序算法对n个元素进行排序,其排序趟数肯定为n-1趟的排序方法是,直接选择和插入 ;A 直接插入和快速排序,B 冒泡和快速排序,C 直接选择和堆排序,D 直接选择和插入排序
12、设有5000个待排序的记录关键字,如果需要用最快的方法选出其中最小的10个记录关键字,则用下列( 堆排序 )方法可以达到此目的,A 快速排序,B 直接选择排序,C 归并排序,D 堆排序;
13、在对n个元素进行选择排序的过程中,第i趟需从 n-i+1 个元素中选出最小值元素;第i趟,是从1开始计算的,没有第0趟,第一趟即 n-1+1,从n个元素中选择;
14、对于简单无向图而言,一条回路至少含有3条边;对于无向加权图而言,其最小生成树有可能不存在,但如果存在的话通常是不唯一的;n个顶点的有向图中,顶点的最大度数等于2(n-1);对含有k个连通分量的无向图进行先深搜索时,主控函数中需要调用递归的搜索函数dfs k 次;对于无向图的邻接矩阵,第i行上的非零元素个数和第i列的非零元素个数一定相等;
15、对于n个顶点,m条边的无向图G,若m≥n,则G中必含回路
16、n个顶点的有向图中,顶点的最大度数等于2(n-1),出度n-1,入度n-1
17、在具有n个顶点的图G中,若最小生成树不唯一,则G的边数一定大于n-1;生成树有n个顶点和n-1条边。最小生成树是权值之和最小的那棵生成树。若最小生成树不唯一,一定是有权值相等的边,但未必是权值最小的边相等。最小生成树的代价一定相等。当然,G的边数一定大于n-1,否则,就只有一棵生成树了。
18、在有向图的邻接表存储结构中,顶点v在链表中出现的次数是顶点v的入度;对于有向图,vi的邻接表中每个表结点都对应于以vi为始点射出的一条边。因此,将有向图的邻接表称为出边表。所以顶点V在链表中出现的次数是顶点V的入度
19、一个有向图,共有n条弧,则所有顶点的度的总和为2n
20、如果含有n个顶点的图形成一个环,则它有 n 棵生成树;n个顶点形成的环有n条边,若得到生成树只需要删除这n条边中的任意一条即可,所以得到n棵生成树
21、一个关键活动提前完成,只能让这条关键路径变成非关键路径。当关键路径不止一条的时候,单单提高一条关键路径上关键活动的速度,是不能缩短整个工程工期的。所以,并不是网中任何一个关键活动提前完成,整个工程都能提前完成。但如果网中任何一个关键活动延期完成,整个工程一定延期。
22、连通分量是 无向图 的极大连通子图
23、一个具有n个顶点的有向图中,要连通全部顶点至少需要 n 条弧
24、判断一个有向图是否存在回路,可以用深度优先遍历算法 ,当有向图中无回路时,从某顶点出发进行深度优先遍历时,出栈的顺序(退出DFSTraverse算法)即为逆向的拓扑序列。
25、若一个无向图以顶点V1为起点进行深度优先遍历,所得的遍历序列唯一,则可以唯一确定该图
26、图的路径,由邻接顶点构成的序列
27、带权有向图G用邻域矩阵A存储,则顶点i的入度等于A中,第i列非∞且非零的元素个数
28、对于含有n个顶点的带权连通图,它的最小生成树是指图中任意一个,由n个顶点构成的边的权值之和最小的连通子图
29、无向连通图,所有顶点的度之和为偶数
30、最小生成树的代价唯一
31、具有12个关键字的有序表,折半查找的平均查找长度 37/12,将12个数画成完全二叉树,第一层有1个、第二次2个、第三层4个,第四层只有5个。二分查找时:第一层需要比较1次,第二两个数,每个比较2次,第三层四个数,每个比较3次,第四层五个数,每个比较4次,则平均查找长度即为37/12;
32、如果要求用线性表既能较快地查找,又能适应动态变化的要求,则可采用 分块查找 方法;分块查找是将表分成若干块,分块的原则是数据元素的关键字在块与块之间是有序的,而块内元素的关键字是无序的,其可以适应动态变化的要求;
33、简单选择排序和堆排序性能都受初始序列顺序的影响,是错的
34、在对n个关键字进行直接选择排序的过程中,每一趟都要从无序区选出最小关键字元素,则在进行第i趟排序之前,无序区中关键字元素的个数为 n-i+1
35、将两个各有n个元素的有序表合并成一个有序表,其最少的比较次数为 n
36、在对n个元素进行快速排序的过程中,最坏情况下需要进行 n-1 趟
37、通过先序遍历可以删除二叉树中所有的叶子结点。
38、完全二叉树,可由其先序序列唯一确定,完全二叉树,可由其中序序列唯一确定,满二叉树,可由其后序序列唯一确定
39、含3个结点的普通树的树形共有2种
40、假定一棵三叉树的结点数为50,则它的最小高度为5: 结点数相同而高度最小的三叉树是满三叉树或完全三叉树(深度为h的三叉树,若前面h-1层是满的,只有第h层从右边连续缺若干个结点的三叉树称为完全三叉树)。根据完全二叉树的性质4 (即具有n个结点的完全二叉树,其深度h=[log2n]+1),可推得三叉树的相应性质,即具有n个结点的完全三叉树,其深度h = [log3n]+1。故具有50个结点的三叉树,其最小高度为[log350]+1=5。
41、在哈夫曼树中,若编码长度只允许小于等于4,则除了已确定两个字符的编码为0和10外,还可以最多对 4 个字符进行编码。1100 1101 1110 1111
42、判断:一棵二叉树中,中序遍历序列的最后一个结点,必定是该二叉树前序遍历的最后一个结点。(错,右子树有左子树不一样)
43、具有n片叶子的完全二叉树共有2个
44、给定有n个结点的向量,建立一个有序单链表的时间复杂度 O(n^2)
45、在一个单链表HL中,若要向表头插入一个由指针p指向的结点,则执行p->next = HL; HL = p;
46、将两个各有n个元素的有序表归并成一个有序表,在最坏的情况下,其比较次数是 2n-1
47、对顺序存储的线性表,设其长度为n,在任何位置上插入或删除操作都是等概率的。插入一个元素时平均要移动表中的 n/2 个元素。
48、在一个长度为n的线性表中顺序查找值为x的元素时,查找时的平均查找长度(即x同元素的平均比较次数,假定查找每个元素的概率都相等)为(n+)/2
49、单链表,删除指针指向的结点,通过复制后继结点的数据的方式,实现删除:设指针变量p指向单链表中结点A,若删除单链表中结点A,则需要修改指针的操作序列为:q=p->next;p->data=q->data;p->next=q->next;free(q);
50、m行n列的矩阵,非零项个数为t, t / (m*n) <= 0.3 的矩阵为稀疏矩阵。
51、三种特殊矩阵:上三角,下三角矩阵,带状矩阵(采取顺序存储);稀疏矩阵(采取三元组顺序存储,十字链表链式存储,都不可随机访问)。
52、下三角矩阵存储元素地址计算公式 :loc(i,j) = loc(1,1) + ( i*(i-1)/2 + j -1 )*size (等差数列)
53、上三角矩阵存储元素地址计算公式 :loc(i,j) = loc(1,1) + ( (i-1)*(2*n-i+2)/2 + j -i )*size,(等差数列)n为矩阵列数
54、带状矩阵存储元素地址计算公式:loc(i,j) = loc(1,1) + ( 2+3*(i-2) + j -i+1)*size,
55、十字链表定义(行链表,列链表组成)

//十字链表结点定义 typedef struct OLNode { int row,col; //行,列 ElemType value; struct OLNode *right, *down;//行列指针 }OLNode, *OLink; //十字链表定义 typedef struct { OLink *row_head, *col_head; //行列链表头指针数组 int m, n; //m行,n列 }CrossList;
56、算法原地工作是指算法所需的辅助空间是常量 ,空间复杂度O(1),表示所需空间为常量,并且与n无关
57、数据结构:带结构的数据元素。
58、堆是完全二叉树,是有序的,存储可以用数组连续存储
59、https://blog.csdn.net/shuiyixin/article/category/7555856
60、迭代,逻辑上,多次使用同一算法。
61、排序

#include<stdio.h> #define N 50 #include<stdlib.h> #define INSERT_SROT 0 #define SHELL_SROT 1 #define BUBBLE_SROT 2 #define QUICK_SORT 3 #define SIMPLE_SELECTION_SROT 4 #define HEAP_SORT 5 #define MERGING_SROT 6 #define MOVING_COUNT 0 #define COMPARING_COUNT 1 int result[7][2]; void InsertionSort(int * pData, int n) { int temp; for (int i = 1; i < n; i++) { temp = pData[i]; for (int j = i - 1; j >= 0 && temp < pData[j]; j--) { pData[j+1]= pData[j]; result[INSERT_SROT][MOVING_COUNT]++; result[INSERT_SROT][COMPARING_COUNT]++; } pData[i+ 1] = temp; result[INSERT_SROT][MOVING_COUNT]++; } } void ShellSort(int * pData, int n, int delta) { int temp; for (int i = 1; i < n; i = i + delta) { temp = pData[i]; for (int j = i - delta; j >= 0 && temp < pData[j]; j = j - delta) { result[SHELL_SROT][MOVING_COUNT]++; result[SHELL_SROT][COMPARING_COUNT]++; pData[j + delta] = pData[j]; } pData[i + delta] = temp; result[SHELL_SROT][MOVING_COUNT]++; } } void Shell(int * pData, int n) { int k = 4; while(k>=1) { ShellSort(pData, n, k); k = k / 2; } } void BubbleSort(int a[], int n) { int temp; for (int i = 1; i <= n - 1; i++) { for (int j = 1; j <= n - i; j++) { result[BUBBLE_SROT][COMPARING_COUNT]++; if (a[j - 1] > a[j]) { temp = a[j]; a[j] = a[j - 1]; a[j - 1] = temp; } result[BUBBLE_SROT][MOVING_COUNT] += 3; } } } int Parition(int a[], int i, int j) { int temp = a[j]; while (i < j) { while (a[j] >= temp && i < j) { j--; result[QUICK_SORT][COMPARING_COUNT]++; } if (i < j) { a[i++] = a[j]; result[QUICK_SORT][MOVING_COUNT]++; } while (a[i] <= temp && i < j) { i++; result[QUICK_SORT][COMPARING_COUNT]++; } while (a[i] <= temp && i < j) { i++; result[QUICK_SORT][COMPARING_COUNT]++; } if (i < j) { a[j--] = a[i]; result[QUICK_SORT][MOVING_COUNT]++; } } a[i] = temp; result[QUICK_SORT][MOVING_COUNT]++; return i; } void QuickSort(int a[], int i, int j) { int k; if (i < j) { k = Parition(a, i, j); QuickSort(a, i, k - 1); QuickSort(a, k + 1, j); } } void SimpleSelectionSort(int a[], int n) { int min; int temp; for (int i = 0; i < n - 1; i++) { min = i; for (int j = i + 1; j < n; j++) if (a[j] < a[min]) { min = j; result[SIMPLE_SELECTION_SROT][COMPARING_COUNT]++; } temp = a[i]; a[i] = a[min]; a[min] = temp; result[SIMPLE_SELECTION_SROT][MOVING_COUNT] += 3; } } #define LeftChild(i)(2*(i)+1) void BuildDown(int a[], int n, int rootIndex) { int root = a[rootIndex]; int childIndex = LeftChild(rootIndex); while (childIndex < n) { childIndex++; result[HEAP_SORT][COMPARING_COUNT]++; if (root < a[childIndex]) { a[rootIndex] = a[childIndex]; result[HEAP_SORT][COMPARING_COUNT]++; rootIndex = childIndex; childIndex = LeftChild(rootIndex); } else break; } a[rootIndex] = root; } void HeapSort(int a[], int n) { int temp; for (int rootIndex = (n - 2) / 2; rootIndex >= 0; rootIndex--) BuildDown(a, n, rootIndex); for (int i = n - 1; i >= 0; i--) { temp = a[0]; a[0] = a[i]; a[i] = temp; result[HEAP_SORT][COMPARING_COUNT] += 3; BuildDown(a, i, 0); } } void Merge(int a[],int s1,int e1,int s2,int e2,int b[]) { int k = s1; int i = s1; while ((s1 <= e1) && (s2 <= e2)) { result[MERGING_SROT][COMPARING_COUNT]++; if (a[s1] <= a[s2]) { b[k++] = a[s1++]; result[MERGING_SROT][MOVING_COUNT]++; } else { b[k++] = a[s2++]; result[MERGING_SROT][MOVING_COUNT]++; } } while (s1<=e1) { b[k++] = a[s1++]; result[MERGING_SROT][MOVING_COUNT]++; } while (s2 <= e2) { b[k++] = a[s2++]; result[MERGING_SROT][MOVING_COUNT]++; } k --; while (k>= i) { a[k] = b[k]; k--; result[MERGING_SROT][MOVING_COUNT]++; } } void MergeSort(int a[], int i, int j, int b[]) { int k; if (i < j) { k = (i + j) / 2; MergeSort(a, i, k, b); MergeSort(a, k + 1, j, b); Merge(a, i, k, k + 1, j, b); } } void Generate_Random(int a[], int length, int max, int min) { for (int i = 0; i < length; i++) { a[i] = rand() % (max - min + 1); a[i] += min; } } int data[N], back[N]; int main() { int i, j; for (i = 0; i < 7; i++) for (j = 0; j < 2; j++) result[i][j] = 0; printf("\t\t比较次数\t移动次数\t比较次数(有序)\t移动次数(有序)\n"); Generate_Random(data, 50, 10, 1); InsertionSort(data, 50); Generate_Random(data, 50, 10, 1); Shell(data, 50); Generate_Random(data, 50, 10, 1); BubbleSort(data, 50); Generate_Random(data, 50, 10, 1); QuickSort(data, 0, 49); Generate_Random(data, 50, 10, 1); SimpleSelectionSort(data, 50); Generate_Random(data, 50, 10, 1); HeapSort(data, 50); Generate_Random(data, 50, 10, 1); MergeSort(data, 0, 49, back); int result_back[7][2]; for (i = 0; i < 7; i++) for (j = 0; j < 2; j++) { result_back[i][j] = result[i][j]; result[i][j] = 0; } InsertionSort(data, 50); Shell(data, 50); BubbleSort(data, 50); QuickSort(data, 0, 49); SimpleSelectionSort(data, 50); HeapSort(data, 50); MergeSort(data, 0, 49, back); const char*name[7] = { "插入排序","希尔排序","冒泡排序","快速排序","简单排序","堆排序","归并排序" }; for (i = 0; i < 7; i++) { printf("%-10s", name[i]); for (j = 0; j < 2; j++) printf("\t%d\t", result_back[i][j]); for (j = 0; j < 2; j++) printf("\t%d\t", result[i][j]); printf("\n"); } return 0; }
62、二叉排序树

#include<stdio.h> #include<stdlib.h> #include<time.h> int ASL[4] = {0}; //Average Search Length 查找成功时的平均查找长度 #define SEQ_SEARCH 0 //顺序查找 下标 #define BINARY_SEARCH 1 //二分查找 下标 #define BST_SEARCH 2 //二分查找树 下标 #define BALANCE_SEARCH 3 //平衡查找树 下标 typedef struct Node //定义树结点 { int key; struct Node *pLeft; struct Node *pRight; int bf; //Balance Factor 平衡因子 } Node; //1、SeqSearch 顺序查找 int SeqSearch(int a[], int length, int key) { for (int i = 0; i < length; i++) { ASL[SEQ_SEARCH]++; if (a[i] == key) return i; } return -1; } //2、Binary_Search 二分查找 int Binary_Search(int a[], int n, int key) { int l = 0; int h = n - 1; int m; while (l <= h) { m = (l + h) / 2; ASL[BINARY_SEARCH]++; if (key == a[m])return m; ASL[BINARY_SEARCH]++; if (key < a[m]) h = m - 1; else l = m + 1; } return-1; } //3、SearchBST 二分查找树 ( 查找并插入 ) int SearchBST(Node *pRoot, int key, Node ** pKeyNode, Node ** pParentNode) { *pKeyNode = pRoot; *pParentNode = NULL; while (*pKeyNode) { if (key > (*pKeyNode)->key) { ASL[BST_SEARCH]++; *pParentNode = *pKeyNode; *pKeyNode = (*pKeyNode)->pRight; } else if (key <(*pKeyNode)->key) { ASL[BST_SEARCH]++; *pParentNode = *pKeyNode; *pKeyNode = (*pKeyNode)->pLeft; } else { return 1; } } return 0; } //*3、 SearchBST 二分查找树 ( 纯查找 ) int SearchBST(Node*pRoot, int key) { int found = 0; Node *pKeyNode = pRoot; while (pKeyNode) { if (key > pKeyNode->key) { ASL[BST_SEARCH]++; pKeyNode = pKeyNode->pRight; } else if (key < pKeyNode->key) { ASL[BST_SEARCH]++; pKeyNode = pKeyNode->pLeft; } else { return 1; } } return 0; } //4、SearchBalanceBST 平衡查找树 int SearchBalanceBST(Node*pRoot,int key) { int found = 0; Node *pKeyNode = pRoot; while (pKeyNode) { if (key > pKeyNode->key) { ASL[BALANCE_SEARCH]++; pKeyNode = pKeyNode->pRight; } else if (key < pKeyNode->key) { ASL[BALANCE_SEARCH]++; pKeyNode = pKeyNode->pLeft; } else { return 1; } } return 0; } //二分查找树插入结点 int InsertBST(Node ** pRoot, int key) { Node * pKeyNode = NULL; Node * pParentNode = NULL; if (SearchBST(*pRoot, key, &pKeyNode, &pParentNode)) return 0; Node *pNewNode = (Node*)malloc(sizeof(Node)); pNewNode->key = key; pNewNode->pLeft = pNewNode->pRight = NULL; if (*pRoot == NULL)(*pRoot) = pNewNode; else if (key < pParentNode->key) pParentNode->pLeft = pNewNode; else pParentNode->pRight = pNewNode; return 1; } //二分平衡树旋转操作 void RightRotate(Node ** pNode) { Node * pAxis = (*pNode)->pLeft; (*pNode)->pLeft = pAxis->pRight; pAxis->pRight = *pNode; *pNode = pAxis; } void LeftRotate(Node ** pNode) { Node * pAxis = (*pNode)->pRight; (*pNode)->pRight = pAxis->pLeft; pAxis->pLeft= *pNode; *pNode = pAxis; } void LL_LR_Balance(Node ** pNode) { Node * pLeft = (*pNode)->pLeft; switch (pLeft->bf) { case 1: //RightRotate (*pNode)->bf = pLeft->bf = 0; RightRotate(pNode); break; case -1: //LeftRotate / RightRotate Node*pRight = pLeft->pRight; switch (pRight->bf) { case 0: (*pNode)->bf = pLeft->bf = 0; break; case 1: pRight->bf= pLeft->bf = 0; (*pNode)->bf = -1; case -1: (*pNode)->bf = pRight->bf = 0; pLeft->bf = 1; break; } LeftRotate(&(*pNode)->pLeft); RightRotate(pNode); break; } } void RR_RL_Balance(Node ** pNode) { Node *pRight = (*pNode)->pRight; switch (pRight->bf) { case -1: //LeftRotate (*pNode)->bf = pRight->bf = 0; LeftRotate(pNode); break; case 1: //RightRotate/LeftRotate Node*pLeft = pRight->pLeft; switch (pLeft->bf) { case 0: (*pNode)->bf = pRight->bf = 0; break; case 1: (*pNode)->bf = pLeft->bf = 0; pRight->bf = -1; break; case -1: pRight->bf = pLeft->bf = 0; (*pNode)->bf = 1; break; } RightRotate(&(*pNode)->pRight); LeftRotate(pNode); break; } } //二分平衡树插入 int InsertBalanceBST(Node ** pRoot, int key, int * chain) { if ((*pRoot) == NULL) //找到位置插入 { *pRoot=(Node*)malloc(sizeof(Node)); (*pRoot)->bf = 0; (*pRoot)->pLeft = (*pRoot)->pRight = NULL; (*pRoot)->key = key; *chain = 1; } else //查找插入位置 { if (key == (*pRoot)->key) { *chain = 0; return 0; } if (key < (*pRoot)->key) //LL_LR_Balance { if (!InsertBalanceBST(&(*pRoot)->pLeft, key, chain))return 0; if (*chain) { switch ((*pRoot)->bf) { case 0: (*pRoot)->bf = 1; *chain = 1; break; case 1: LL_LR_Balance(pRoot); *chain = 0; break; case -1: (*pRoot)->bf = 0; *chain = false; break; } } } else //RR_RL_Balance { if (!InsertBalanceBST(&(*pRoot)->pRight, key, chain)) return 0; if (*chain) { switch ((*pRoot)->bf) { case 0: (*pRoot)->bf = -1; *chain = true; break; case 1: (*pRoot)->bf = 0; *chain = false; break; case -1: RR_RL_Balance(pRoot); *chain = false; break; } } } } return 1; } //随机值函数 void Generate_Random(int a[], int length, int max, int min) { for (int i = 0; i < length; i++) { a[i] = rand() % (max - min + 1); a[i] += min; } } //中序打印树 void InorderTraversal( Node* BT ) { if(BT) { InorderTraversal(BT->pLeft); printf(" %d",BT->key); InorderTraversal(BT->pRight); } } //打印数组 void PrintArrayData(int data[]){ int i; for(i=0; i<50; i++) { printf(" %d", data[i]); } printf("\n"); } int main( ) { int data[50]; int back[2]; int temp; int i; //------------------------------------------ for (i = 0; i < 50; i++) //有序数据 data[i] = i; for (i = 0; i < 5000; i++) { Generate_Random(back, 2, 49, 1); temp = data[back[0]]; data[back[0]] = data[back[1]]; data[back[1]] = temp; } //PrintArrayData(data); //数据已经打乱 Node * pTree = NULL; Node * pBTree = NULL; int chain = 0; for (i = 0; i < 50; i++) //插入打乱的数据到二叉树 { InsertBST(&pTree, data[i]); //二叉树 InsertBalanceBST(&pBTree, data[i], &chain); //平衡二叉树 } /* InorderTraversal(pTree); printf("\n"); InorderTraversal(pBTree); printf("\n"); */ //--------------------------------------------- for (i = 0; i < 50; i++) //因为二分查找必须有序 data[i] = i; for (i = 0; i < 4; i++) ASL[i] = 0; for (i = 49; i >= 0; i--) { SeqSearch(data, 50, data[i]); Binary_Search(data, 50, data[i]); SearchBST(pTree, data[i]); SearchBalanceBST(pBTree, data[i]); } const char *name1[] = { "顺序查找","二分查找","二分查找树","平衡查找树" }; for (i = 0; i < 4; i++) { printf("\t%s \t%f\n", name1[i], (float)ASL[i] / 50.0); } return 0; }
63、散列表冲突处理方法:开放地址法(线性探测,平方探测,双散列),分离链接法。线性探测容易产生聚集,平方探测容易探查不到整个散列表空间,但是如果散列表长度TableSize是某个4k+3(k是正整数)形式的素数时,平方探测法就可以探查到整个散列表空间
在开放地址散列表中,当删除散列表中元素时,要将元素标记为deleted,不然在查找时遇到这个空闲位置,会判定为散列表中不存在这个数据(遇到空闲位置不再找了)。在开放地址散列表中,删除操作只能是懒惰删除,即需要增加一个删除标记,而不是真正的删除它,以便查找时不会断链,其空间可以在下次插入时重用
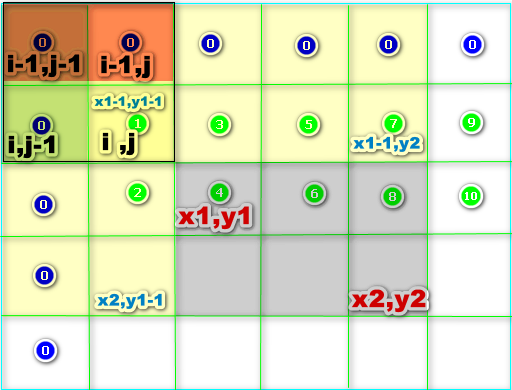
64、子矩阵,二维数组的前缀

#include <stdio.h> int arr[101][101]; int sum[101][101]; int main() { int i,j; //填写数据 arr[1][1]=1; for(i=1,j=2; j<=100; ++j) //第一行 比左边大2 arr[i][j] = arr[i][j-1] + 2; for(i=2;i<=100;i++) //第二行开始 比上面大1 { for(j=1;j<=100;j++) { arr[i][j] = arr[i-1][j] + 1; } } //计算sum数组 ,二维数组的前缀 for( i=1; i<=100; ++i){ //行 for( j=1; j<=100; ++j){//列 sum[i][j] = arr[i][j] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1]; } } int x1,y1,x2,y2; //左上坐标,右下坐标,构成的子矩阵 for(x1=1; x1<=100; ++x1) { for( y1=1; y1<=100; ++y1) { for(x2=x1+1; x2<=100; ++x2){ for(y2 = y1+1; y2<=100; ++y2){ int ret = sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]; if(ret>2022) break; if(ret==2022){ printf("%d,%d,%d,%d\n",x1,y1,x2,y2); goto end; } } } } } end: for(i=x1; i<=x2; ++i){ for(j=y1; j<=y2;++j){ printf("%d,",arr[i][j]); } printf("\n"); } printf( "%d\n", (x2-x1+1 ) * (y2-y1+1 ) ); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号