图的概念、存储、遍历、最短路径问题、最小生成树、拓扑排序、关键路径

Posted on 2019-08-18 16:51 金色的省略号阅读(687) 评论(0) 编辑收藏举报

一、图，顶点（结点）之间的关系是任意的，任何结点之间都可能相关。

　　1、图是由两个集合，顶点集和边集组成的，记作，G = G(V, E)，顶点是数据元素，边是两个顶点之间的关系。

　　2、图分为，有向图、无向图。设顶点(vertex)的个数为n，有n(n-1)/2 条边(edge)的无向图，称为无向完全图；有n(n-1) 条弧的有向图，称为有向完全图。设G = (V,E)是一个图，若V'是V的子集，E'是E的子集，则，G' = (V',E')也是一个图，并称其为G的子图，即一个图的顶点集、边（弧）集属于另一个图的顶点集、边集，这个图就是子图。

　　度， 无向图中顶点v的度是关联与该顶点的边的数目，记作D(v)；有向图中顶点v的度为该顶点的入度和出度之和；
　　入度，有向图中以顶点v为终点的边的数目称为v的入度，记作 ID(v)，出度，有向图中以顶点v为始点的边的数目称为v的出度，记作OD(v)；　　

　　3、与图的边或弧相关的数值叫做权，带权的图叫做网。

　　4、图的路径，在图G = G(V, E) 中，一个顶点x经过一些顶点到达顶点y，称为顶点x到顶点y的路径(邻接顶点构成的序列)，非带权图的路径长度为路径上边的条数，带权的图的路径的长度为路径上各边的权之和。简单路径，序列中顶点不重复的路径称为简单路径。回路，第一个顶点和最后一个顶点相同的路径，叫回路；简单回路，除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的路径称为简单回路。

　　5、连通，在无向图中，如果从顶点x到顶点y存在路径，称x，y是连通的；连通图，无向图G中，如果任意两个顶点之间都是连通的，称图G为连通图；连通分量，无向图中，极大连通子图（极大连通顶点数，再加一个顶点，就不连通了；极大边数，包含子图中所有顶点相连的所有边），称为连通分量。

　　强连通图，有向图中，任意两个顶点之间都是相互可达的，称为图G是强连通图；有向图G的极大强连通子图称为G的强连通分量。

　　6、树图：极小连通子图，在n个顶点的情况下，有n-1条边。

　　7、图的顶点、边、度之间的关系，所有的顶点的度之和除以二，就是边的个数；设图G有n个结点，m条边，且G中每个结点的度数不是k，就是k+1，则G中度数为k的结点数是多少？

　　设度为k的结点数为x，则 ( (n-x)*(k+1) + x*k )/2 == m ， x == n*(k+1) - 2*m

二、图的存储，图需要存储的信息：顶点和边。

　　1、邻接矩阵，表示顶点之间相邻关系的矩阵。无向图的邻接矩阵一定是一个对称矩阵，矩阵的对角元设为0。无向图的邻接矩阵的第i行（或第i列）的非零元素的个数，是第i个顶点的度。有向图的邻接矩阵的第i行的非零元素的个数，是第i个顶点的出度，第j列的非零元素的个数，是第j个顶点的入度。

　　顶点，边，静态数组，插入

 1 /* 图的邻接矩阵表示法 */
 2  
 3 #define MaxVertexNum 100    /* 最大顶点数设为100 */
 4 #define INFINITY 65535        /* ∞设为双字节无符号整数的最大值65535*/
 5 typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
 6 typedef int WeightType;        /* 边的权值设为整型 */
 7 typedef char DataType;        /* 顶点存储的数据类型设为字符型 */
 8  
 9 /* 边的定义 */
10 typedef struct ENode *PtrToENode;
11 struct ENode{
12     Vertex V1, V2;      /* 有向边<V1, V2> */
13     WeightType Weight;  /* 权重 */
14 };
15 typedef PtrToENode Edge;
16         
17 /* 图结点的定义 */
18 typedef struct GNode *PtrToGNode;
19 struct GNode{
20     int Nv;  /* 顶点数 */
21     int Ne;  /* 边数   */
22     WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
23     DataType Data[MaxVertexNum];      /* 存顶点的数据 */
24     /* 注意：很多情况下，顶点无数据，此时Data[]可以不用出现 */
25 };
26 typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
27  
28  
29  
30 MGraph CreateGraph( int VertexNum )
31 { /* 初始化一个有VertexNum个顶点但没有边的图 */
32     Vertex V, W;
33     MGraph Graph;
34      
35     Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
36     Graph->Nv = VertexNum;
37     Graph->Ne = 0;
38     /* 初始化邻接矩阵 */
39     /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
40     for (V=0; V<Graph->Nv; V++)
41         for (W=0; W<Graph->Nv; W++)  
42             Graph->G[V][W] = INFINITY;
43              
44     return Graph; 
45 }
46         
47 void InsertEdge( MGraph Graph, Edge E )
48 {
49      /* 插入边 <V1, V2> */
50      Graph->G[E->V1][E->V2] = E->Weight;    
51      /* 若是无向图，还要插入边<V2, V1> */
52      Graph->G[E->V2][E->V1] = E->Weight;
53 }
54  
55 MGraph BuildGraph()
56 {
57     MGraph Graph;
58     Edge E;
59     Vertex V;
60     int Nv, i;
61      
62     scanf("%d", &Nv);   /* 读入顶点个数 */
63     Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
64      
65     scanf("%d", &(Graph->Ne));   /* 读入边数 */
66     if ( Graph->Ne != 0 ) { /* 如果有边 */ 
67         E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */ 
68         /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
69         for (i=0; i<Graph->Ne; i++) {
70             scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
71             /* 注意：如果权重不是整型，Weight的读入格式要改 */
72             InsertEdge( Graph, E );
73         }
74     } 
75  
76     /* 如果顶点有数据的话，读入数据 */
77     for (V=0; V<Graph->Nv; V++) 
78         scanf(" %c", &(Graph->Data[V]));
79  
80     return Graph;
81 }

图的邻接矩阵表示法

　　邻接矩阵存储图

/*    图的邻接矩阵
借助邻接矩阵很容易判定任意两个顶点之间
是否有边（弧）相连，并容易求得各个顶点的度*/

#include <stdio.h>
#define MAXLEN 10

typedef struct
{
    char vexs[MAXLEN];//顶点向量，存储一串顶点标识
    int edges[MAXLEN][MAXLEN];//表示两个顶点之间的关系
    int n, e;
} MGraph;

//建立一个图的邻接矩阵存储的算法如下：
void CreateMGraph(MGraph &G)
{
    int i, j, k;
    char ch1, ch2;
    printf("请输入顶点数和边数:\n");
    scanf("%d%d", &(G.n), &(G.e));
    printf("请输入顶点标识（构造顶点向量）:\n");
    for(i = 0; i < G.n; i++)
    {
        getchar();
        scanf("%c", &(G.vexs[i]));
    }
    
    /*格式化，任意两顶点之间的关系置为0（fause）*/
    for(i = 0; i < G.n; i++)
        for(j = 0; j < G.n; j++)
            G.edges[i][j] = 0;
    printf("初始化每条边的首尾:\n");
    for(k = 0; k < G.e; k++)
    {
        getchar();
        printf("请输入第%d条边的首尾顶点序号：\n", k + 1);
        scanf("%c%c", &ch1, &ch2);//注意输入时不要加空格
        for(i = 0; ch1 != G.vexs[i]; i++);  //找顶点ch1
        for(j = 0; ch2 != G.vexs[j]; j++);  //找顶点ch2
        //G.edges[i][j]=G.edges[j][i] = 1;//无向图
        G.edges[i][j] = 1;  //有向图 顶点ch1到顶点ch2
    }
}

int main()
{
    MGraph  M;
    CreateMGraph(M);
    int i, j;
    for(i=0; i<M.n; i++)
    {
        for(j=0; j<M.n; j++)
        {
            printf("%d ", M.edges[i][j]);
        }
        printf("\n");
    }
    return 0;
}

View Code

　　头文件，源文件，动态分配二维数组，有向图

 1 /* 
 2     图的邻接矩阵表示及辅助函数 
 3     graphmatrixutil.h
 4 */
 5 
 6 #include <limits.h>
 7 #include <stdio.h>
 8 #include <stdlib.h>
 9 
10 #ifndef GRAPHMATRIXUTIL_H_
11 #define GRAPHMATRIXUTIL_H_
12 
13 /* 图结构体 */
14 typedef struct GRAPHMATRIX_STRU{
15     int size;     /* 图中结点的个数 */
16     int **graph;   /* 二维数组指针 */
17 }GraphMatrix;     /* 定义结构体类型 */
18 
19 /* 初始化图 */
20 GraphMatrix* InitGraph(int num);
21 
22 /* 将数据读入图 */
23 void ReadGraph(GraphMatrix* graphMatrix);
24 
25 /* 将图的结构显示出来 */
26 void WriteGraph(GraphMatrix* graphMatrix);
27 
28 #endif

头文件，graphmatrixutil.h

 1 #include "graphmatrixutil.h"
 2 
 3 /* 初始化图，num表示图中结点个数，邻接矩阵表示图 */
 4 GraphMatrix* InitGraph(int num)
 5 {
 6     int i,j;
 7     /* 图空间定义 */
 8     GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix));    
 9     graphMatrix->size = num;/* 图中结点数 */
10     
11     /* 指针数组分配空间 */
12     graphMatrix->graph = (int**)malloc(sizeof(int*)*graphMatrix->size);
13     /* 指针数组中的指针分配空间 */
14     for(i=0; i<graphMatrix->size; ++i){
15         graphMatrix->graph[i] = (int*)malloc(sizeof(int*)*graphMatrix->size);
16     }
17     
18     /* 图中所有元素赋值 */
19     for(i=0; i<graphMatrix->size; ++i){
20         for(j=0; j<graphMatrix->size; ++j){
21             graphMatrix->graph[i][j] = INT_MAX;
22         }
23     }
24     return graphMatrix;  /* 返回图结构体指针 */
25 }
26 
27 /* 读入图中顶点，权值 */
28 void ReadGraph(GraphMatrix* graphMatrix)
29 {
30     int vex1,vex2,weight;
31     printf("请输入顶点，顶点，权值，权值为0，则输入结束\n");
32     scanf("%d%d%d", &vex1, &vex2, &weight);
33     while(weight)
34     {
35         graphMatrix->graph[vex1][vex2] = weight;
36         scanf("%d%d%d", &vex1, &vex2, &weight);
37     }
38 }
39 
40 /* 输出图中顶点，权值  */
41 void WriteGraph(GraphMatrix* graphMatrix)
42 {
43     int i,j;
44     printf("图的结构如下，输出方式为顶点，顶点，权值\n");
45     for(i=0; i<graphMatrix->size; ++i){
46         for(j=0; j<graphMatrix->size; ++j){
47             if(graphMatrix->graph[i][j] < INT_MAX){
48                 printf("%d,%d,%d\n",i,j,graphMatrix->graph[i][j]);
49             }
50         }
51     }
52 }

源文件，graphmatrixutil.c

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #include "graphmatrixutil.h"
 4 int main()
 5 {
 6     GraphMatrix* graphMatrix = NULL;
 7     graphMatrix = InitGraph(4);
 8     ReadGraph(graphMatrix);
 9     WriteGraph(graphMatrix);
10     printf("\n");
11     return 0;
12 }

测试文件，main文件

　 2、邻接表（邻接链表），通过一个指针数组G[N]，存储图里面的所有顶点，顶点发出的边通过单链表存放，单链表的每个结点代表一条边 。顺序表存储的是n个顶点，链表存储的是与该顶点相邻的所有顶点表中的每个结点(含顶点域和指针域)；有向图，以某顶点为起点的数组表，是正邻接表，以某顶点为终点的数组表是逆邻接表。

  1 /* 图的邻接表表示法 */
  2  
  3 #define MaxVertexNum 100    /* 最大顶点数设为100 */
  4 typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
  5 typedef int WeightType;        /* 边的权值设为整型 */
  6 typedef char DataType;        /* 顶点存储的数据类型设为字符型 */
  7  
  8 /* 边的定义 */
  9 typedef struct ENode *PtrToENode;
 10 struct ENode{
 11     Vertex V1, V2;      /* 有向边<V1, V2> */
 12     WeightType Weight;  /* 权重 */
 13 };
 14 typedef PtrToENode Edge;
 15  
 16 /* 邻接点的定义 */
 17 typedef struct AdjVNode *PtrToAdjVNode; 
 18 struct AdjVNode{
 19     Vertex AdjV;        /* 邻接点下标 */
 20     WeightType Weight;  /* 边权重 */
 21     PtrToAdjVNode Next;    /* 指向下一个邻接点的指针 */
 22 };
 23  
 24 /* 顶点表头结点的定义 */
 25 typedef struct Vnode{
 26     PtrToAdjVNode FirstEdge;/* 边表头指针 */
 27     DataType Data;            /* 存顶点的数据 */
 28     /* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
 29 } AdjList[MaxVertexNum];    /* AdjList是邻接表类型 */
 30  
 31 /* 图结点的定义 */
 32 typedef struct GNode *PtrToGNode;
 33 struct GNode{  
 34     int Nv;     /* 顶点数 */
 35     int Ne;     /* 边数   */
 36     AdjList G;  /* 邻接表 */
 37 };
 38 typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
 39  
 40  
 41  
 42 LGraph CreateGraph( int VertexNum )
 43 { /* 初始化一个有VertexNum个顶点但没有边的图 */
 44     Vertex V;
 45     LGraph Graph;
 46      
 47     Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
 48     Graph->Nv = VertexNum;
 49     Graph->Ne = 0;
 50     /* 初始化邻接表头指针 */
 51     /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
 52        for (V=0; V<Graph->Nv; V++)
 53         Graph->G[V].FirstEdge = NULL;
 54              
 55     return Graph; 
 56 }
 57         
 58 void InsertEdge( LGraph Graph, Edge E )
 59 {
 60     PtrToAdjVNode NewNode;
 61      
 62     /* 插入边 <V1, V2> */
 63     /* 为V2建立新的邻接点 */
 64     NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
 65     NewNode->AdjV = E->V2;
 66     NewNode->Weight = E->Weight;
 67     /* 将V2插入V1的表头 */
 68     NewNode->Next = Graph->G[E->V1].FirstEdge;
 69     Graph->G[E->V1].FirstEdge = NewNode;
 70          
 71     /* 若是无向图，还要插入边 <V2, V1> */
 72     /* 为V1建立新的邻接点 */
 73     NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
 74     NewNode->AdjV = E->V1;
 75     NewNode->Weight = E->Weight;
 76     /* 将V1插入V2的表头 */
 77     NewNode->Next = Graph->G[E->V2].FirstEdge;
 78     Graph->G[E->V2].FirstEdge = NewNode;
 79 }
 80  
 81 LGraph BuildGraph()
 82 {
 83     LGraph Graph;
 84     Edge E;
 85     Vertex V;
 86     int Nv, i;
 87      
 88     scanf("%d", &Nv);   /* 读入顶点个数 */
 89     Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
 90      
 91     scanf("%d", &(Graph->Ne));   /* 读入边数 */
 92     if ( Graph->Ne != 0 ) { /* 如果有边 */ 
 93         E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ 
 94         /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
 95         for (i=0; i<Graph->Ne; i++) {
 96             scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
 97             /* 注意：如果权重不是整型，Weight的读入格式要改 */
 98             InsertEdge( Graph, E );
 99         }
100     } 
101  
102     /* 如果顶点有数据的话，读入数据 */
103     for (V=0; V<Graph->Nv; V++) 
104         scanf(" %c", &(Graph->G[V].Data));
105  
106     return Graph;
107 }

图的邻接表表示法

　头文件，源文件，动态分配一维指针数组，有向图

 1 /* 
 2     图的邻接表表示及辅助函数 
 3     graphlistutil.h
 4 */
 5 #include <stdio.h>
 6 #include <stdlib.h>
 7 
 8 #ifndef GRAPHLISTUTIL_H_
 9 #define GRAPHLISTUTIL_H_
10 
11 /* 图结点结构体 */
12 typedef struct GRAPHLISTNODE_STRU{
13     int nodeno; /* 结点的编号 */
14     struct GRAPHLISTNODE_STRU* next;
15 }GraphListNode;
16 
17 /* 图结构体 */
18 typedef struct GRAPHLIST_STRU{
19     int size;     /* 图中结点的个数 */
20     GraphListNode* graphListArray;   /* 图的邻接表 */
21 }GraphList;     /* 定义结构体类型 */
22 
23 /* 初始化图 */
24 GraphList* InitGraph(int num);
25 
26 /* 将数据读入图 */
27 void ReadGraph(GraphList* graphList);
28 
29 /* 将图的结构显示出来 */
30 void WriteGraph(GraphList* graphList);
31 
32 #endif

头文件，graphlistutil.h

 1 #include "graphListutil.h"
 2 
 3 /* 初始化图，num表示图中结点个数，邻接表表示图 */
 4 GraphList* InitGraph(int num)
 5 {
 6     int i;
 7     /* 图空间定义 */
 8     GraphList* graphList = (GraphList*)malloc(sizeof(GraphList));    
 9     graphList->size = num;/* 图中结点数 */
10     
11     /* 邻接表数组分配空间 */
12     graphList->graphListArray = (GraphListNode*)malloc(sizeof(GraphListNode)*graphList->size); 
13     /* 邻接表数组赋值 */
14     for(i=0; i<graphList->size; ++i){
15         graphList->graphListArray[i].next = NULL;
16         graphList->graphListArray[i].nodeno = i;
17     }
18     return graphList;  /* 返回图结构体指针 */
19 }
20 
21 /* 读入图中顶点 */
22 void ReadGraph(GraphList* graphList)
23 {
24     int vex1,vex2;
25     GraphListNode* tempNodePtr = NULL;
26     printf("请输入顶点，顶点，顶点为-1，则输入结束\n");
27     scanf("%d%d", &vex1, &vex2);
28     while(vex1>=0 && vex2>=0)
29     {
30         tempNodePtr = (GraphListNode*)malloc(sizeof(GraphListNode));
31         tempNodePtr->nodeno = vex2;
32         tempNodePtr->next = NULL;
33         tempNodePtr->next = graphList->graphListArray[vex1].next;
34         graphList->graphListArray[vex1].next = tempNodePtr;
35         scanf("%d%d", &vex1, &vex2);
36     }
37 }
38 
39 /* 输出图中顶点  */
40 void WriteGraph(GraphList* graphList)
41 {
42     int i;
43     GraphListNode* tempNodePtr = NULL;
44     printf("图的结构如下，输出方式为顶点，顶点\n");
45     for(i=0; i<graphList->size; ++i){
46         tempNodePtr = graphList->graphListArray[i].next;
47         while(tempNodePtr){           
48             printf("结点%d到结点%d有边相连\n",i,tempNodePtr->nodeno);         
49             tempNodePtr = tempNodePtr->next;
50         }
51     }
52 }

源文件，graphListutil.c

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #include "graphListutil.h"
 4 int main()
 5 {
 6     GraphList* graphList = NULL;
 7     graphList = InitGraph(4);
 8     ReadGraph(graphList);
 9     WriteGraph(graphList);
10     printf("\n");
11     return 0;
12 }

测试文件，main文件

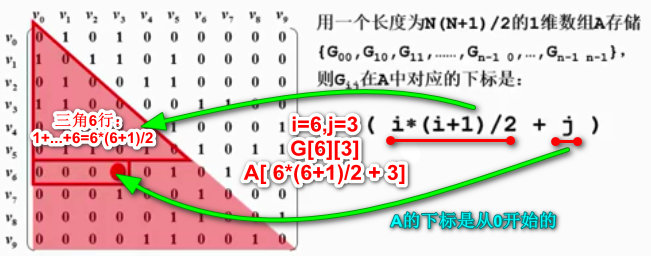
　　3、一维数组存储无向图的边：用一个长度为n*(n+1)/2的一维数组用来存储无向图的边，G_ij在数组中对应的下标是：(i*(i+1)/2 + j)

　　例，用一维数组A[ ]存储有4个顶点的无向图如下：A[ ] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }则顶点2和顶点0之间是否有边。

　　导入公式，2*(2+1)/2 + 0，一维数组的下标为3（i是行，j是列），A的下标3的值为1，可以判断，2和顶点0之间是有边的。

//n*(n+1)/2
邻接矩阵的下三角表示无向图（包含对角线），边共有：1 + 2 + 3 + 4 + 5 + ... + n
等差数列的和为：（首项 + 末项）* 项数 / 2，即 n*(n+1)/2 
公式推导：
令a=1+2+3+……+n
则a=n+……+3+2+1
两式相加
2a=(1+n)+[2+(n-1)]+……+[(n-1)+2]+(n+1)
=(n+1)+(n+1)+……+(n+1)+(n+1)
=n(n+1)
所以原式 = n*(n+1)/2
//Gij在数组中对应的下标是：(i*(i+1)/2 + j)
i*(i+1)/2的推导同上

/*图的邻接矩阵，算法7.2
借助邻接矩阵很容易判定任意两个顶点之间
是否有边（弧）相连，并容易求得各个顶点的度*/

#include <stdio.h>
#define MAXLEN 10

typedef struct
{
    char vexs[MAXLEN];//顶点向量，存储一串顶点标识
    int *edges;//表示两个顶点之间的关系 一维数组，下三角
    int n, e;
} MGraph;

//建立一个图的邻接矩阵存储的算法如下：
void CreateMGraph(MGraph &G)
{
    int i, j, k;
    char ch1, ch2;
    printf("请输入顶点数和边数:\n");
    scanf("%d%d", &(G.n), &(G.e));
    G.edges = new int[G.n*(G.n+1)/2];
    printf("请输入顶点标识（构造顶点向量）:\n");
    for(i = 0; i < G.n; i++)
    {
        getchar();
        scanf("%c", &(G.vexs[i]));
    }

    /*格式化，任意两顶点之间的关系置为0（fause）*/
    for(i = 0; i < G.n*(G.n+1)/2; i++)    
            G.edges[i] = 0;
        
    printf("初始化每条边的首尾:\n");
    for(k = 0; k < G.e; k++)
    {
        getchar();
        printf("请输入第%d条边的首尾顶点序号：\n", k + 1);
        scanf("%c%c", &ch1, &ch2);//注意输入时不要加空格
        for(i = 0; ch1 != G.vexs[i]; i++);  //找顶点ch1
        for(j = 0; ch2 != G.vexs[j]; j++);  //找顶点ch2
        
        if(i<j) //下三角，j应该小于等于i
        {
            int t = i;
            i=j;
            j=t;
        }
        G.edges[i*(i+1)/2+j] = 1;  //有向图 顶点ch1到顶点ch2
    }
}

int main()
{
    MGraph  M;
    CreateMGraph(M);
    int i, j;
    for(i=0; i<M.n; i++)
    {
        for(j=0; j<=i; j++) //下三角j小于等于i
        {

            printf("%c-->%c ", M.vexs[i], M.vexs[j]);
            if(M.edges[i*(i+1)/2+j])
                printf("Y  ");
            else
                printf("N  ");
        }
        printf("\n");
    }
    return 0;
}

View Code

三、图的遍历 深度优先搜索，广度优先搜索　

　　图的遍历，从图中某一顶点出发，访遍图中其余顶点，使每一个顶点被访问且仅被访问一次。图的遍历，是求图的连通性问题、拓扑问题、关键路径问题等的算法基础。图的遍历通常有两种方法：深度优先搜索，广度优先搜索。

　　1、深度优先搜索，类似于树的先根遍历，是树的先根遍历的推广。从图中某个顶点v出发，访问此顶点，然后依次从v的未被访问的邻接点出发深度优先遍历图, 直至所有与v有通路的顶点都被访问到；若此时图中还有顶点未被访问到，则另选图中未被访问的顶点作起点，重复上述过程，直到图中所有顶点都被访问到为止。深度优先搜索的序列不是唯一的。

　　邻接矩阵存储的图 - DFS - 1

 1 /* 邻接矩阵表示图，深度优先搜索 */
 2 #include <stdio.h>
 3 #include <stdlib.h>
 4 #include <limits.h>
 5 
 6 #define N 100  /* 图大小 */
 7 int G[N][N];   /* 邻接矩阵图G */
 8 int size;      /* 邻接矩阵图顶点个数 */
 9 int visited[N] = {0}; /* 顶点初始化没有被访问过 */
10 int u,v;       /* 顶点u顶点v */
11 bool tag = false; /* 记录是否可以从顶点u到达顶点v的标记 */
12 
13 /* 初始化邻接矩阵图 */
14 void InitGraph()  
15 {
16     int i,j;
17     for(i=0; i < size; ++i){
18         for(j=0; j < size; ++j){
19             G[i][j] = INT_MAX;
20         }
21     }
22 }
23 
24 /* 读入无向图*/
25 void ReadGraph()
26 {
27     int vex1,vex2,weight;
28     printf("请输入顶点，顶点，权值，权值为0，则输入结束\n");
29     scanf("%d%d%d", &vex1, &vex2, &weight);
30     while(weight)
31     {
32         G[vex1][vex2] = weight;
33         G[vex2][vex1] = weight;
34         scanf("%d%d%d", &vex1, &vex2, &weight);
35     }
36 }
37 
38 /* 深度优先搜索 */
39 void DFS(int i)
40 {
41     int j;
42     visited[i] = 1;
43     if(i==v){  /*如果找到了路径，返回*/            
44         tag = true;
45         return;
46     }    
47    
48     for(j=0; j < size; j++)
49     {   /* 两顶点有边且没有被访问过 */
50         if(G[i][j] != INT_MAX && !visited[j]){            
51             DFS(j);        
52         }          
53     }
54 }
55 
56 /* 
57 两个连通分量的图 
58   0-1-2-3
59   4-5
60 */
61 
62 /*  
63 6
64 0 1 1
65 1 2 1
66 2 3 1
67 4 5 1
68 0 0 0
69 */
70 
71 int main()
72 {
73     printf("请输入构建的图的顶点个数\n");
74     scanf("%d",&size);
75     InitGraph();  /* 初始化邻接矩阵图 */
76     
77     ReadGraph();   /*读入无向图*/
78     
79     printf("查找顶点u顶点v之间是否有路径，请输入顶点u、v\n");
80     scanf("%d%d",&u,&v);
81     DFS(u);
82     
83     if(tag)
84         printf("顶点%d顶点%d之间有路径\n",u,v);
85     else
86         printf("顶点%d顶点%d之间没有路径\n",u,v);
87     return 0;
88 }

邻接矩阵，dfs，判断图任意两顶点之间是否有路径

　　邻接矩阵存储的图 - DFS - 2

 1 #include <limits.h>
 2 #include <stdio.h>
 3 #include <stdlib.h>
 4 
 5 #ifndef GRAPHMATRIXUTIL_H_
 6 #define GRAPHMATRIXUTIL_H_
 7 
 8 /* 图结构体 */
 9 typedef struct GRAPHMATRIX_STRU{
10     int size;     /* 图中结点的个数 */
11     int **graph;   /* 二维数组指针 */
12 }GraphMatrix;     /* 定义结构体类型 */
13 
14 /* 初始化图 */
15 GraphMatrix* InitGraph(int num);
16 
17 /* 将数据读入图 */
18 void ReadGraph(GraphMatrix* graphMatrix);
19 
20 /* 将图的结构显示出来 */
21 void WriteGraph(GraphMatrix* graphMatrix);
22 
23 /*DFS*/
24 void DFS(GraphMatrix* graphMatrix, int *visited, int i);
25 
26 /*DFSGraphMatrix*/
27 void DFSGraphMatrix(GraphMatrix* graphMatrix);
28 #endif

邻接矩阵，dfs_graphmatrix.h

 1 #include "dfs_graphmatrix.h"
 2 
 3 /* 
 4     图的深度优先递归算法,邻接矩阵表示图 
 5     graphMatrix 图
 6     visited 做访问标记的一维数组
 7     i 结点编号
 8 */
 9 /* 初始化图，num表示图中结点个数，邻接矩阵表示图 */
10 GraphMatrix* InitGraph(int num)
11 {
12     int i,j;
13     /* 图空间定义 */
14     GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix));    
15     graphMatrix->size = num;/* 图中结点数 */
16     
17     /* 指针数组分配空间 */
18     graphMatrix->graph = (int**)malloc(sizeof(int*)*graphMatrix->size);
19     /* 指针数组中的指针分配空间 */
20     for(i=0; i<graphMatrix->size; ++i){
21         graphMatrix->graph[i] = (int*)malloc(sizeof(int*)*graphMatrix->size);
22     }
23     
24     /* 图中所有元素赋值 */
25     for(i=0; i<graphMatrix->size; ++i){
26         for(j=0; j<graphMatrix->size; ++j){
27             graphMatrix->graph[i][j] = INT_MAX;
28         }
29     }
30     return graphMatrix;  /* 返回图结构体指针 */
31 }
32 
33 /* 读入图中顶点，权值 */
34 void ReadGraph(GraphMatrix* graphMatrix)
35 {
36     int vex1,vex2,weight;
37     printf("请输入顶点，顶点，权值，权值为0，则输入结束\n");
38     scanf("%d%d%d", &vex1, &vex2, &weight);
39     while(weight)
40     {
41         graphMatrix->graph[vex1][vex2] = weight;
42         scanf("%d%d%d", &vex1, &vex2, &weight);
43     }
44 }
45 
46 /* 输出图中顶点，权值  */
47 void WriteGraph(GraphMatrix* graphMatrix)
48 {
49     int i,j;
50     printf("图的结构如下，输出方式为顶点，顶点，权值\n");
51     for(i=0; i<graphMatrix->size; ++i){
52         for(j=0; j<graphMatrix->size; ++j){
53             if(graphMatrix->graph[i][j] < INT_MAX){
54                 printf("%d,%d,%d\n",i,j,graphMatrix->graph[i][j]);
55             }
56         }
57     }
58 }
59 
60 void DFS(GraphMatrix* graphMatrix, int *visited, int i)
61 {
62     int j;
63     visited[i] = 1;
64     printf("%d ", i);
65     for(j=0; j < graphMatrix->size; j++)
66     {
67         if(graphMatrix->graph[i][j] != INT_MAX && !visited[j])
68             DFS(graphMatrix,visited,j);
69     }
70 }
71 
72 void DFSGraphMatrix(GraphMatrix* graphMatrix)
73 {
74     int i;
75     /* 定义,用以记录顶点是否被访问的数组visited */
76     int *visited = (int*)malloc(sizeof(int)*graphMatrix->size);
77 
78     for(i=0; i < graphMatrix->size; ++i)
79         visited[i] = 0;    /* 初始化顶点都没有被访问 */
80 
81     for(i=0; i < graphMatrix->size; ++i)
82         if(!visited[i])  /* 对未访问的顶点调用DFS,若是连通图,只会执行一次 */
83             DFS(graphMatrix,visited,i);
84 }

邻接矩阵，dfs_graphmatrix.c

 1 /*
 2 0 1 1
 3 1 0 1
 4 0 2 1
 5 2 0 1
 6 0 3 1
 7 3 0 1
 8 1 2 1
 9 2 1 1
10 1 3 1
11 3 1 1
12 0 0 0
13 */
14 #include <stdio.h>
15 #include <stdlib.h>
16 #include "dfs_graphmatrix.h"
17 
18 int main()
19 {
20     GraphMatrix* graphMatrix = NULL;
21     graphMatrix = InitGraph(4);
22     ReadGraph(graphMatrix);
23     /*WriteGraph(graphMatrix);*/
24     DFSGraphMatrix(graphMatrix); /*深度优先搜索*/
25     printf("\n");
26     return 0;
27 }

测试文件，main文件

　　邻接表存储的图 - DFS - 1

 1 /* 
 2     图的邻接表表示及辅助函数 
 3     graphlist.h
 4 */
 5 #include <stdio.h>
 6 #include <stdlib.h>
 7 
 8 #ifndef GRAPHLIST_H_
 9 #define GRAPHLIST_H_
10 
11 /* 图结点结构体 */
12 typedef struct GRAPHLISTNODE_STRU{
13     int nodeno; /* 结点的编号 */
14     struct GRAPHLISTNODE_STRU* next;
15 }GraphListNode;
16 
17 /* 图结构体 */
18 typedef struct GRAPHLIST_STRU{
19     int size;     /* 图中结点的个数 */
20     GraphListNode* graphListArray;   /* 图的邻接表 */
21 }GraphList;     /* 定义结构体类型 */
22 
23 /* 初始化图 */
24 GraphList* InitGraph(int num);
25 
26 /* 将数据读入图 */
27 void ReadGraph(GraphList* graphList);
28 
29 /* 将图的结构显示出来 */
30 void WriteGraph(GraphList* graphList);
31 /*DFS*/
32 void DFS(GraphList* graphList, int *visited, int i);
33 
34 /*DFSGraphList*/
35 void DFSGraphList(GraphList* graphMatrix);
36 #endif

邻接表，graphlist.h

 1 #include "dfs_graphlist.h"
 2 
 3 /* 
 4     图的深度优先递归算法,邻接表表示图 
 5     graphList 图
 6     visited 做访问标记的一维数组
 7     i 结点编号
 8 */
 9 
10 /* 初始化图，num表示图中结点个数，邻接表表示图 */
11 GraphList* InitGraph(int num)
12 {
13     int i;
14     /* 图空间定义 */
15     GraphList* graphList = (GraphList*)malloc(sizeof(GraphList));    
16     graphList->size = num;/* 图中结点数 */
17     
18     /* 邻接表数组分配空间 */
19     graphList->graphListArray = (GraphListNode*)malloc(sizeof(GraphListNode)*graphList->size); 
20     /* 邻接表数组赋值 */
21     for(i=0; i<graphList->size; ++i){
22         graphList->graphListArray[i].next = NULL;
23         graphList->graphListArray[i].nodeno = i;
24     }
25     return graphList;  /* 返回图结构体指针 */
26 }
27 
28 /* 读入图中顶点 */
29 void ReadGraph(GraphList* graphList)
30 {
31     int vex1,vex2;
32     GraphListNode* tempNodePtr = NULL;
33     printf("请输入顶点，顶点，顶点为-1，则输入结束\n");
34     scanf("%d%d", &vex1, &vex2);
35     while(vex1>=0 && vex2>=0)
36     { /*表结点*/
37         tempNodePtr = (GraphList*)malloc(sizeof(GraphListNode));
38         tempNodePtr->nodeno = vex2;
39         tempNodePtr->next = NULL;
40         /*头插法*/
41         tempNodePtr->next = graphList->graphListArray[vex1].next;
42         graphList->graphListArray[vex1].next = tempNodePtr;
43         scanf("%d%d", &vex1, &vex2);
44     }
45 }
46 
47 /* 输出图中顶点  */
48 void WriteGraph(GraphList* graphList)
49 {
50     int i;
51     GraphListNode* tempNodePtr = NULL;
52     printf("图的结构如下，输出方式为顶点，顶点\n");
53     for(i=0; i<graphList->size; ++i){
54         tempNodePtr = graphList->graphListArray[i].next;
55         while(tempNodePtr){           
56             printf("结点%d到结点%d有边相连\n",i,tempNodePtr->nodeno);         
57             tempNodePtr = tempNodePtr->next;
58         }
59     }
60 }
61 
62 void DFS(GraphList* graphList, int *visited, int i)
63 {
64     int j;
65     GraphListNode* tempNodePtr = NULL;
66     visited[i] = 1;
67     printf("%d ",i);
68     
69     tempNodePtr = graphList->graphListArray[i].next;
70     while(tempNodePtr)
71     {
72         if(!visited[tempNodePtr->nodeno])
73             DFS(graphList,visited,tempNodePtr->nodeno);
74         tempNodePtr = tempNodePtr->next;
75     }
76 }
77 
78 void DFSGraphList(GraphList* graphList)
79 {
80     int i;
81     /* 定义,用以记录顶点是否被访问的数组visited */
82     int *visited = (int*)malloc(sizeof(int)*graphList->size);
83 
84     for(i=0; i < graphList->size; ++i)
85         visited[i] = 0;    /* 初始化顶点都没有被访问 */
86 
87     for(i=0; i < graphList->size; ++i)
88         if(!visited[i])  /* 对未访问的顶点调用DFS,若是连通图,只会执行一次 */
89             DFS(graphList,visited,i);
90 }

邻接表，graphlist.c

 1 /*
 2 0 3
 3 0 2
 4 0 1
 5 1 3
 6 1 2
 7 1 0
 8 2 1
 9 2 0
10 3 0
11 3 1
12 -1 -1
13 */
14 #include <stdio.h>
15 #include <stdlib.h>
16 #include "dfs_graphlist.h"
17 
18 int main()
19 {
20     GraphList* graphList = NULL;
21     graphList = InitGraph(4);
22     ReadGraph(graphList);
23     /*WriteGraph(graphList);*/
24     DFSGraphList(graphList); /*深度优先搜索*/
25     printf("\n");
26     return 0;
27 }

测试文件，main文件

　　邻接表存储的图 - DFS - 2

 1 /* 邻接表存储的图 - DFS */
 2  
 3 void Visit( Vertex V )
 4 {
 5     printf("正在访问顶点%d\n", V);
 6 }
 7  
 8 /* Visited[]为全局变量，已经初始化为false */
 9 void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
10 {   /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */
11     PtrToAdjVNode W;
12      
13     Visit( V ); /* 访问第V个顶点 */
14     Visited[V] = true; /* 标记V已访问 */
15  
16     for( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
17         if ( !Visited[W->AdjV] )    /* 若W->AdjV未被访问 */
18             DFS( Graph, W->AdjV, Visit );    /* 则递归访问之 */
19 }

邻接表存储的图 - DFS

　　2、 广度优先搜索，类似于树的层次遍历，从图的某个顶点v出发，在访问了v之后，依次访问v的各个未曾被访问的邻接点，直至图中所有已被访问的顶点的邻接点都被访问到。若图中还有未被访问的顶点，则任选其中之一作为起点，重新开始上述过程，直至图中所有顶点都被访问到。

　　邻接矩阵存储的图 - BFS - 1

 1 #ifndef PLINKLQUEUE_H
 2 #define PLINKLQUEUE_H
 3 
 4 #include <stdio.h>
 5 #include <stdlib.h>
 6 
 7 typedef int DataType;
 8 
 9 struct Node
10 {
11     DataType data;
12     struct Node    *link;
13 };
14 typedef struct Node *PNode;
15 
16 struct Queue
17 {    PNode        f;
18     PNode        r;
19 };
20 typedef struct Queue *LinkQueue;
21 
22 LinkQueue SetNullQueue_Link();
23 int IsNullQueue_Link(LinkQueue lqueue);
24 void EnQueue_link(LinkQueue lqueue, DataType x);
25 void DeQueue_link(LinkQueue lqueue);
26 DataType  FrontQueue_link(LinkQueue lqueue);
27 
28 #endif

链队列，LinkQueue.h

 1 #include "LinkQueue.h"
 2 
 3 LinkQueue  SetNullQueue_Link()
 4 { 
 5     LinkQueue lqueue;
 6     lqueue = (LinkQueue)malloc(sizeof(struct Queue));
 7     if (lqueue != NULL)
 8     {    
 9         lqueue->f = NULL;
10         lqueue->r = NULL;
11     }
12        else    
13         printf("Alloc failure! \n");
14     return  lqueue;
15  }
16 
17 int IsNullQueue_Link(LinkQueue lqueue)
18 {        
19     return (lqueue->f == NULL);
20 }
21 
22 void EnQueue_link(LinkQueue lqueue, DataType x)
23 {     
24     PNode  p;
25     p = (PNode)malloc(sizeof(struct Node));
26     if (p == NULL)
27         printf("Alloc failure!");
28     else{    
29             p->data = x;
30             p->link = NULL;
31             if (lqueue->f == NULL) //空队列的特殊处理
32             {     
33                 lqueue->f = p;
34                 lqueue->r = p;
35             }
36               else
37             {     
38                 lqueue->r->link = p;
39                 lqueue->r = p;
40             }
41         }
42 } 
43 
44 void DeQueue_link(LinkQueue lqueue)
45 {    
46     struct Node  * p;
47     if (lqueue->f == NULL)
48         printf( "It is empty queue!\n ");
49       else
50     {     
51         p = lqueue->f;
52         lqueue->f = lqueue->f->link;
53         free(p);
54     }
55 }
56 
57 DataType  FrontQueue_link(LinkQueue lqueue)
58 {           
59     if (lqueue->f == NULL)
60     {
61         printf("It is empty queue!\n");
62         return 0;
63     }
64     else
65         return (lqueue->f->data);
66 }

链队列，LinkQueue.c

 1 /** 
 2 * @file graphmatrixutil.h
 3 * @brief 图的邻接矩阵表示以及辅助函数                                                               
 4 */
 5 
 6 #ifndef GRAPHMATRIXUTIL_H_
 7 #define GRAPHMATRIXUTIL_H_
 8 #include <stdlib.h>
 9 #include <stdio.h>
10 #include <limits.h>
11 /**
12  * @brief 图的邻接矩阵表示
13  */
14 typedef struct    GRAPHMATRIX_STRU
15 {
16     int size;/*!< 图中结点的个数 */
17     int **graph;/*!<二维数组保存图 */
18 }GraphMatrix;
19 
20 /**
21   * @brief  初始化图
22   * @param[in]   num    图中结点的个数
23   * @return    用邻接矩阵表示的图
24   */
25 GraphMatrix* InitGraph(int num);
26 
27 /**
28   * @brief  将数据读入图中
29   * @param[in]   graphMatrix    图
30   */
31 void ReadGraph(GraphMatrix* graphMatrix);
32 
33 /**
34   * @brief  将图的结构显示出来
35   * @param[in]   graphMatrix    图
36   */
37 void WriteGraph(GraphMatrix* graphMatrix);
38 
39 #endif

邻接矩阵，graphmatrixutil.h

 1 /** 
 2 * @file graphmatrixutil.c
 3 * @brief 图的邻接矩阵表示以及辅助函数                                                               
 4 */
 5 
 6 #include "graphmatrixutil.h"
 7 
 8 /**
 9   * @brief  初始化图
10   * @param[in]   num    图中结点的个数
11   * @return    用邻接矩阵表示的图
12   */
13 GraphMatrix* InitGraph(int num)
14 {
15     int i;
16     int j;
17     GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix));
18     /** 图中结点的个数 */
19     graphMatrix->size = num;
20     /** 给图分配空间 */
21     graphMatrix->graph = (int**)malloc(sizeof(int*) * graphMatrix->size);
22     for (i=0;i<graphMatrix->size;i++)
23     {
24         graphMatrix->graph[i] = (int*)malloc(sizeof(int) * graphMatrix->size);
25     }
26 
27     /** 给图中所有元素设置初值 */
28     for (i=0;i<graphMatrix->size;i++)
29     {
30         for(j=0;j<graphMatrix->size;j++)
31         {
32             graphMatrix->graph[i][j]=INT_MAX;
33         }
34     }
35 
36     return graphMatrix;
37 }
38 
39 /**
40   * @brief  将数据读入图中,方式为点 点  权值，如果输入的权值为0，则输入结束
41   * @param[in]   graphMatrix    图
42   */
43 void ReadGraph(GraphMatrix* graphMatrix)
44 {
45     int vex1, vex2, weight;
46 
47     /** 输入方式为点 点 权值，权值为0，则输入结束 */
48     printf("请输入，输入方式为点 点 权值，权值为0，则输入结束\n");
49     scanf("%d%d%d", &vex1, &vex2, &weight);
50 
51     while(weight != 0)
52     {
53         graphMatrix->graph[vex1][vex2] = weight;
54         scanf("%d%d%d", &vex1, &vex2, &weight);
55     }
56 }
57 
58 /**
59   * @brief  将图的结构显示出来,输出方式为点， 点， 权值
60   * @param[in]   graphMatrix    图
61   */
62 void WriteGraph(GraphMatrix* graphMatrix)
63 {
64     int i, j;
65 
66     printf("图的结构如下，输出方式为点 ，点 ，权值\n");
67     for (i=0;i<graphMatrix->size; i++)
68     {
69         for (j=0; j<graphMatrix->size; j++)
70         {
71             if (graphMatrix->graph[i][j] < INT_MAX)
72             {
73                 printf("%d,%d,%d\n", i, j, graphMatrix->graph[i][j]);
74             }
75         }
76     }
77 }

邻接矩阵，graphmatrixutil.c

 1 /** 
 2 * @file bfs_graphmatrix.h
 3 * @brief 图的广度优先遍历，邻接矩阵表示图                                                              
 4 */
 5 #ifndef BFS_GRAPHMATRIX_H_
 6 #define BFS_GRAPHMATRIX_H_
 7 
 8 #include "graphmatrixutil.h"
 9 #include "LinkQueue.h"
10 
11 /**
12   * @brief  图的广度优先遍历递归算法，邻接矩阵表示图
13   * @param[in]   graphMatrix    图
14   * @param[in]   visited    做标记的（设置点是否被访问）一维数组
15   * @param[in]   i    结点编号
16   */
17 void BFS(GraphMatrix* graphMatrix, int * visited, int i);
18 
19 /**
20   * @brief  图的广度优先遍历，邻接矩阵表示图
21   * @param[in]   graphMatrix    图
22   */
23 void BFSGraphMatrix(GraphMatrix* graphMatrix);
24 
25 
26 #endif

邻接矩阵，bfs_graphmatrix.h

 1 #include "bfs_graphmatrix.h"
 2 
 3 void BFS(GraphMatrix* graphMatrix, int * visited, int i)
 4 {
 5     int j;
 6     int tempVex;
 7     
 8     LinkQueue waitingQueue = NULL;
 9     waitingQueue = SetNullQueue_Link();
10     
11     /** 如果没有访问过，则访问 */
12     if (!visited[i])    
13     {
14         /** 设置标记，表明已经被访问 */
15         visited[i] = 1;    
16         /** 输出访问的结点编号 */
17         printf("%d ", i);
18         /** 将刚访问的结点放入队列 */
19         EnQueue_link(waitingQueue,i);
20         while(!IsNullQueue_Link(waitingQueue))    
21         {
22             tempVex = FrontQueue_link(waitingQueue);
23             DeQueue_link(waitingQueue);
24             for(j=0;j<graphMatrix->size;j++) 
25             { 
26                 if(graphMatrix->graph[tempVex][j] != INT_MAX && !visited[j])
27                 {
28                     visited[j] = 1;
29                     EnQueue_link(waitingQueue,j);
30                     printf("%d ", j);
31                 }
32             } 
33         }
34     }
35 }
36 
37 void BFSGraphMatrix(GraphMatrix* graphMatrix)
38 {
39     int i;
40     
41     /** 用于记录图中哪些结点已经被访问了 */
42     int *visited = (int*)malloc(sizeof(int) * graphMatrix->size);
43     
44     /** 设置所有结点都没有被访问，其中1为访问过，0为没有被访问 */
45     for(i = 0; i < graphMatrix->size; i++)
46         visited[i] = 0;
47     
48     /** 从0号结点开始进行广度优先遍历 */
49     for(i = 0; i < graphMatrix->size; i++)  
50     {
51         BFS(graphMatrix, visited, i);
52     }
53 }

邻接矩阵，bfs_graphmatrix.c

 1 /** 
 2 * @file graphmatrixutil.h
 3 * @brief 图的邻接矩阵表示以及辅助函数                                                               
 4 */
 5 
 6 #ifndef GRAPHMATRIXUTIL_H_
 7 #define GRAPHMATRIXUTIL_H_
 8 #include <stdlib.h>
 9 #include <stdio.h>
10 #include <limits.h>
11 /**
12  * @brief 图的邻接矩阵表示
13  */
14 typedef struct    GRAPHMATRIX_STRU
15 {
16     int size;/*!< 图中结点的个数 */
17     int **graph;/*!<二维数组保存图 */
18 }GraphMatrix;
19 
20 /**
21   * @brief  初始化图
22   * @param[in]   num    图中结点的个数
23   * @return    用邻接矩阵表示的图
24   */
25 GraphMatrix* InitGraph(int num);
26 
27 /**
28   * @brief  将数据读入图中
29   * @param[in]   graphMatrix    图
30   */
31 void ReadGraph(GraphMatrix* graphMatrix);
32 
33 /**
34   * @brief  将图的结构显示出来
35   * @param[in]   graphMatrix    图
36   */
37 void WriteGraph(GraphMatrix* graphMatrix);
38 
39 #endif

邻接矩阵，dfs_graphmatrix.h

 1 /** 
 2 * @file dfs_graphmatrix.cpp
 3 * @brief 图的深度优先遍历算法，用邻接矩阵表示的图                                                          
 4 */
 5 
 6 #include "dfs_graphmatrix.h"
 7 
 8 
 9 /**
10   * @brief  图的深度优先遍历递归算法，邻接矩阵表示图
11   * @param[in]   graphMatrix    图
12   * @param[in]   visited    做标记的（设置点是否被访问）一维数组
13   * @param[in]   i    结点编号
14   */
15 void DFS(GraphMatrix* graphMatrix, int * visited, int i)
16 {
17     int j;
18     visited[i] = 1;
19     printf("%d ", i);
20 
21     for(j = 0; j < graphMatrix->size; j++)
22     {
23         if(graphMatrix->graph[i][j] != INT_MAX && !visited[j])
24             DFS(graphMatrix, visited, j);
25     }
26 }
27 
28 /**
29   * @brief  深度遍历，邻接矩阵表示图
30   * @param[in]   graphMatrix    图
31   */
32 void DFSGraphMatrix(GraphMatrix* graphMatrix)
33 {
34     int i;
35     /** 用于记录图中哪些结点已经被访问了 */
36     int *visited = (int*)malloc(sizeof(int) * graphMatrix->size);
37 
38     /** 初始化为点都没有被访问 */
39     for(i = 0; i < graphMatrix->size; i++)
40         visited[i] = 0; 
41 
42     for(i = 0; i < graphMatrix->size; i++)
43         if(!visited[i]) /* 对未访问过的顶点调用DFS，若是连通图，只会执行一次 */ 
44             DFS(graphMatrix, visited, i);
45 }

邻接矩阵，dfs_graphmatrix.c

　　邻接矩阵存储的图 - BFS - 2

 1 /* 邻接矩阵存储的图 - BFS */
 2  
 3 /* IsEdge(Graph, V, W)检查<V, W>是否图Graph中的一条边，即W是否V的邻接点。  */
 4 /* 此函数根据图的不同类型要做不同的实现，关键取决于对不存在的边的表示方法。*/
 5 /* 例如对有权图, 如果不存在的边被初始化为INFINITY, 则函数实现如下:         */
 6 bool IsEdge( MGraph Graph, Vertex V, Vertex W )
 7 {
 8     return Graph->G[V][W]<INFINITY ? true : false;
 9 }
10  
11 /* Visited[]为全局变量，已经初始化为false */
12 void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) )
13 {   /* 以S为出发点对邻接矩阵存储的图Graph进行BFS搜索 */
14     Queue Q;     
15     Vertex V, W;
16  
17     Q = CreateQueue( MaxSize ); /* 创建空队列, MaxSize为外部定义的常数 */
18     /* 访问顶点S：此处可根据具体访问需要改写 */
19     Visit( S );
20     Visited[S] = true; /* 标记S已访问 */
21     AddQ(Q, S); /* S入队列 */
22      
23     while ( !IsEmpty(Q) ) {
24         V = DeleteQ(Q);  /* 弹出V */
25         for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
26             /* 若W是V的邻接点并且未访问过 */
27             if ( !Visited[W] && IsEdge(Graph, V, W) ) {
28                 /* 访问顶点W */
29                 Visit( W );
30                 Visited[W] = true; /* 标记W已访问 */
31                 AddQ(Q, W); /* W入队列 */
32             }
33     } /* while结束*/
34 }

邻接矩阵存储的图 - BFS

　　邻接表存储的图 - BFS

 1 /** 
 2 * @file graphlistutil.h
 3 * @brief 图的邻接表表示以及辅助函数                                                               
 4 */
 5 #ifndef GRAPHLISTUTIL_H
 6 #define GRAPHLISTUTIL_H
 7 #include <stdlib.h>
 8 #include <stdio.h>
 9 
10 typedef struct    GRAPHLISTNODE_STRU
11 {
12     int nodeno;/*!< 图中结点的编号 */
13     struct    GRAPHLISTNODE_STRU* next;/*!<指向下一个结点的指针 */
14 }GraphListNode;
15 
16 typedef struct    GRAPHLIST_STRU
17 {
18     int size;/*!< 图中结点的个数 */
19     GraphListNode* graphListArray;/*!<图的邻接表 */
20 }GraphList;
21 
22 /**
23   * @brief  初始化图
24   * @param[in]   num    图中结点的个数
25   * @return    用邻接表表示的图
26   */
27 GraphList* InitGraph(int num);
28 
29 /**
30   * @brief  将数据读入图中
31   * @param[in]   graphList    图
32   */
33 void ReadGraph(GraphList* graphList);
34 
35 /**
36   * @brief  将图的结构显示出来
37   * @param[in]   graphList    图
38   */
39 void WriteGraph(GraphList* graphList);
40 
41 #endif

邻接表，graphlistutil.h

 1 /** 
 2 * @file graphlistutil.c
 3 * @brief 图的邻接表表示以及辅助函数                                                               
 4 */
 5 #include "graphlistutil.h"
 6 
 7 /**
 8   * @brief  初始化图
 9   * @param[in]   num    图中结点的个数
10   * @return    用邻接表表示的图
11   */
12 GraphList* InitGraph(int num)
13 {
14     int i;
15     GraphList *graphList = (GraphList *)malloc(sizeof(GraphList));
16 
17     graphList->size = num;
18     graphList->graphListArray = (GraphListNode*)malloc(sizeof(GraphListNode)*num);
19 
20     for (i=0; i<num; i++)
21     {
22         graphList->graphListArray[i].next = NULL;
23         graphList->graphListArray[i].nodeno = i;
24     }
25 
26     return graphList;
27 }
28 
29 void ReadGraph(GraphList* graphList)
30 {
31     int vex1, vex2;
32     GraphListNode *tempNode = NULL;
33     printf("请输入，输入方式为点 点 ，点为-1，则输入结束\n");
34     scanf("%d%d", &vex1, &vex2);
35     while(vex1>=0 && vex2>=0)
36     {
37         tempNode = (GraphListNode*)malloc(sizeof(GraphListNode));
38         tempNode->nodeno = vex2;
39         tempNode->next = NULL;
40         /*尾插*/
41         tempNode->next = graphList->graphListArray[vex1].next;
42         graphList->graphListArray[vex1].next = tempNode;
43         scanf("%d%d", &vex1, &vex2);
44     }
45 }
46 
47 void WriteGraph(GraphList* graphList)
48 {
49     int i;
50     GraphListNode *tempNode = NULL;
51     for (i=0; i<graphList->size; i++)
52     {
53         tempNode = graphList->graphListArray[i].next;
54         while(tempNode != NULL)
55         {
56             printf("结点%d和%d相连\n",i,tempNode->nodeno);
57             tempNode = tempNode->next;
58         }
59     }
60 }

邻接表，graphlistutil.cpp

 1 /** 
 2 * @file bfs_graphlist.h
 3 * @brief 图的广度优先遍历，邻接表表示图                                                              
 4 */
 5 #ifndef BFS_GRAPHLIST_H
 6 #define BFS_GRAPHLIST_H
 7 
 8 #include "graphlistutil.h"
 9 #include <stdio.h>
10 #include <stdlib.h>
11 #include <queue>
12 /**
13   * @brief  图的广度优先遍历递归算法，邻接表表示图
14   * @param[in]   graphList    图
15   * @param[in]   visited    做标记的（设置点是否被访问）一维数组
16   * @param[in]   i    结点编号
17   */
18 void BFS(GraphList* graphList, int * visited, int i);
19 
20 /**
21   * @brief  图的广度优先遍历，邻接表表示图
22   * @param[in]   graphList    图
23   */
24 void BFSGraphList(GraphList* graphList);
25 
26 #endif

邻接表，bfs_graphlist.h

 1 /** 
 2 * @file bfs_graphlist.cpp
 3 * @brief 图的广度优先遍历算法，用邻接表表示的图                                                          
 4 */
 5 
 6 #include "bfs_graphlist.h"
 7 using namespace std;
 8 
 9 void BFS(GraphList* graphList, int * visited, int i)
10 {
11     int tempVex;
12     GraphListNode *tempNode = NULL;
13     /** 广度优先遍历使用的队列是c++的STL中的queue */
14     queue<int> waitingQueue;
15 
16     /** 如果没有访问过，则访问 */
17     if (!visited[i])    
18     {
19         /** 设置标记，表明已经被访问 */
20         visited[i] = 1;    
21         /** 输出访问的结点编号 */
22         printf("%d ", i);
23         /** 将刚访问的结点放入队列 */
24         waitingQueue.push(i);
25 
26         /** 访问结点－广度优先 */
27         while(!waitingQueue.empty())    
28         {
29             tempVex = waitingQueue.front();
30             waitingQueue.pop();
31             tempNode = graphList->graphListArray[tempVex].next;
32             while(tempNode != NULL)
33             {
34                 if(!visited[tempNode->nodeno]) 
35                 { 
36                     visited[tempNode->nodeno] = 1;
37                     waitingQueue.push(tempNode->nodeno);
38                     printf("%d ", tempNode->nodeno);
39                 }
40                 tempNode = tempNode->next;
41             }
42         }
43     }
44 }
45 
46 
47 void BFSGraphList(GraphList* graphList)
48 {
49     int i;
50 
51     /** 用于记录图中哪些结点已经被访问了 */
52     int *visited = (int*)malloc(sizeof(int) * graphList->size);
53 
54     /** 设置所有结点都没有被访问，其中1为访问过，0为没有被访问 */
55     for(i = 0; i < graphList->size; i++)
56         visited[i] = 0;
57 
58     /** 从0号结点开始进行广度优先遍历 */
59     for(i = 0; i < graphList->size; i++)  
60     {
61         BFS(graphList, visited, i);
62     }
63 }

邻接表，bfs_graphlist.cpp

 1 /** 
 2 * @file dfs_graphlist.h
 3 * @brief 图的深度优先遍历，邻接表表示图                                                              
 4 */
 5 
 6 #ifndef DFS_GRAPHLIST_H
 7 #define DFS_GRAPHLIST_H
 8 
 9 #include "graphlistutil.h"
10 #include <stdio.h>
11 #include <stdlib.h>
12 /**
13   * @brief  图的深度优先遍历递归算法，邻接表表示图
14   * @param[in]   graphList    图
15   * @param[in]   visited    做标记的（设置点是否被访问）一维数组
16   * @param[in]   i    结点编号
17   */
18 void DFS(GraphList* graphList, int * visited, int i);
19 
20 /**
21   * @brief  深度遍历，邻接表表示图
22   * @param[in]   graphList    图
23   */
24 void DFSGraphList(GraphList* graphList);
25 
26 #endif

邻接表，dfs_graphlist.h

 1 /** 
 2 * @file dfs_graphlist.cpp
 3 * @brief 图的深度优先遍历算法，用邻接表表示的图                                                          
 4 */
 5 
 6 #include "dfs_graphlist.h"
 7 
 8 
 9 /**
10   * @brief  图的深度优先遍历递归算法，邻接表表示图
11   * @param[in]   graphList    图
12   * @param[in]   visited    做标记的（设置点是否被访问）一维数组
13   * @param[in]   i    结点编号
14   */
15 void DFS(GraphList* graphList, int * visited, int i)
16 {
17     //int j;
18     GraphListNode *tempNode = NULL;
19     visited[i] = 1;
20     printf("%d ", i);
21 
22     //for(j = 0; j < graphList->size; j++)
23     tempNode = graphList->graphListArray[i].next;
24     while(tempNode != NULL)
25     {
26         if(!visited[tempNode->nodeno])
27             DFS(graphList, visited, tempNode->nodeno);
28         tempNode = tempNode->next;
29     }
30 }
31 
32 /**
33   * @brief  深度遍历，邻接表表示图
34   * @param[in]   graphList    图
35   */
36 void DFSGraphList(GraphList* graphList)
37 {
38     int i;
39     /** 用于记录图中哪些结点已经被访问了 */
40     int *visited = (int*)malloc(sizeof(int) * graphList->size);
41 
42     /** 初始化为点都没有被访问 */
43     for(i = 0; i < graphList->size; i++)
44         visited[i] = 0; 
45 
46     for(i = 0; i < graphList->size; i++)
47         if(!visited[i]) /* 对未访问过的顶点调用DFS，若是连通图，只会执行一次 */ 
48             DFS(graphList, visited, i);
49 }

邻接表，dfs_graphlist.cpp

四、最短路径问题，在网络中，求两个不同顶点之间的所有路径中，边的权值之和最小的那一条路径，这条路径就是两点之间的最短路径，第一个顶点为源点，最后一个顶点为终点；

　　1、单源最短路径问题：从某固定源点出发，求其到所有其他顶点的最短路径（有权图，无权图）；

/* 邻接表存储 - 无权图的单源最短路算法 */
 
/* dist[]和path[]全部初始化为-1 */
void Unweighted ( LGraph Graph, int dist[], int path[], Vertex S )
{
    Queue Q;
    Vertex V;
    PtrToAdjVNode W;
     
    Q = CreateQueue( Graph->Nv ); /* 创建空队列, MaxSize为外部定义的常数 */
    dist[S] = 0; /* 初始化源点 */
    AddQ (Q, S);
 
    while( !IsEmpty(Q) ){
        V = DeleteQ(Q);
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
            if ( dist[W->AdjV]==-1 ) { /* 若W->AdjV未被访问过 */
                dist[W->AdjV] = dist[V]+1; /* W->AdjV到S的距离更新 */
                path[W->AdjV] = V; /* 将V记录在S到W->AdjV的路径上 */
                AddQ(Q, W->AdjV);
            }
    } /* while结束*/
}

邻接表存储，无权图单源最短路径算法

　　迪杰斯特拉Dijkstra算法（贪心算法），不适用负权图（当前还不存在，找出从s到一个顶点的路径，比找出从s到所有顶点的路径，更快的算法），这是按路径长度递增的次序产生最短路径的算法

　　代码1

 1 /* 
 2     graphmatrixutil.h                                                       
 3 */
 4 
 5 #ifndef GRAPHMATRIXUTIL_H_
 6 #define GRAPHMATRIXUTIL_H_
 7 
 8 #include <stdlib.h>
 9 #include <stdio.h>
10 #include <limits.h>
11 
12 /*
13  图的邻接矩阵表示
14  */
15 typedef struct    GRAPHMATRIX_STRU
16 {
17     int size;    /* 图中结点的个数 */
18     int **graph;  /*二维数组保存图 */
19 }GraphMatrix;
20 
21 
22 /* 初始化图, 结点的个数num*/
23 GraphMatrix* InitGraph(int num);
24 
25 /* 将数据读入图中 */
26 void ReadGraph(GraphMatrix* graphMatrix);
27 
28 /*将图的结构显示出来*/
29 void WriteGraph(GraphMatrix* graphMatrix);
30 
31 #endif

邻接矩阵，graphmatrixutil.h

 1 /* 
 2     graphmatrixutil.c                                               
 3 */
 4 
 5 #include "graphmatrixutil.h"
 6 
 7 /*初始化图*/
 8 GraphMatrix* InitGraph(int num)
 9 {
10     int i;
11     int j;
12 
13     GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix));    
14     graphMatrix->size = num;/** 图中结点的个数 */
15 
16     /** 给图分配空间 */
17     graphMatrix->graph = (int**)malloc(sizeof(int*) * graphMatrix->size);
18     for (i=0;i<graphMatrix->size;i++)
19     {
20         graphMatrix->graph[i] = (int*)malloc(sizeof(int) * graphMatrix->size);
21     }
22 
23     /** 给图中所有元素设置初值 */
24     for (i=0;i<graphMatrix->size;i++)
25     {
26         for(j=0;j<graphMatrix->size;j++)
27         {
28             graphMatrix->graph[i][j] = INT_MAX;
29         }
30     }
31     return graphMatrix;
32 }
33 
34 /*
35     将数据读入图中
36 */
37 void ReadGraph(GraphMatrix* graphMatrix)
38 {
39     int vex1, vex2, weight;
40 
41     /** 输入方式为点 点 权值，权值为0，则输入结束 */
42     printf("请输入，输入方式为点 点 权值，权值为0，则输入结束\n");
43 
44     scanf("%d%d%d", &vex1, &vex2, &weight);
45     while(weight != 0)
46     {
47         graphMatrix->graph[vex1][vex2] = weight;
48         scanf("%d%d%d", &vex1, &vex2, &weight);
49     }
50 }
51 
52 /*
53     将图的结构显示出来,输出方式为点， 点， 权值
54   */
55 void WriteGraph(GraphMatrix* graphMatrix)
56 {
57     int i, j;
58 
59     printf("图的结构如下，输出方式为点 ，点 ，权值\n");
60     for (i=0;i<graphMatrix->size; i++)
61     {
62         for (j=0; j<graphMatrix->size; j++)
63         {
64             if (graphMatrix->graph[i][j] < INT_MAX)
65             {
66                 printf("%d,%d,%d\n", i, j, graphMatrix->graph[i][j]);
67             }
68         }
69     }
70 }

邻接矩阵，graphmatrixutil.c

 1 /*dijkstrashortdistanc.h
 2 图的最短路径dijkstra算法                                                              
 3 */
 4 #ifndef DIJKSTRASHORTDISTANCE_H_
 5 #define  DIJKSTRASHORTDISTANCE_H_
 6 
 7 #include "graphmatrixutil.h"
 8 
 9 /*
10     dijkstra算法,source起点,graphMatrix图
11  */
12 int*  dijkstra( int source,GraphMatrix *graphMatrix);
13 
14 #endif

dijkstrashortdistanc.h

 1 #include "dijkstrashortdistanc.h"
 2 #include <stdlib.h>
 3 /*
 4     dijkstra算法,source 起点, graphMatrix 图
 5     return distance 最短路径的一维数组
 6 */
 7 
 8 int*  dijkstra( int source,GraphMatrix *graphMatrix)
 9 {
10     int i, j;
11     int vex;
12     int min;
13 
14     int* found = (int *)malloc(sizeof(int) * graphMatrix->size); 
15     int* distance = (int *)malloc(sizeof(int) * graphMatrix->size);
16     for (i = 0; i < graphMatrix->size; i++) 
17     {
18         found[i] = 0;
19         distance[i] = graphMatrix->graph[source][i];
20     }
21     
22     /*将起点加入新点集合中*/
23     found[source] = 1; 
24     distance[source] = 0;
25 
26     for (i = 0; i < graphMatrix->size; i++) 
27     { 
28         min = INT_MAX; /*查找当前距离最小最小的顶点*/
29         for (j = 0; j < graphMatrix->size; j++) 
30         {
31             if (!found[j] && distance[j] < min)
32             {                
33                 vex = j;
34                 min = distance[j];            
35             }
36         }
37         found[vex] = 1;  /*加入到新点集合*/
38 
39         for (j = 0; j < graphMatrix->size; j++) /*新点加入更新距离*/
40         {
41             if (!found[j] && graphMatrix->graph[vex][j] != INT_MAX)
42             { /*若经过新点的距离小,更新距离*/
43                 if (min + graphMatrix->graph[vex][j] < distance[j])
44                 {
45                     distance[j] = min + graphMatrix->graph[vex][j];
46                 }
47             }
48         }
49     }
50     return distance;
51 }

dijkstrashortdistanc.c

 1 #include "dijkstrashortdistance.h"
 2 
 3 
 4 int main()
 5 {
 6     /*最短路径测试*/
 7     GraphMatrix *graphMatrix = NULL;
 8     int *distance = NULL;
 9     int i;
10 
11     graphMatrix = InitGraph(6);
12     ReadGraph(graphMatrix);
13 
14     distance = dijkstra(0, graphMatrix);
15 
16     for (i = 0; i<graphMatrix->size; i++)
17     {
18         if (distance[i]<INT_MAX)
19         {
20             printf("0号结点到%d号结点的最短距离为%d  \n", i,distance[i]);
21         } 
22         else
23         {
24             printf("0号结点到%d号结点无法联通  \n", i);
25         }    
26     }
27 
28     return 0;
29 }

测试文件，main文件

　　代码2　

/* 邻接矩阵存储 - 有权图的单源最短路算法 */
 
Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V;
    int MinDist = INFINITY;
 
    for (V=0; V<Graph->Nv; V++) {
        if ( collected[V]==false && dist[V]<MinDist) {
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else return ERROR;  /* 若这样的顶点不存在，返回错误标记 */
}
 
bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
    int collected[MaxVertexNum];
    Vertex V, W;
 
    /* 初始化：此处默认邻接矩阵中不存在的边用INFINITY表示 */
    for ( V=0; V<Graph->Nv; V++ ) {
        dist[V] = Graph->G[S][V];
        if ( dist[V]<INFINITY )
            path[V] = S;
        else
            path[V] = -1;
        collected[V] = false;
    }
    /* 先将起点收入集合 */
    dist[S] = 0;
    collected[S] = true;
 
    while (1) {
        /* V = 未被收录顶点中dist最小者 */
        V = FindMinDist( Graph, dist, collected );
        if ( V==ERROR ) /* 若这样的V不存在 */
            break;      /* 算法结束 */
        collected[V] = true;  /* 收录V */
        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            /* 若W是V的邻接点并且未被收录 */
            if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {
                if ( Graph->G[V][W]<0 ) /* 若有负边 */
                    return false; /* 不能正确解决，返回错误标记 */
                /* 若收录V使得dist[W]变小 */
                if ( dist[V]+Graph->G[V][W] < dist[W] ) {
                    dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
                    path[W] = V; /* 更新S到W的路径 */
                }
            }
    } /* while结束*/
    return true; /* 算法执行完毕，返回正确标记 */
}

邻接矩阵存储，有权图的单源最短路算法

　　代码3

  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 #include <limits.h>
  4 
  5 #define N 100
  6 int G[N][N];  /* 邻接矩阵图 */
  7 int size = 0;      /* 图的顶点数 */
  8 int* found = NULL;  /*加入到新点集合*/
  9 int *distance = NULL; /* 最短路径长度 */
 10 int* path = NULL;  /* 最短路径 */
 11 
 12 /*
 13     dijkstra算法, source 起点
 14 */
 15 void dijkstra( int source)
 16 {
 17     int i, j;
 18     int vex;
 19     int min;
 20 
 21     found = (int *)malloc(sizeof(int) * size); 
 22     distance = (int *)malloc(sizeof(int) * size);
 23     path = (int*)malloc(sizeof(int) * size);
 24     
 25     for (i = 0; i < size; i++) 
 26     {
 27         found[i] = 0;
 28         /* 从source即顶点0到其他各顶点的距离 */
 29         distance[i] = G[source][i];
 30         /* 与source相通的顶点的前驱顶点是source */
 31         if ( distance[i]<INT_MAX )
 32             path[i] = source;
 33         else
 34             path[i] = -1;
 35     }
 36     
 37     /*将起点加入新点集合中*/
 38     found[source] = 1; 
 39     distance[source] = 0;
 40 
 41     for (i = 0; i < size; i++) 
 42     { 
 43         min = INT_MAX; /*查找当前距离最小的顶点*/
 44         for (j = 0; j < size; j++) 
 45         {
 46             if (!found[j] && distance[j] < min)
 47             {                
 48                 vex = j;
 49                 min = distance[j];            
 50             }
 51         }
 52         if(min==INT_MAX) 
 53             break; /* 如果没找到退出循环 */
 54         found[vex] = 1;  /*加入到新点集合*/
 55         //printf("%d\n", vex);
 56 
 57         for (j = 0; j < size; j++) /*新点加入更新距离*/
 58         {    /* 与新点有边且没有加入新点集合的顶点 */
 59             if (!found[j] && G[vex][j] != INT_MAX)
 60             {  /*若经过新点到顶点source的距离小,更新距离*/
 61                 if (min + G[vex][j] < distance[j])
 62                 {
 63                     distance[j] = min + G[vex][j];
 64                     path[j] = vex;  /* 最短路径前驱顶点 */
 65                 }
 66             }
 67         }
 68     }
 69 }
 70 
 71 void ReadGraph()
 72 {
 73     int i,j;
 74     
 75     /* 初始化图 */    
 76     for (i=0;i<size;i++)
 77     {
 78         for(j=0;j<size;j++)
 79         {
 80             G[i][j] = INT_MAX;
 81         }
 82     }
 83     
 84     /* 读图 */
 85     int vex1, vex2, weight;
 86     printf("请输入，输入方式为点 点 权值，权值为0，则输入结束\n");
 87 
 88     scanf("%d%d%d", &vex1, &vex2, &weight);
 89     while(weight != 0)
 90     {
 91         G[vex1][vex2] = weight;
 92         scanf("%d%d%d", &vex1, &vex2, &weight);
 93     }
 94 }
 95 
 96 void printPath(int v)
 97 {
 98     printf("0号顶点到%d号顶点的最短路径为0", v);
 99     
100     int *stack = (int*)malloc(sizeof(int) * size);
101     int top = -1;
102             
103     for(int j = v; j; j = path[j])
104     {
105         stack[++top] = j;
106     }
107     
108     while(top != -1){
109         printf("->%d",stack[top--]);            
110     }    
111     printf("\n\n");
112     free(stack);
113 }
114 
115 /*最短路径测试*/
116 /* 
117 6
118 0 1 14
119 0 2 20
120 0 4 2
121 1 2 8
122 1 4 5
123 2 3 7
124 4 3 23
125 3 5 3
126 0 0 0 
127 */
128 
129 int main()
130 { 
131     printf("请输入图的顶点数\n");
132     scanf("%d", &size);
133     ReadGraph();  /* 输入图数据 */
134        
135     dijkstra(0);  /* 计算从顶点0到其他顶点的最短路径 */
136     
137     int i,j;    
138     for (i = 1; i< size; i++)
139     {
140         if (distance[i]<INT_MAX) /* 若有最短路径 */
141         {
142             printf("0号顶点到%d号顶点的最短路径长度为%d  \n", i,distance[i]);
143             printPath(i);
144         }          
145     }
146     
147     free(found);
148     free(distance);
149     free(path);
150     
151     return 0;
152 }

Dijkstra，求最短路径及最短路径长度

　　2、多源最短路径问题：求任意两顶点间的最短路径

/* 邻接矩阵存储 - 多源最短路算法 */
 
bool Floyd( MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum] )
{
    Vertex i, j, k;
 
    /* 初始化 */
    for ( i=0; i<Graph->Nv; i++ )
        for( j=0; j<Graph->Nv; j++ ) {
            D[i][j] = Graph->G[i][j];
            path[i][j] = -1;
        }
 
    for( k=0; k<Graph->Nv; k++ )
        for( i=0; i<Graph->Nv; i++ )
            for( j=0; j<Graph->Nv; j++ )
                if( D[i][k] + D[k][j] < D[i][j] ) {
                    D[i][j] = D[i][k] + D[k][j];
                    if ( i==j && D[i][j]<0 ) /* 若发现负值圈 */
                        return false; /* 不能正确解决，返回错误标记 */
                    path[i][j] = k;
                }
    return true; /* 算法执行完毕，返回正确标记 */
}

Floyd 算法

五、最小生成树，是一棵生成树，包含有n个顶点，n-1条边的连通图，无回路，有dfs，bfs生成树，各边权值最小；带权图的最小生成树不唯一；

　　1、Prim最小生成树算法，待选边选短边，采用子树延申法，不需要判回路。

　　（1）、从图中任意顶点Vm开始，将Vm加入到最小生成树；

　　（2）、选择代价最小的边(Vk,Vj)加入到最小生成树中，并将顶点Vj加入到最小生成树，两顶点Vk、Vj属于不同的集合(Vk属于最小生成树)，加入的边不能产生回路；

　　（3）、重复这个过程，直到最小生成树中有n-1条边为止，这时所有顶点也都加入到最小生成树；

　　邻接矩阵存储 - Prim - 1

 1 /** 
 2 * @file graphmatrixutil.h
 3 * @brief 图的邻接矩阵表示以及辅助函数                                                               
 4 */
 5 
 6 #ifndef GRAPHMATRIXUTIL_H_
 7 #define GRAPHMATRIXUTIL_H_
 8 #include <stdlib.h>
 9 #include <stdio.h>
10 #include <limits.h>
11 
12 /**
13  * @brief 图的邻接矩阵表示
14  */
15 typedef struct    GRAPHMATRIX_STRU
16 {
17     int size;/*!< 图中结点的个数 */
18     int **graph;/*!<二维数组保存图 */
19 }GraphMatrix;
20 
21 /**
22   * @brief  初始化图
23   * @param[in]   num    图中结点的个数
24   * @return    用邻接矩阵表示的图
25   */
26 GraphMatrix* InitGraph(int num);
27 
28 /**
29   * @brief  将数据读入图中
30   * @param[in]   graphMatrix    图
31   */
32 void ReadGraph(GraphMatrix* graphMatrix);
33 
34 /**
35   * @brief  将图的结构显示出来
36   * @param[in]   graphMatrix    图
37   */
38 void WriteGraph(GraphMatrix* graphMatrix);
39 
40 #endif

邻接矩阵，graphmatrixutil.h

 1 /** 
 2 * @file graphmatrixutil.cpp
 3 * @brief 图的邻接矩阵表示以及辅助函数                                                               
 4 */
 5 
 6 #include "graphmatrixutil.h"
 7 
 8 /**
 9   * @brief  初始化图
10   * @param[in]   num    图中结点的个数
11   * @return    用邻接矩阵表示的图
12   */
13 GraphMatrix* InitGraph(int num)
14 {
15     int i;
16     int j;
17     GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix));
18     /** 图中结点的个数 */
19     graphMatrix->size = num;
20     /** 给图分配空间 */
21     graphMatrix->graph = (int**)malloc(sizeof(int*) * graphMatrix->size);
22     for (i=0;i<graphMatrix->size;i++)
23     {
24         graphMatrix->graph[i] = (int*)malloc(sizeof(int) * graphMatrix->size);
25     }
26 
27     /** 给图中所有元素设置初值 */
28     for (i=0;i<graphMatrix->size;i++)
29     {
30         for(j=0;j<graphMatrix->size;j++)
31         {
32             graphMatrix->graph[i][j]=INT_MAX;
33         }
34     }
35 
36     return graphMatrix;
37 }
38 
39 /**
40   * @brief  将数据读入图中,方式为点 点  权值，如果输入的权值为0，则输入结束
41   * @param[in]   graphMatrix    图
42   */
43 void ReadGraph(GraphMatrix* graphMatrix)
44 {
45     int vex1, vex2, weight;
46 
47     /** 输入方式为点 点 权值，权值为0，则输入结束 */
48     printf("请输入，输入方式为点 点 权值，权值为0，则输入结束\n");
49     scanf("%d%d%d", &vex1, &vex2, &weight);
50 
51     while(weight != 0)
52     {
53         graphMatrix->graph[vex1][vex2] = weight;
54         scanf("%d%d%d", &vex1, &vex2, &weight);
55     }
56 }
57 
58 /**
59   * @brief  将图的结构显示出来,输出方式为点， 点， 权值
60   * @param[in]   graphMatrix    图
61   */
62 void WriteGraph(GraphMatrix* graphMatrix)
63 {
64     int i, j;
65 
66     printf("图的结构如下，输出方式为点 ，点 ，权值\n");
67     for (i=0;i<graphMatrix->size; i++)
68     {
69         for (j=0; j<graphMatrix->size; j++)
70         {
71             if (graphMatrix->graph[i][j] < INT_MAX)
72             {
73                 printf("%d,%d,%d\n", i, j, graphMatrix->graph[i][j]);
74             }
75         }
76     }
77 }

邻接矩阵，graphmatrixutil.c

 1 /** 
 2 * @file prim.h
 3 * @brief 最小生成树prim算法                                                            
 4 */
 5 
 6 #ifndef PRIM_H_
 7 #define PRIM_H_
 8 
 9 #include "graphmatrixutil.h"
10 
11 /**
12   * @brief  prim算法
13   * @param[in]   source    起点
14   * @param[in]   graphMatrix    图
15   * @return    最小生成树
16   */
17 GraphMatrix*  prim( int source,GraphMatrix *graphMatrix);
18 
19 #endif

最小生成树，Prim.h

 1 #include "prim.h"
 2 
 3 GraphMatrix*  prim( int source,GraphMatrix *graphMatrix)
 4 {
 5     int i,j,min,v,*component,*distance,*neighbor;
 6     GraphMatrix* tree;
 7     /*生成树顶点集合*/
 8     component = (int*)malloc(sizeof(graphMatrix->size));
 9     /*两顶点之间距离*/
10     distance = (int*)malloc(sizeof(graphMatrix->size));
11     /*顶点邻边,如neighbor[i]=j表示i的邻居是j*/
12     neighbor = (int*)malloc(sizeof(graphMatrix->size));
13 
14     /*初始化*/
15     for (i=0; i<graphMatrix->size; i++)
16     {
17         component[i] = 0;
18         distance[i] = graphMatrix->graph[source][i];
19         neighbor[i] = source;
20     }    
21     component[source] = 1;/*起点放到生成树集合*/
22 
23     /*最小生成树*/
24     tree = InitGraph(graphMatrix->size);
25     /*生成树每次加入一个顶点*/
26     for (i=1; i<graphMatrix->size; i++)
27     {
28         min = INT_MAX;  /*最小值*/
29         
30         for (j=0; j<graphMatrix->size; j++)
31         {
32             if(!component[j])/*非最小生成树的顶点找最小边*/
33             {
34                 if (distance[j] < min)
35                 {
36                     v = j;
37                     min = distance[j];
38                 }
39             }
40         }
41 
42         if (min < INT_MAX) /*找到最小边, 更新*/
43         {
44             component[v] = 1;
45             tree->graph[v][neighbor[v]] = distance[v];
46             tree->graph[neighbor[v]][v] = distance[v];
47 
48             for (j=0; j<graphMatrix->size; j++)
49             {
50                 if (!component[j])
51                 {
52                     if (graphMatrix->graph[v][j]<distance[j])
53                     {
54                         distance[j] = graphMatrix->graph[v][j];
55                         neighbor[j] = v;
56                     }
57                 }
58             }
59         }
60         else
61         {
62             break;
63         }
64     }
65     return tree;
66 }

最小生成树，Prim.c

 1 #include "prim.h"
 2 
 3 int main()
 4 {
 5     /*最小生成树测试*/
 6     GraphMatrix *graphMatrix = NULL;
 7     GraphMatrix *tree = NULL;
 8     graphMatrix = InitGraph(6);
 9 
10     ReadGraph(graphMatrix);
11     tree = prim(0, graphMatrix);
12     WriteGraph(tree);
13 
14     return 0;
15 }

测试文件，main文件

　　邻接矩阵存储 - Prim - 2

/* 邻接矩阵存储 - Prim最小生成树算法 */
 
Vertex FindMinDist( MGraph Graph, WeightType dist[] )
{ /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V;
    WeightType MinDist = INFINITY;
 
    for (V=0; V<Graph->Nv; V++) {
        if ( dist[V]!=0 && dist[V]<MinDist) {
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else return ERROR;  /* 若这样的顶点不存在，返回-1作为标记 */
}
 
int Prim( MGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
    WeightType dist[MaxVertexNum], TotalWeight;
    Vertex parent[MaxVertexNum], V, W;
    int VCount;
    Edge E;
     
    /* 初始化。默认初始点下标是0 */
       for (V=0; V<Graph->Nv; V++) {
        /* 这里假设若V到W没有直接的边，则Graph->G[V][W]定义为INFINITY */
           dist[V] = Graph->G[0][V];
           parent[V] = 0; /* 暂且定义所有顶点的父结点都是初始点0 */ 
    }
    TotalWeight = 0; /* 初始化权重和     */
    VCount = 0;      /* 初始化收录的顶点数 */
    /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
    MST = CreateGraph(Graph->Nv);
    E = (Edge)malloc( sizeof(struct ENode) ); /* 建立空的边结点 */
            
    /* 将初始点0收录进MST */
    dist[0] = 0;
    VCount ++;
    parent[0] = -1; /* 当前树根是0 */
 
    while (1) {
        V = FindMinDist( Graph, dist );
        /* V = 未被收录顶点中dist最小者 */
        if ( V==ERROR ) /* 若这样的V不存在 */
            break;   /* 算法结束 */
             
        /* 将V及相应的边<parent[V], V>收录进MST */
        E->V1 = parent[V];
        E->V2 = V;
        E->Weight = dist[V];
        InsertEdge( MST, E );
        TotalWeight += dist[V];
        dist[V] = 0;
        VCount++;
         
        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            if ( dist[W]!=0 && Graph->G[V][W]<INFINITY ) {
            /* 若W是V的邻接点并且未被收录 */
                if ( Graph->G[V][W] < dist[W] ) {
                /* 若收录V使得dist[W]变小 */
                    dist[W] = Graph->G[V][W]; /* 更新dist[W] */
                    parent[W] = V; /* 更新树 */
                }
            }
    } /* while结束*/
    if ( VCount < Graph->Nv ) /* MST中收的顶点不到|V|个 */
       TotalWeight = ERROR;
    return TotalWeight;   /* 算法执行完毕，返回最小权重和或错误标记 */
}

邻接矩阵存储

　　2、Kruskal最小生成树算法，全图选短边，采用子树合并法，需要判回路，由一棵空树，从小到大，添加n-1条边，添加边的过程中，形成回路的边舍弃；第一，边的个数为n-1条；第二，E中选取最短边++；第三，形成回路的边舍弃；

　　邻接矩阵存储 - Kruskal，通过判断是否是同一连通分量，来确定是否形成回路，用一个数组记录顶点所属的连通分量

 1 /* 
 2     graphmatrixutil.h                                                       
 3 */
 4 
 5 #ifndef GRAPHMATRIXUTIL_H_
 6 #define GRAPHMATRIXUTIL_H_
 7 
 8 #include <stdlib.h>
 9 #include <stdio.h>
10 #include <limits.h>
11 
12 /*
13  图的邻接矩阵表示
14  */
15 typedef struct    GRAPHMATRIX_STRU
16 {
17     int size;    /* 图中结点的个数 */
18     int **graph;  /*二维数组保存图 */
19 }GraphMatrix;
20 
21 
22 /* 初始化图, 结点的个数num*/
23 GraphMatrix* InitGraph(int num);
24 
25 /* 将数据读入图中 */
26 void ReadGraph(GraphMatrix* graphMatrix);
27 
28 /*将图的结构显示出来*/
29 void WriteGraph(GraphMatrix* graphMatrix);
30 
31 #endif

邻接矩阵，graphmatrixutil.h

 1 /* 
 2     graphmatrixutil.c                                               
 3 */
 4 
 5 #include "graphmatrixutil.h"
 6 
 7 /*初始化图*/
 8 GraphMatrix* InitGraph(int num)
 9 {
10     int i;
11     int j;
12 
13     GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix))    
14     graphMatrix->size = num;/** 图中结点的个数 */
15 
16     /** 给图分配空间 */
17     graphMatrix->graph = (int**)malloc(sizeof(int*) * graphMatrix->size);
18     for (i=0;i<graphMatrix->size;i++)
19     {
20         graphMatrix->graph[i] = (int*)malloc(sizeof(int) * graphMatrix->size);
21     }
22 
23     /** 给图中所有元素设置初值 */
24     for (i=0;i<graphMatrix->size;i++)
25     {
26         for(j=0;j<graphMatrix->size;j++)
27         {
28             graphMatrix->graph[i][j] = INT_MAX;
29         }
30     }
31     return graphMatrix;
32 }
33 
34 /*
35     将数据读入图中
36 */
37 void ReadGraph(GraphMatrix* graphMatrix)
38 {
39     int vex1, vex2, weight;
40 
41     /** 输入方式为点 点 权值，权值为0，则输入结束 */
42     printf("请输入，输入方式为点 点 权值，权值为0，则输入结束\n");
43 
44     scanf("%d%d%d", &vex1, &vex2, &weight);
45     while(weight != 0)
46     {
47         graphMatrix->graph[vex1][vex2] = weight;
48         scanf("%d%d%d", &vex1, &vex2, &weight);
49     }
50 }
51 
52 /*
53     将图的结构显示出来,输出方式为点， 点， 权值
54   */
55 void WriteGraph(GraphMatrix* graphMatrix)
56 {
57     int i, j;
58 
59     printf("图的结构如下，输出方式为点 ，点 ，权值\n");
60     for (i=0;i<graphMatrix->size; i++)
61     {
62         for (j=0; j<graphMatrix->size; j++)
63         {
64             if (graphMatrix->graph[i][j] < INT_MAX)
65             {
66                 printf("%d,%d,%d\n", i, j, graphMatrix->graph[i][j]);
67             }
68         }
69     }
70 }

邻接矩阵，graphmatrixutil.c

 1 #ifndef KRUSKAL_H_
 2 #define KRUSKAL_H_
 3 #include "graphmatrixutil.h"
 4 
 5 /*
 6   边的结构
 7  */
 8 typedef struct    EDGE_STRU
 9 {
10     int begin;  /*  起点 */
11     int end;    /* 终点 */
12     int weight; /* 权值 */
13 }Edge;
14 
15 /* 最小生成树, kruskal算法*/
16 GraphMatrix*  kruskal( GraphMatrix *graphMatrix);
17 
18 #endif

最小生成树，Kruskal.h

 1 /*
 2     kruskal算法, 最小生成树, kruskal.c
 3     图, graphMatrix
 4 */
 5 
 6 #include "kruskal.h"
 7 
 8 GraphMatrix*  kruskal( GraphMatrix *graphMatrix)
 9 {
10     int i,j,k;
11 
12     int edgeNum = 0;  /*边数*/
13     Edge *edge = NULL; /*边集合*/
14     Edge tempEdge;  /*给边排序时候的临时变量*/    
15 
16     int *group;    /*记录点是否属于同一连通分量*/
17     int changeGroup;  /*记录要变化的连通值*/
18     
19     /*最小生成树图*/
20     GraphMatrix* tree = InitGraph(graphMatrix->size);
21 
22     /*避免回路的连通集合*/
23     group = (int*)malloc(sizeof(int)*graphMatrix->size);
24     for (i=0;i<graphMatrix->size;i++)
25     {
26         group[i] = i; /*初始顶点没有连通*/
27      }
28 
29     /*********边的大小排序***开始***********/
30     /*分析有多少条边*/
31     for (i=0; i<graphMatrix->size; i++)
32     {
33         for (j=i+1; j<graphMatrix->size; j++)
34         {
35             if (graphMatrix->graph[i][j] < INT_MAX)
36             {
37                 edgeNum++;
38             }
39         }
40     }
41     edge = (Edge*)malloc(sizeof(Edge)*edgeNum); /*边集空间*/
42     k = 0; /*边下标初值*/
43     for (i=0; i<graphMatrix->size; i++)
44     {
45         for (j=i+1; j<graphMatrix->size; j++)
46         {
47             if (graphMatrix->graph[i][j] < INT_MAX)
48             {
49                 edge[k].begin = i;
50                 edge[k].end = j;
51                 edge[k].weight = graphMatrix->graph[i][j] ;                
52                 k++;
53             }
54         }
55     }
56     /*边冒泡排序*/
57     for (i=0;i<edgeNum;i++)
58     {
59         for (j=i+1;j<edgeNum;j++)
60         {
61             if (edge[i].weight > edge[j].weight)
62             {
63                 tempEdge = edge[i];
64                 edge[i] = edge[j];
65                 edge[j] = tempEdge;
66             }
67         }
68     }
69     /*********边的大小排序***结束***********/
70 
71     /*从排好序的边集中, 从小到大加入边*/
72     for (i=0;i<edgeNum;i++)
73     {    
74         /*只添加终点和起点属于两个不同连通分量的边, 防止形成回路*/ 
75         if (group[edge[i].begin] != group[edge[i].end])
76         {
77             /*添加到树中*/
78             tree->graph[edge[i].begin][edge[i].end] = edge[i].weight;
79             tree->graph[edge[i].end][edge[i].begin] = edge[i].weight;
80             /*更新所有跟终点属于同一连通分量的点的连通值*/
81             changeGroup = group[edge[i].end];
82             for (j=0;j<edgeNum;j++)
83             {
84                 if (group[j] == changeGroup)
85                 {
86                     group[j] = group[edge[i].begin];
87                 }
88             }
89         }
90     }
91     return tree;
92 }

最小生成树，Kruskal.c

 1 /*
 2 0 1 5
 3 1 0 5
 4 0 2 30
 5 2 0 30
 6 0 3 14
 7 3 0 14
 8 1 2 24
 9 2 1 24
10 2 3 17
11 3 2 17
12 1 4 14
13 4 1 14
14 1 5 10
15 5 1 10
16 4 5 25
17 5 4 25
18 2 5 17
19 5 2 17
20 3 5 8
21 5 3 8
22 0 0 0
23 */
24 #include "kruskal.h"
25 
26 int main()
27 {
28     GraphMatrix *graphMatrix = NULL;
29     GraphMatrix *tree = NULL;
30     graphMatrix = InitGraph(6);
31 
32     ReadGraph(graphMatrix);
33     tree = kruskal(graphMatrix);
34     WriteGraph(tree);
35 
36     return 0;
37 }

测试文件，main文件

　　邻接表存储 - Kruskal

/* 邻接表存储 - Kruskal最小生成树算法 */
 
/*-------------------- 顶点并查集定义 --------------------*/
typedef Vertex ElementType; /* 默认元素可以用非负整数表示 */
typedef Vertex SetName;     /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */
 
void InitializeVSet( SetType S, int N )
{ /* 初始化并查集 */
    ElementType X;
 
    for ( X=0; X<N; X++ ) S[X] = -1;
}
 
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
    /* 保证小集合并入大集合 */
    if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
        S[Root2] += S[Root1];     /* 集合1并入集合2  */
        S[Root1] = Root2;
    }
    else {                         /* 如果集合1比较大 */
        S[Root1] += S[Root2];     /* 集合2并入集合1  */
        S[Root2] = Root1;
    }
}
 
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
    if ( S[X] < 0 ) /* 找到集合的根 */
        return X;
    else
        return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
 
bool CheckCycle( SetType VSet, Vertex V1, Vertex V2 )
{ /* 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路 */
    Vertex Root1, Root2;
 
    Root1 = Find( VSet, V1 ); /* 得到V1所属的连通集名称 */
    Root2 = Find( VSet, V2 ); /* 得到V2所属的连通集名称 */
 
    if( Root1==Root2 ) /* 若V1和V2已经连通，则该边不能要 */
        return false;
    else { /* 否则该边可以被收集，同时将V1和V2并入同一连通集 */
        Union( VSet, Root1, Root2 );
        return true;
    }
}
/*-------------------- 并查集定义结束 --------------------*/
 
/*-------------------- 边的最小堆定义 --------------------*/
void PercDown( Edge ESet, int p, int N )
{ /* 改编代码4.24的PercDown( MaxHeap H, int p )    */
  /* 将N个元素的边数组中以ESet[p]为根的子堆调整为关于Weight的最小堆 */
    int Parent, Child;
    struct ENode X;
 
    X = ESet[p]; /* 取出根结点存放的值 */
    for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
        Child = Parent * 2 + 1;
        if( (Child!=N-1) && (ESet[Child].Weight>ESet[Child+1].Weight) )
            Child++;  /* Child指向左右子结点的较小者 */
        if( X.Weight <= ESet[Child].Weight ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            ESet[Parent] = ESet[Child];
    }
    ESet[Parent] = X;
}
 
void InitializeESet( LGraph Graph, Edge ESet )
{ /* 将图的边存入数组ESet，并且初始化为最小堆 */
    Vertex V;
    PtrToAdjVNode W;
    int ECount;
 
    /* 将图的边存入数组ESet */
    ECount = 0;
    for ( V=0; V<Graph->Nv; V++ )
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
            if ( V < W->AdjV ) { /* 避免重复录入无向图的边，只收V1<V2的边 */
                ESet[ECount].V1 = V;
                ESet[ECount].V2 = W->AdjV;
                ESet[ECount++].Weight = W->Weight;
            }
    /* 初始化为最小堆 */
    for ( ECount=Graph->Ne/2; ECount>=0; ECount-- )
        PercDown( ESet, ECount, Graph->Ne );
}
 
int GetEdge( Edge ESet, int CurrentSize )
{ /* 给定当前堆的大小CurrentSize，将当前最小边位置弹出并调整堆 */
 
    /* 将最小边与当前堆的最后一个位置的边交换 */
    Swap( &ESet[0], &ESet[CurrentSize-1]);
    /* 将剩下的边继续调整成最小堆 */
    PercDown( ESet, 0, CurrentSize-1 );
 
    return CurrentSize-1; /* 返回最小边所在位置 */
}
/*-------------------- 最小堆定义结束 --------------------*/
 
 
int Kruskal( LGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
    WeightType TotalWeight;
    int ECount, NextEdge;
    SetType VSet; /* 顶点数组 */
    Edge ESet;    /* 边数组 */
 
    InitializeVSet( VSet, Graph->Nv ); /* 初始化顶点并查集 */
    ESet = (Edge)malloc( sizeof(struct ENode)*Graph->Ne );
    InitializeESet( Graph, ESet ); /* 初始化边的最小堆 */
    /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
    MST = CreateGraph(Graph->Nv);
    TotalWeight = 0; /* 初始化权重和     */
    ECount = 0;      /* 初始化收录的边数 */
 
    NextEdge = Graph->Ne; /* 原始边集的规模 */
    while ( ECount < Graph->Nv-1 ) {  /* 当收集的边不足以构成树时 */
        NextEdge = GetEdge( ESet, NextEdge ); /* 从边集中得到最小边的位置 */
        if (NextEdge < 0) /* 边集已空 */
            break;
        /* 如果该边的加入不构成回路，即两端结点不属于同一连通集 */
        if ( CheckCycle( VSet, ESet[NextEdge].V1, ESet[NextEdge].V2 )==true ) {
            /* 将该边插入MST */
            InsertEdge( MST, ESet+NextEdge );
            TotalWeight += ESet[NextEdge].Weight; /* 累计权重 */
            ECount++; /* 生成树中边数加1 */
        }
    }
    if ( ECount < Graph->Nv-1 )
        TotalWeight = -1; /* 设置错误标记，表示生成树不存在 */
 
    return TotalWeight;
}

邻接表存储

六、拓扑排序，AOV网，顶点活动网，Activity On Vertex network,有向图，无环，顶点表示活动，边表示活动的先后依赖关系；从AOV网中选择一个入度为0的顶点将其输出；在AOV网中删除此顶点及其所有的出边；重复执行以上两步，直到所有顶点都已经输出为止，形成一个拓扑序列；一个AOV网的拓扑序列不是唯一的；AOV网如果有回路一定不能完成拓扑排序；

　　拓扑排序算法过程
　　(1)、计算各个顶点的入度；
　　(2)、将入度为0的顶点入栈；
　　(3)、如果栈不空，从栈中取出一个元素v，输出到拓扑序列中；
　　(4)、检查顶点v的出边表，将出边表中的每个顶点w的入度减1(即删除顶点v为弧头的边表)，如果w的入度为0，则顶点w入栈；
　　(5)、重复第3、4，直到栈为空结束

　　代码1

 1 #ifndef LINKSTACK_H_
 2 #define LINKSTACK_H_
 3 
 4 #define FALSE 0
 5 #define TRUE 1
 6 
 7 typedef int DataType;
 8 struct Node{
 9     DataType      data;
10     struct Node*  next;
11 };
12 typedef struct Node  *PNode;
13 typedef struct Node  *top,*LinkStack;
14 
15 LinkStack SetNullStack_Link();
16 int IsNullStack_link(LinkStack top);
17 void Push_link(LinkStack top, DataType x);
18 void Pop_link(LinkStack top);
19 DataType Pop_seq_return(LinkStack top);
20 DataType Top_link(LinkStack top);
21 #endif

链栈, linkstack.h

 1 #include<stdio.h>
 2 #include<stdlib.h>
 3 #include "linkstack.h"
 4 
 5 LinkStack SetNullStack_Link() /*创建带有头结点的空链栈*/
 6 {
 7     LinkStack top = (LinkStack)malloc(sizeof(struct Node));
 8     if (top!= NULL) top->next = NULL;
 9     else printf("Alloc failure");
10     return top; /*返回栈顶指针*/
11 }
12 
13 int IsNullStack_link(LinkStack top) /*判断一个链栈是否为空*/
14 {
15     if (top->next == NULL)
16         return 1;
17     else
18         return 0;
19 }
20 
21 void Push_link(LinkStack top, DataType x) /*进栈*/
22 {
23     PNode p;
24     p = (PNode)malloc(sizeof(struct Node));
25     if (p == NULL)
26         printf("Alloc failure");
27     else
28     {
29         p->data = x;
30         p->next = top->next;
31         top->next = p;
32     }
33 } 
34 
35 void Pop_link(LinkStack top) /*删除栈顶元素*/
36 {
37     PNode p;
38     if (top->next == NULL) 
39         printf("it is empty stack!");
40     else
41     {
42         p = top->next;
43         top->next = p->next;
44         free(p);
45     }
46 }
47 
48 DataType Pop_seq_return(LinkStack top) /*删除栈顶元素*/
49 {
50     PNode p; DataType temp;
51     if (top->next == NULL)
52     {
53         printf("It is empty stack!");
54         return 0;
55     }
56     else
57     {
58         p = top->next;
59         top->next = p->next;
60         temp = p->data;
61         free(p);
62         return temp;
63     }
64 }
65 
66 DataType Top_link(LinkStack top) /*求栈顶元素的值*/
67 {
68     if (top->next == NULL)
69     {
70         printf("It is empty stack!");
71         return 0;
72     }
73     else
74         return top->next->data;
75 }

链栈, linkstack.c

 1 /* 
 2     图的邻接表表示及辅助函数 
 3     graphlistutil.h
 4 */
 5 #ifndef GRAPHLISTUTIL_H_
 6 #define GRAPHLISTUTIL_H_
 7 
 8 /* 图结点结构体 */
 9 typedef struct GRAPHLISTNODE_STRU{
10     int nodeno; /* 结点的编号 */
11     struct GRAPHLISTNODE_STRU* next;
12 }GraphListNode;
13 
14 /* 图结构体 */
15 typedef struct GRAPHLIST_STRU{
16     int size;     /* 图中结点的个数 */
17     GraphListNode* graphListArray;   /* 图的邻接表 */
18 }GraphList;     /* 定义结构体类型 */
19 
20 /* 初始化图 */
21 GraphList* InitGraph(int num);
22 
23 /* 将数据读入图 */
24 void ReadGraph(GraphList* graphList);
25 
26 /* 将图的结构显示出来 */
27 void WriteGraph(GraphList* graphList);
28 
29 #endif

邻接表，graphlistutil.h

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #include "graphListutil.h"
 4 
 5 /* 初始化图，num表示图中结点个数，邻接表表示图 */
 6 GraphList* InitGraph(int num)
 7 {
 8     int i;
 9     /* 图空间定义 */
10     GraphList* graphList = (GraphList*)malloc(sizeof(GraphList));    
11     graphList->size = num;/* 图中结点数 */
12     
13     /* 邻接表数组分配空间 */
14     graphList->graphListArray = (GraphListNode*)malloc(sizeof(GraphListNode)*graphList->size); 
15     /* 邻接表数组赋值 */
16     for(i=0; i<graphList->size; ++i){
17         graphList->graphListArray[i].next = NULL;
18         graphList->graphListArray[i].nodeno = i;
19     }
20     return graphList;  /* 返回图结构体指针 */
21 }
22 
23 /* 读入图中顶点 */
24 void ReadGraph(GraphList* graphList)
25 {
26     int vex1,vex2;
27     GraphListNode* tempNodePtr = NULL;
28     printf("请输入顶点，顶点，顶点为-1，则输入结束\n");
29     scanf("%d%d", &vex1, &vex2);
30     while(vex1>=0 && vex2>=0)
31     {
32         tempNodePtr = (GraphList*)malloc(sizeof(GraphListNode));
33         tempNodePtr->nodeno = vex2;
34         tempNodePtr->next = NULL;
35         tempNodePtr->next = graphList->graphListArray[vex1].next;
36         graphList->graphListArray[vex1].next = tempNodePtr;
37         scanf("%d%d", &vex1, &vex2);
38     }
39 }
40 
41 /* 输出图中顶点  */
42 void WriteGraph(GraphList* graphList)
43 {
44     int i;
45     GraphListNode* tempNodePtr = NULL;
46     printf("图的结构如下，输出方式为顶点，顶点\n");
47     for(i=0; i<graphList->size; ++i){
48         tempNodePtr = graphList->graphListArray[i].next;
49         while(tempNodePtr){           
50             printf("结点%d到结点%d有边相连\n",i,tempNodePtr->nodeno);         
51             tempNodePtr = tempNodePtr->next;
52         }
53     }
54 }

邻接表，graphlistutil.c

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #include "linkstack.h"
 4 #include "graphlistutil.h"
 5 
 6 /*拓扑排序,graphList邻接表表示的图*/
 7 int topologicalsort(GraphList *graphList)
 8 {
 9     int i;
10     int cnt;  /*记录顶点数*/
11     int nodeNum;
12     int success = 1;
13 
14     LinkStack nodeStack = NULL;
15     GraphListNode *tempNode = NULL;
16     int *inPoint = (int *)malloc(sizeof(int) * graphList->size);
17 
18     nodeStack = SetNullStack_Link();    
19     for (i=0; i<graphList->size; i++)
20     {
21         inPoint[i] = 0;
22     }
23 
24     /*计算入度*/
25     for (i=0; i<graphList->size; i++)
26     {
27         tempNode = graphList->graphListArray[i].next;
28         
29         while(tempNode != NULL)
30         {
31             inPoint[tempNode->nodeno]++;
32             tempNode = tempNode->next;
33         }
34     }
35 
36     /*度为0的顶点入栈*/
37     for(i=0; i<graphList->size; i++)
38     {
39         if (inPoint[i] == 0)
40         {
41             Push_link(nodeStack, i);
42         }
43     }
44 
45     cnt = 0; /*记录顶点数*/
46     while(!IsNullStack_link(nodeStack))
47     { /*取栈顶元素*/
48         nodeNum = Top_link(nodeStack);
49         printf("%d ", nodeNum);
50         Pop_link(nodeStack);
51         cnt++;
52 
53         /*将每条出边的终端顶点的入度减1,若该顶点入度为0入栈*/
54         tempNode = graphList->graphListArray[nodeNum].next;
55         while(tempNode != NULL)
56         {
57             inPoint[tempNode->nodeno]--;  /*入度--*/
58             if (inPoint[tempNode->nodeno] == 0) /*度为0入栈*/
59             {
60                 Push_link(nodeStack, tempNode->nodeno);
61             }
62             tempNode = tempNode->next;
63         }
64     }
65 
66     /*栈空,还有顶点,有回路,无法完成拓扑排序*/
67     if (cnt != graphList->size)
68     {
69         success = 0;
70     } 
71 
72     return success;
73 }
74 
75 int main()
76 {
77     GraphList *graphList = InitGraph(8);
78     int result = 0;
79 
80     ReadGraph(graphList);
81     WriteGraph(graphList);
82 
83     result = topologicalsort(graphList);
84     if (result == 1)
85     {
86         printf("拓扑排序成功\n");
87     } 
88     else
89     {
90         printf("拓扑排序失败\n");
91     }
92 
93     return 0;
94 }

拓扑排序

　　代码2 队列存储入度为0的顶点

/* 邻接表存储 - 拓扑排序算法 */
 
bool TopSort( LGraph Graph, Vertex TopOrder[] )
{ /* 对Graph进行拓扑排序,  TopOrder[]顺序存储排序后的顶点下标 */
    int Indegree[MaxVertexNum], cnt;
    Vertex V;
    PtrToAdjVNode W;
       Queue Q = CreateQueue( Graph->Nv );
  
    /* 初始化Indegree[] */
    for (V=0; V<Graph->Nv; V++)
        Indegree[V] = 0;
         
    /* 遍历图，得到Indegree[] */
    for (V=0; V<Graph->Nv; V++)
        for (W=Graph->G[V].FirstEdge; W; W=W->Next)
            Indegree[W->AdjV]++; /* 对有向边<V, W->AdjV>累计终点的入度 */
             
    /* 将所有入度为0的顶点入列 */
    for (V=0; V<Graph->Nv; V++)
        if ( Indegree[V]==0 )
            AddQ(Q, V);
             
    /* 下面进入拓扑排序 */ 
    cnt = 0; 
    while( !IsEmpty(Q) ){
        V = DeleteQ(Q); /* 弹出一个入度为0的顶点 */
        TopOrder[cnt++] = V; /* 将之存为结果序列的下一个元素 */
        /* 对V的每个邻接点W->AdjV */
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
            if ( --Indegree[W->AdjV] == 0 )/* 若删除V使得W->AdjV入度为0 */
                AddQ(Q, W->AdjV); /* 则该顶点入列 */ 
    } /* while结束*/
     
    if ( cnt != Graph->Nv )
        return false; /* 说明图中有回路, 返回不成功标志 */ 
    else
        return true;
}

邻接表存储

　　代码3 栈存储入度为0的顶点

int TopoSort (AdjList G)
{
    Stack S;
    int indegree[MAX_VERTEX_NUM];
    int i, count, k;
    ArcNode *p;
    
    FindID(G,indegree); /*求各顶点入度*/
    InitStack(&S);
    
    for(i=0;i<G.vexnum;i++)
        if( indegree[i]==0 ) Push(&S,i);  /* 1.入度为0的顶点入栈 */
            
    count=0;
    
    while(!StackEmpty(S))
    {
        Pop(&S,&i);
        printf("%c",G.vertex[i].data);
        count++;

        p=G.vertexes[i].firstarc;
        while(p != NULL) /* 2.邻接点 */
        { 
            k=p->adjvex;
            indegree[k]--;
            if(indegree[k]==0)  Push(&S, k);
            p = p->next ;   /* 3. */
        }
    } /*while*/

    if (count < G.vexnum)  
        return(Error);
    else  
        return(Ok);
}

邻接表存储

七、关键路径，AOE网，Activity On Edge worknet，带权的有向图；顶点表示事件，有向边表示活动；边上的权值表示活动持续的时间；顶点所表示的事件实际上就是它的入边所表示活动都已完成，它的出边所表示的活动可以开始这样一种状态；只有一个入度为0的顶点，表示开始，只有一个出度为0的顶点，表示结束；从开始顶点到完成顶点的最长路径称为关键路径，并不一定是唯一；事件的最早的发生时间要大于最迟发生时间

　　事件的最早发生时间，事件Vi的最早可能的开始事件（从顶点开始，正向），是从开始顶点V0到顶点Vi的最长路径的长度，计算事件的最早发生时间，采用正向递推的方式，初始earliesTime[0] = 0; earliestTime[j] = max{ earliestTime[i] + weight<vi,vj> }，<vi,vj> 是以vj为终点的所有有向边 ；

　　事件的最迟发生时间，latestTime，事件Vi最迟允许的开始时间（从汇点开始，反向），是指在不推迟整个工期的前提下（即在保证汇点按其最早发生时间发生这一前提下），事件Vi允许的最晚时间，采用反向递推的方式，初始latesTime[n-1] = earliestTime[n-1]; latestTime[j] = min{ latestTime[i] - weight<vj,vi> }， <vj,vi> 是以vj为起点的所有有向边；

　　活动的最早发生时间，activityEarliestTime，设ck是边<vi,vj>上的活动，则activityEarliestTime是源点v0到起始顶点vi的最长路径长度，即为，activityEarliestTime[k] = earliestTime[i]；

　　活动的最迟发生时间，activityLatestTime，设ck是边<vi,vj>上的活动，则activityLatestTime是在不引起时间延误的前提下，活动ck允许的最迟时间，也就是顶点时间vj的最迟发生时间减去活动ck持续的时间weight<vi,vj>，即为，activityLatestTime[k] = latestTime[j] - weight<vi,vj>；

　　活动的时间余量，reminder，reminder[k]表示活动ck的最早发生时间和最迟发生时间的时间余量，即为，reminder[k] = activityLatestTime[k] - activityEarliestTime[k]，当activityLatestTime[k] == activityEarliestTime[k]时，reminder[k]==0，表示该活动ck的时间余量为0，即该活动为关键活动；

 1 typedef int DataType;
 2 struct Node{
 3     DataType      data;
 4     struct Node*  next;
 5 };
 6 typedef struct Node  *PNode;
 7 typedef struct Node  *top,*LinkStack;
 8 
 9 LinkStack SetNullStack_Link();
10 int IsNullStack_link(LinkStack top);
11 void Push_link(LinkStack top, DataType x);
12 void Pop_link(LinkStack top);
13 DataType Pop_seq_return(LinkStack top);
14 DataType Top_link(LinkStack top);
15 #endif

链栈, linkstack.h

 1 #include<stdio.h>
 2 #include<stdlib.h>
 3 #include "linkstack.h"
 4 
 5 LinkStack SetNullStack_Link() /*创建带有头结点的空链栈*/
 6 {
 7     LinkStack top = (LinkStack)malloc(sizeof(struct Node));
 8     if (top!= NULL) top->next = NULL;
 9     else printf("Alloc failure");
10     return top; /*返回栈顶指针*/
11 }
12 
13 int IsNullStack_link(LinkStack top)/*判断一个链栈是否为空*/
14 {
15     if (top->next == NULL)
16         return 1;
17     else
18         return 0;
19 }
20 
21 void Push_link(LinkStack top, DataType x) /*进栈*/
22 {
23     PNode p;
24     p = (PNode)malloc(sizeof(struct Node));
25     if (p == NULL)
26         printf("Alloc failure");
27     else
28     {
29         p->data = x;
30         p->next = top->next;
31         top->next = p;
32     }
33 }
34 
35 void Pop_link(LinkStack top) /*删除栈顶元素*/
36 {
37     PNode p;
38     if (top->next == NULL) 
39         printf("it is empty stack!");
40     else
41     {
42         p = top->next;
43         top->next = p->next;
44         free(p);
45     }
46 }
47 
48 DataType Pop_seq_return(LinkStack top) /*删除栈顶元素*/
49 {
50     PNode p; DataType temp;
51     if (top->next == NULL)
52     {
53         printf("It is empty stack!");
54         return 0;
55     }
56     else
57     {
58         p = top->next;
59         top->next = p->next;
60         temp = p->data;
61         free(p);
62         return temp;
63     }
64 }
65 
66 DataType Top_link(LinkStack top) /*求栈顶元素的值*/
67 {
68     if (top->next == NULL)
69     {
70         printf("It is empty stack!");
71         return 0;
72     }
73     else
74         return top->next->data;
75 }

链栈, linkstack.c

 1 /*
 2     graphlistutil.h
 3     图的邻接表表示及函数                                                               
 4 */
 5 #ifndef GRAPHLISTUTIL_H
 6 #define GRAPHLISTUTIL_H
 7 
 8 typedef struct    GRAPHLISTNODE_STRU
 9 {
10     int nodeno; /*  图中结点的编号 */
11     int weight;/*   图中边的权值 */
12     struct    GRAPHLISTNODE_STRU* next;/* 指向下一个结点的指针 */
13 }GraphListNode;
14 
15 typedef struct    GRAPHLIST_STRU
16 {
17     int size;/* 图中结点的个数 */
18     GraphListNode* graphListArray;/* 图的邻接表 */
19 }GraphList;
20 
21 /* 初始化图,num 图中结点的个数
22   */
23 GraphList* InitGraph(int num);
24 
25 /* 将数据读入图中
26   */
27 void ReadGraph(GraphList* graphList);
28 
29 /*将图的结构显示出来
30   */
31 void WriteGraph(GraphList* graphList);
32 
33 #endif

邻接表，graphlistutil.h

 1 #include "graphlistutil.h"
 2 #include <stdlib.h>
 3 #include <stdio.h>
 4 
 5 /* 初始化图，num表示图中结点个数，邻接表表示图 */
 6 GraphList* InitGraph(int num)
 7 {
 8     int i;
 9     GraphList *graphList = (GraphList *)malloc(sizeof(GraphList));
10     
11     graphList->size = num;
12     graphList->graphListArray = (GraphListNode*)malloc(sizeof(GraphListNode)*num);
13     
14     for (i=0; i<num; i++)
15     {
16         graphList->graphListArray[i].next = NULL;
17         graphList->graphListArray[i].nodeno = i;
18     }
19     
20     return graphList;
21 }
22 
23 /* 读入图中顶点 */
24 void ReadGraph(GraphList* graphList)
25 {
26     int vex1, vex2, weight;
27     GraphListNode *tempNode = NULL;
28     printf("请输入，输入方式为起点 终点  边上权值，点为-1，则输入结束\n");
29     scanf("%d%d%d", &vex1, &vex2, &weight);
30     while(vex1>=0 && vex2>=0)
31     {
32         tempNode = (GraphListNode*)malloc(sizeof(GraphListNode));
33         tempNode->nodeno = vex2;
34         tempNode->weight = weight;
35         tempNode->next = NULL;
36         tempNode->next = graphList->graphListArray[vex1].next;
37         graphList->graphListArray[vex1].next = tempNode;
38         scanf("%d%d%d", &vex1, &vex2, &weight);
39     }
40 }
41 
42 /* 输出图中顶点  */
43 void WriteGraph(GraphList* graphList)
44 {
45     int i;
46     GraphListNode *tempNode = NULL;
47     for (i=0; i<graphList->size; i++)
48     {
49         tempNode = graphList->graphListArray[i].next;
50         
51         while(tempNode != NULL)
52         {
53             printf("结点%d和%d相连,权值为%d\n",i,tempNode->nodeno, tempNode->weight);
54             tempNode = tempNode->next;
55         }
56     }
57 }

邻接表，graphlistutil.c

 1 /** 
 2 * @file graphinverselistutil.h
 3 * @brief 图的逆邻接表表示以及辅助函数                                                               
 4 */
 5 #ifndef GRAPHINVERSELISTUTIL_H
 6 #define GRAPHINVERSELISTUTIL_H
 7 
 8 typedef struct    GRAPHINVERSELISTNODE_STRU
 9 {
10     int nodeno;/*!< 图中结点的编号 */
11     int weight;/*!< 图中边的权值 */
12     struct    GRAPHINVERSELISTNODE_STRU* next;/*!<指向下一个结点的指针 */
13 }GraphInverseListNode;
14 
15 typedef struct    GRAPHINVERSELIST_STRU
16 {
17     int size;/*!< 图中结点的个数 */
18     GraphInverseListNode* graphInverseListArray;/*!<图的邻接表 */
19 }GraphInverseList;
20 
21 /**
22   * @brief  初始化图
23   * @param[in]   num    图中结点的个数
24   * @return    用逆邻接表表示的图
25   */
26 GraphInverseList* InitInverseGraph(int num);
27 
28 /**
29   * @brief  将数据读入图中
30   * @param[in]   graphInverseList    图
31   */
32 void ReadInverseGraph(GraphInverseList* graphInverseList);
33 
34 /**
35   * @brief  将图的结构显示出来
36   * @param[in]   graphInverseList    图
37   */
38 void WriteInverseGraph(GraphInverseList* graphInverseList);
39 
40 #endif

逆邻接表，graphinverselistutil.h

 1 /** 
 2 graphinverselistutil.c                                                           
 3 */
 4 #include "graphinverselistutil.h"
 5 #include <stdlib.h>
 6 #include <stdio.h>
 7 
 8 GraphInverseList* InitInverseGraph(int num)
 9 {
10     int i;
11     GraphInverseList *graphInverseList = (GraphInverseList *)malloc(sizeof(GraphInverseList));
12     
13     graphInverseList->size = num;
14     graphInverseList->graphInverseListArray = (GraphInverseListNode*)malloc(sizeof(GraphInverseListNode)*num);
15     
16     for (i=0; i<num; i++)
17     {
18         graphInverseList->graphInverseListArray[i].next = NULL;
19         graphInverseList->graphInverseListArray[i].nodeno = i;
20     }
21     
22     return graphInverseList;
23 }
24 
25 void ReadInverseGraph(GraphInverseList* graphInverseList)
26 {
27     int vexBegin, vexEnd, weight;
28     GraphInverseListNode *tempNode = NULL;
29     printf("请输入，输入方式为起点 终点  边上权值，点为-1，则输入结束\n");
30     scanf("%d%d%d", &vexBegin, &vexEnd, &weight);
31     
32     while(vexBegin>=0 && vexEnd>=0)
33     {
34         tempNode = (GraphInverseListNode*)malloc(sizeof(GraphInverseListNode));
35         tempNode->nodeno = vexBegin;
36         tempNode->weight = weight;
37         tempNode->next = NULL;
38         tempNode->next = graphInverseList->graphInverseListArray[vexEnd].next;
39         graphInverseList->graphInverseListArray[vexEnd].next = tempNode;
40         scanf("%d%d%d", &vexBegin, &vexEnd, &weight);
41     }
42 }
43 
44 void WriteInverseGraph(GraphInverseList* graphInverseList)
45 {
46     int i;
47     GraphInverseListNode *tempNode = NULL;
48     
49     for (i=0; i<graphInverseList->size; i++)
50     {
51         tempNode = graphInverseList->graphInverseListArray[i].next;
52         
53         while(tempNode != NULL)
54         {
55             printf("结点%d和%d相连,权值为%d\n", tempNode->nodeno, i, tempNode->weight);
56             tempNode = tempNode->next;
57         }
58     }
59 }

逆邻接表，graphinverselistutil.c

 1 /** 
 2 * @file criticalpath.h
 3 * @brief 图的关键路径                                                               
 4 */
 5 #ifndef CRITICALPATH_H_
 6 #define CRITICALPATH_H_
 7 
 8 #include "graphlistutil.h"
 9 #include "graphinverselistutil.h"
10 
11 /**
12   * @brief  事件可能的最早发生时间
13   * @param[in]   graphList 用邻接表表示的图   
14   * @param[out]   earliestTime    事件可能的最早发生时间
15   * @return   是否成功
16   */
17 int eventEarliestTime(GraphList *graphList, int* earliestTime);
18 
19 /**
20   * @brief  事件允许的最迟发生时间
21   * @param[in]   graphInverseList    用逆邻接表表示的图
22   * @param[out]   latestTime    事件允许的最迟发生时间
23   * @return    是否成功
24   */
25 int eventLatestTime(GraphInverseList *graphInverseList, int* latestTime);
26 
27 /**
28   * @brief  关键路径
29   * @param[in]   graphList 用邻接表表示的图   
30   * @param[in]   graphInverseList    用逆邻接表表示的图
31   */
32 void criticalPath(GraphList *graphList, GraphInverseList *graphInverseList);
33 
34 #endif

关键路径，criticalpath.h

  1 #include "graphlistutil.h"
  2 #include "graphinverselistutil.h"
  3 #include "linkstack.h"
  4 #include <stdio.h>
  5 #include <stdlib.h>
  6 
  7 int eventEarliestTime(GraphList *graphList, int* earliestTime)
  8 {
  9     int i;
 10     int cnt;
 11     int nodeNum;
 12     int success = 1;
 13     
 14     LinkStack nodeStack = NULL;
 15     GraphListNode *tempNode = NULL;
 16     int *inPoint = (int *)malloc(sizeof(int) * graphList->size);
 17     nodeStack = SetNullStack_Link();
 18     
 19     for (i=0; i<graphList->size; i++)
 20     {
 21         inPoint[i] = 0;
 22     }
 23     
 24     for (i=0; i<graphList->size; i++)
 25     {
 26         tempNode = graphList->graphListArray[i].next;
 27         
 28         while(tempNode != NULL)
 29         {
 30             inPoint[tempNode->nodeno]++;
 31             tempNode = tempNode->next;
 32         }
 33     }
 34 
 35     for(i=0; i<graphList->size; i++)
 36     {
 37         if (inPoint[i] == 0)
 38         {
 39             Push_link(nodeStack, i);
 40         }
 41     }
 42 
 43     cnt = 0;
 44     while(!IsNullStack_link(nodeStack))
 45     {
 46         nodeNum = Top_link(nodeStack);
 47         Pop_link(nodeStack);
 48         cnt++;
 49 
 50         tempNode = graphList->graphListArray[nodeNum].next;
 51         while(tempNode != NULL)
 52         {
 53             inPoint[tempNode->nodeno]--;
 54             if (earliestTime[tempNode->nodeno] < earliestTime[nodeNum] + tempNode->weight)
 55             {
 56                 earliestTime[tempNode->nodeno] = earliestTime[nodeNum] + tempNode->weight;
 57             }
 58             if (inPoint[tempNode->nodeno] == 0)
 59             {
 60                 Push_link(nodeStack, tempNode->nodeno);
 61             }
 62             tempNode = tempNode->next;
 63         }
 64     }
 65 
 66     if (cnt != graphList->size)
 67     {
 68         success = 0;
 69     } 
 70     
 71     return success;
 72 }
 73 
 74 int eventLatestTime(GraphInverseList* graphInverseList, int* latestTime)
 75 {
 76     int i;
 77     int cnt;
 78     int nodeNum;
 79     int success = 1;
 80     
 81     LinkStack nodeStack = NULL;
 82     GraphInverseListNode *tempNode = NULL;
 83     int *outPoint = (int *)malloc(sizeof(int) * graphInverseList->size);
 84     nodeStack = SetNullStack_Link();
 85     
 86     for (i=0; i<graphInverseList->size; i++)
 87     {
 88         outPoint[i] = 0;
 89     }
 90 
 91     for (i=0; i<graphInverseList->size; i++)
 92     {
 93         tempNode = graphInverseList->graphInverseListArray[i].next;
 94         
 95         while(tempNode != NULL)
 96         {
 97             outPoint[tempNode->nodeno]++;
 98             tempNode = tempNode->next;
 99         }
100     }
101 
102     for(i=0; i<graphInverseList->size; i++)
103     {
104         if (outPoint[i] == 0)
105         {
106             Push_link(nodeStack, i);
107         }
108     }
109 
110     cnt = 0;
111     while(!IsNullStack_link(nodeStack))
112     {
113         nodeNum = Top_link(nodeStack);
114         Pop_link(nodeStack);
115         cnt++;
116 
117         tempNode = graphInverseList->graphInverseListArray[nodeNum].next;
118         while(tempNode != NULL)
119         {
120             outPoint[tempNode->nodeno]--;
121             if (latestTime[tempNode->nodeno] > latestTime[nodeNum] - tempNode->weight)
122             {
123                 latestTime[tempNode->nodeno] = latestTime[nodeNum] - tempNode->weight;
124             }
125             if (outPoint[tempNode->nodeno] == 0)
126             {
127                 Push_link(nodeStack, tempNode->nodeno);
128             }
129             tempNode = tempNode->next;
130         }
131     }
132 
133     if (cnt != graphInverseList->size)
134     {
135         success = 0;
136     } 
137     
138     return success;
139 }
140 
141 void criticalPath(GraphList *graphList, GraphInverseList *graphInverseList)
142 {
143     int i;
144     int max;
145     
146     int* earliestTime = (int*)malloc(sizeof(int) * graphList->size);
147     int* latestTime = (int*)malloc(sizeof(int) * graphInverseList->size);
148     int activityEarliestTime;
149     int activityLatestTime;
150     
151     GraphListNode *tempNode = NULL;
152     for(i=0; i<graphList->size; i++)
153     {
154         earliestTime[i] = 0;
155     }
156     eventEarliestTime(graphList, earliestTime);
157     max = earliestTime[0];
158     for (i=0; i<graphList->size; i++)
159     {
160         if (max < earliestTime[i])
161         {
162             max = earliestTime[i];
163         }
164     }
165 
166     for(i=0; i<graphInverseList->size; i++)
167     {
168         latestTime[i] = max;
169     }
170     
171     eventLatestTime(graphInverseList, latestTime);
172     for (i=0; i<graphList->size; i++)
173     {
174         tempNode = graphList->graphListArray[i].next;
175         
176         while(tempNode != NULL)
177         {
178             activityEarliestTime = earliestTime[i];
179             activityLatestTime = latestTime[tempNode->nodeno] - tempNode->weight;
180             
181             if (activityEarliestTime == activityLatestTime)
182             {
183                 printf("<v%2d,v%2d>", i, tempNode->nodeno);
184             }
185             tempNode = tempNode->next;
186         }
187     }
188 }

关键路径，criticalpath.c

 1 #include "graphinverselistutil.h"
 2 #include "graphlistutil.h"
 3 #include "criticalpath.h"
 4 #include <stdio.h>
 5 /*
 6 0 1 14
 7 1 5 22
 8 1 2 25
 9 2 3 17
10 2 6 34
11 3 4 24
12 4 7 13
13 5 6 35
14 6 4 12
15 -1 -1 -1
16 */
17 int main()
18 {
19     GraphList *graphList = InitGraph(8);
20     GraphInverseList *graphInverseList = InitInverseGraph(8);
21     int result = 0;
22 
23     ReadGraph(graphList);
24     WriteGraph(graphList);
25 
26     ReadInverseGraph(graphInverseList);
27     WriteInverseGraph(graphInverseList);
28 
29     criticalPath(graphList, graphInverseList);
30     return 0;
31 }

测试文件，main文件

八、构建邻接表逆邻接表，DFS BFS遍历，顶点度计算

  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 #include <string.h>
  4 #include <limits.h>
  5 
  6 /******邻接矩阵表示图开始******/
  7 /* 邻接矩阵图结构体 */
  8 typedef struct GRAPHMATRIX_STRU{
  9     int size;     /* 图中结点的个数 */
 10     int **graph;   /* 二维数组指针 */
 11 }GraphMatrix;     /* 定义结构体类型 */
 12 
 13 /* 初始化图 */
 14 GraphMatrix* InitMatrixGraph(int num);
 15 
 16 /* 将数据读入图 */
 17 void ReadMatrixGraph(GraphMatrix* graphMatrix);
 18 
 19 /* 将图的结构显示出来 */
 20 void WriteMatrixGraph(GraphMatrix* graphMatrix);
 21 /******邻接矩阵表示图结束******/
 22 
 23 /*邻接表结点结构体*/
 24 typedef struct GRAPHLISTNODE_STRU
 25 {
 26     int nodeno;/* 图中结点的编号 */
 27     int weight;/* 图中边的权值 */
 28     struct    GRAPHLISTNODE_STRU* next;/* 指向下一个结点的指针 */
 29 }GraphListNode;
 30 
 31 /*邻接表图结构体*/
 32 typedef struct GRAPHLIST_STRU
 33 {
 34     int size;/* 图中结点的个数 */
 35     GraphListNode* graphListArray;/* 图的邻接表 */
 36 }GraphList;
 37 
 38 /*初始化图*/
 39 GraphList* InitGraph(int num);
 40 
 41 /*将数据读入图中*/
 42 void ReadGraph(GraphList* graphList);
 43 
 44 /*将图的结构显示出来*/
 45 void WriteGraph(GraphList* graphList);
 46 
 47 /* 深度优先搜索 */
 48 void DFS(GraphList* graphList, int *visited, int i);
 49 
 50 /* 邻接表图表示法深度优先搜索 */
 51 void DFSGraphList(GraphList* graphList);
 52 
 53 /* BFS */
 54 void BFS(GraphList* graphList, int * visited, int i);
 55 
 56 /* 邻接表BFS */
 57 void BFSGraphList(GraphList* graphList);
 58 
 59 /* 打印顶点的度 */
 60 void print(GraphList* graphList);
 61 
 62 /* 
 63 
 64 4个顶点的有向图数据
 65 
 66 邻接表
 67 
 68 1 2 4
 69 1 3 3
 70 2 3 2
 71 2 4 6
 72 3 4 4
 73 -1 -1 -1 
 74 
 75 逆邻接表
 76 
 77 2 1 4
 78 3 1 3
 79 3 2 2
 80 4 2 6
 81 4 3 4
 82 -1 -1 -1
 83 
 84 */
 85 
 86 int main()
 87 {
 88     /* 初始化4个顶点的图 */
 89     GraphList* graphList = InitGraph(4);
 90     GraphList* graphInverseList = InitGraph(4);
 91     
 92     printf("请输入邻接表数据:\n");
 93     ReadGraph(graphList);/* 输入邻接表顶点、边 */
 94     
 95     printf("请输入逆邻接表数据:\n");
 96     ReadGraph(graphInverseList);/* 输入逆邻接表顶点、边 */
 97     
 98     WriteGraph(graphList);/* 输出图的结构 */
 99     
100     DFSGraphList(graphList);/* 输出DFS遍历序列 */
101     
102     BFSGraphList(graphList);/* 输出BFS遍历序列 */
103     
104     /* 输出邻接表、逆邻接表的度 */
105     printf("\n邻接表各顶点的出度序列:\n");
106     print(graphList);
107     printf("\n逆邻接表各顶点的入度序列:\n");
108     print(graphInverseList);
109 
110     return 0;
111 }
112 
113 /* 初始化图，num表示图中结点个数，邻接表表示图 */
114 GraphList* InitGraph(int num)
115 {
116     int i;
117     /* 图空间定义 */
118     GraphList* graphList = (GraphList*)malloc(sizeof(GraphList));    
119     graphList->size = num+1;/* 图中结点数 */
120     
121     /* 邻接表数组分配空间 */
122     graphList->graphListArray = (GraphListNode*)malloc(sizeof(GraphListNode)*graphList->size); 
123     /* 邻接表数组赋值 */
124     for(i=1; i<graphList->size; ++i){
125         graphList->graphListArray[i].next = NULL;
126         graphList->graphListArray[i].nodeno = i;
127     }
128     return graphList;  /* 返回图结构体指针 */
129 }
130 
131 /* 读入图中顶点 */
132 void ReadGraph(GraphList* graphList)
133 {
134     int vex1, vex2, weight;
135     GraphListNode *tempNode = NULL;
136     /*输入方式为起点 终点  边上权值，点为-1，则输入结束 */
137     printf("请输入，输入方式为起点 终点  边上权值，点为-1，则输入结束\n");
138     scanf("%d%d%d", &vex1, &vex2, &weight);
139 
140     while(vex1>0 && vex2>0)
141     {
142         tempNode = (GraphListNode*)malloc(sizeof(GraphListNode));
143         tempNode->nodeno = vex2;
144         tempNode->weight = weight;
145         tempNode->next = NULL;
146         /* 尾插法 ,决定输出序列 */
147         tempNode->next = graphList->graphListArray[vex1].next;
148         graphList->graphListArray[vex1].next = tempNode;
149         scanf("%d%d%d", &vex1, &vex2, &weight);
150     }
151 }
152 
153 /* 输出图中顶点  */
154 void WriteGraph(GraphList* graphList)
155 {
156     int i;
157     GraphListNode* tempNodePtr = NULL;
158     printf("\n图的结构如下，输出方式为顶点，顶点\n\n");
159     for(i=1; i<graphList->size; ++i){
160         tempNodePtr = graphList->graphListArray[i].next;
161         while(tempNodePtr){
162             printf("结点%d到结点%d有边相连\n",i,tempNodePtr->nodeno);         
163             tempNodePtr = tempNodePtr->next;
164         }
165     }
166     printf("\n");
167 }
168 
169 /* 深度优先搜索 */
170 void DFS(GraphList* graphList, int *visited, int i)
171 {
172     int j;
173     GraphListNode* tempNodePtr = NULL;
174     visited[i] = 1;
175     printf("%d ",i);
176     
177     tempNodePtr = graphList->graphListArray[i].next;
178     while(tempNodePtr)
179     {
180         if(!visited[tempNodePtr->nodeno])
181             DFS(graphList,visited,tempNodePtr->nodeno);
182         tempNodePtr = tempNodePtr->next;
183     }
184 }
185 
186 /* 邻接表图表示法深度优先搜索 */
187 void DFSGraphList(GraphList* graphList)
188 {
189     int i;
190     /* 定义,用以记录顶点是否被访问的数组visited */
191     int *visited = (int*)malloc(sizeof(int)*graphList->size);
192 
193     for(i=0; i < graphList->size; ++i)
194         visited[i] = 0;    /* 初始化顶点都没有被访问 */
195 
196     for(i=1; i < graphList->size; ++i)
197         if(!visited[i])  /* 对未访问的顶点调用DFS,若是连通图,只会执行一次 */
198         {
199             printf("深度优先搜索输出序列:");
200             DFS(graphList,visited,i);
201             printf("\n\n");
202         }          
203 }
204 
205 /* BFS */
206 void BFS(GraphList* graphList, int * visited, int i)
207 {
208     int tempVex;
209     GraphListNode *tempNode = NULL;
210     
211     /*广度优先遍历使用的队列*/
212     const int MAXQSIZE = 100;
213     int waitingQueue[MAXQSIZE];
214     int front = 0, rear = 0;
215 
216     /* 如果没有访问过，则访问 */
217     if (!visited[i])    
218     {
219         /*设置标记，表明已经被访问 */
220         visited[i] = 1;    
221         /*输出访问的结点编号 */
222         printf("%d ", i);
223         /*将刚访问的结点放入队列 */
224         waitingQueue[rear] = i;
225         rear = (rear+1) % MAXQSIZE;
226 
227         /*访问结点－广度优先 */
228         while(front != rear)    
229         {
230             tempVex = waitingQueue[front];
231             front = (front+1) % MAXQSIZE;
232             
233             tempNode = graphList->graphListArray[tempVex].next;
234             while(tempNode != NULL)
235             {
236                 if(!visited[tempNode->nodeno]) 
237                 { 
238                     visited[tempNode->nodeno] = 1;
239                     waitingQueue[rear] = tempNode->nodeno;
240                     rear = (rear+1) % MAXQSIZE;           
241                     printf("%d ", tempNode->nodeno);
242                 }
243                 tempNode = tempNode->next;
244             }
245         }
246     }
247 }
248 
249 /* 邻接表BFS */
250 void BFSGraphList(GraphList* graphList)
251 {
252     int i;
253 
254     /*用于记录图中哪些结点已经被访问了 */
255     int *visited = (int*)malloc(sizeof(int) * graphList->size);
256 
257     /*设置所有结点都没有被访问，其中1为访问过，0为没有被访问 */
258     for(i = 0; i < graphList->size; i++)
259         visited[i] = 0;
260 
261     /* 从1号结点开始进行广度优先遍历 */
262     for(i = 1; i < graphList->size; i++)  
263     {        
264         if(!visited[i])
265         {
266             printf("广度优先遍历输出序列:");
267             BFS(graphList, visited, i);
268             printf("\n\n");
269         }       
270     }
271 }
272 
273 void print(GraphList* graphList)
274 {
275     for (int i=1; i<graphList->size; i++)
276     {
277         printf("顶点%d:",i);
278         GraphListNode *tempNode = graphList->graphListArray[i].next;
279         if(!tempNode) printf(" -");
280         while(tempNode != NULL)
281         {
282             printf(" %d",tempNode->nodeno);
283             tempNode = tempNode->next;
284         }
285         printf("\n");
286     }
287 }
288 
289 /******邻接矩阵表示图开始******/
290 /* 初始化图，num表示图中结点个数，邻接矩阵表示图 */
291 GraphMatrix* InitMatrixGraph(int num)
292 {
293     int i,j;
294     /* 图空间定义 */
295     GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix));    
296     graphMatrix->size = num;/* 图中结点数 */
297     
298     /* 指针数组分配空间 */
299     graphMatrix->graph = (int**)malloc(sizeof(int*)*graphMatrix->size);
300     /* 指针数组中的指针分配空间 */
301     for(i=0; i<graphMatrix->size; ++i){
302         graphMatrix->graph[i] = (int*)malloc(sizeof(int*)*graphMatrix->size);
303     }
304     
305     /* 图中所有元素赋值 */
306     for(i=0; i<graphMatrix->size; ++i){
307         for(j=0; j<graphMatrix->size; ++j){
308             graphMatrix->graph[i][j] = INT_MAX;
309         }
310     }
311     return graphMatrix;  /* 返回图结构体指针 */
312 }
313 
314 /* 读入图中顶点，权值 */
315 void ReadMatrixGraph(GraphMatrix* graphMatrix)
316 {
317     int vex1,vex2,weight;
318     printf("请输入顶点，顶点，权值，权值为0，则输入结束\n");
319     scanf("%d%d%d", &vex1, &vex2, &weight);
320     while(weight)
321     {
322         graphMatrix->graph[vex1][vex2] = weight;
323         scanf("%d%d%d", &vex1, &vex2, &weight);
324     }
325 }
326 
327 /* 输出图中顶点，权值  */
328 void WriteMatrixGraph(GraphMatrix* graphMatrix)
329 {
330     int i,j;
331     printf("图的结构如下，输出方式为顶点，顶点，权值\n");
332     for(i=0; i<graphMatrix->size; ++i){
333         for(j=0; j<graphMatrix->size; ++j){
334             if(graphMatrix->graph[i][j] < INT_MAX){
335                 printf("%d,%d,%d\n",i,j,graphMatrix->graph[i][j]);
336             }
337         }
338     }
339 }
340 /******邻接矩阵表示图结束******/

BFS DFS遍历，输出顶点的度

刷新页面返回顶部

金色省略号的个人博客

图的概念、存储、遍历、最短路径问题、最小生成树、拓扑排序、关键路径