一、哈夫曼树,最优二叉树,WPL最小的二叉树
带权路径长度(WPL):
设二叉树有n个叶子结点,每个叶子结点带 有权值 wk,从根结点到每个叶子结点的长度为 lk,则每个叶子结点的带权路径长度之和WPL
哈夫曼树的特点:
1、没有度为1的结点;
2、哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树;
3、n个叶子结点的哈夫曼树共有2n-1个结点(由没有度为1的结点推出, n0+n1+n2 = 2*n0-1);
4、对同一组权值{w1 ,w2 , …… , wn},存在不同构的两棵哈夫曼树;
5、外部结点的个数比内部结点的个数多一;
二、堆的两个特性
结构性:用数组表示的完全二叉树;
有序性:任一结点的关键字是其子树所有结点的最大值(或最小值)
(堆的结点的子结点之间没有关系)
1、堆的操作

1 typedef struct HNode *Heap; /* 堆的类型定义 */ 2 struct HNode { 3 ElementType *Data; /* 存储元素的数组 */ 4 int Size; /* 堆中当前元素个数 */ 5 int Capacity; /* 堆的最大容量 */ 6 }; 7 typedef Heap MaxHeap; /* 最大堆 */ 8 typedef Heap MinHeap; /* 最小堆 */ 9 10 #define MAXDATA 1000 /* 该值应根据具体情况定义为大于堆中所有可能元素的值 */ 11 12 MaxHeap CreateHeap( int MaxSize ) 13 { /* 创建容量为MaxSize的空的最大堆 */ 14 15 MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode)); 16 H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType)); 17 H->Size = 0; 18 H->Capacity = MaxSize; 19 H->Data[0] = MAXDATA; /* 定义"哨兵"为大于堆中所有可能元素的值*/ 20 21 return H; 22 } 23 24 bool IsFull( MaxHeap H ) 25 { 26 return (H->Size == H->Capacity); 27 } 28 29 bool Insert( MaxHeap H, ElementType X ) 30 { /* 将元素X插入最大堆H,其中H->Data[0]已经定义为哨兵 */ 31 int i; 32 33 if ( IsFull(H) ) { 34 printf("最大堆已满"); 35 return false; 36 } 37 i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */ 38 for ( ; H->Data[i/2] < X; i/=2 ) 39 H->Data[i] = H->Data[i/2]; /* 上滤X */ 40 H->Data[i] = X; /* 将X插入 */ 41 return true; 42 } 43 44 #define ERROR -1 /* 错误标识应根据具体情况定义为堆中不可能出现的元素值 */ 45 46 bool IsEmpty( MaxHeap H ) 47 { 48 return (H->Size == 0); 49 } 50 51 ElementType DeleteMax( MaxHeap H ) 52 { /* 从最大堆H中取出键值为最大的元素,并删除一个结点 */ 53 int Parent, Child; 54 ElementType MaxItem, X; 55 56 if ( IsEmpty(H) ) { 57 printf("最大堆已为空"); 58 return ERROR; 59 } 60 61 MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */ 62 /* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */ 63 X = H->Data[H->Size--]; /* 注意当前堆的规模要减小 */ 64 for( Parent=1; Parent*2<=H->Size; Parent=Child ) { 65 Child = Parent * 2; 66 if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) ) 67 Child++; /* Child指向左右子结点的较大者 */ 68 if( X >= H->Data[Child] ) break; /* 找到了合适位置 */ 69 else /* 下滤X */ 70 H->Data[Parent] = H->Data[Child]; 71 } 72 H->Data[Parent] = X; 73 74 return MaxItem; 75 } 76 77 /*----------- 建造最大堆 -----------*/ 78 void PercDown( MaxHeap H, int p ) 79 { /* 下滤:将H中以H->Data[p]为根的子堆调整为最大堆 */ 80 int Parent, Child; 81 ElementType X; 82 83 X = H->Data[p]; /* 取出根结点存放的值 */ 84 for( Parent=p; Parent*2<=H->Size; Parent=Child ) { 85 Child = Parent * 2; 86 if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) ) 87 Child++; /* Child指向左右子结点的较大者 */ 88 if( X >= H->Data[Child] ) break; /* 找到了合适位置 */ 89 else /* 下滤X */ 90 H->Data[Parent] = H->Data[Child]; 91 } 92 H->Data[Parent] = X; 93 } 94 95 void BuildHeap( MaxHeap H ) 96 { /* 调整H->Data[]中的元素,使满足最大堆的有序性 */ 97 /* 这里假设所有H->Size个元素已经存在H->Data[]中 */ 98 99 int i; 100 101 /* 从最后一个结点的父节点开始,到根结点1 */ 102 for( i = H->Size/2; i>0; i-- ) 103 PercDown( H, i ); 104 }
2、堆的操作实例
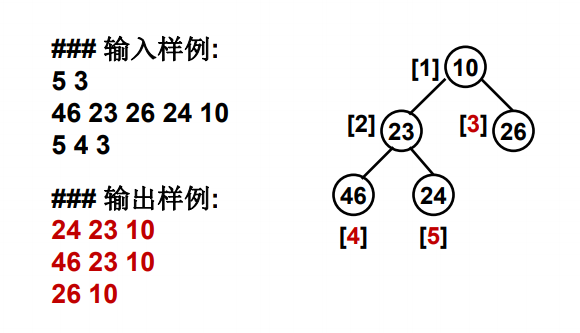
堆的路径,将一系列给定数字插入一个初始为空的小顶堆H[]。
随后对任意给 定的下标`i`,打印从H[i]到根结点的路径。

1 #include <stdio.h> 2 /* 1.定义堆H */ 3 #define MAXN 1001 4 #define MINH -10001 5 int H[MAXN], size;//堆,堆的大小 6 /* 2.堆的初始化 */ 7 void Create () 8 { 9 size = 0; 10 H[0] = MINH;/*设置“岗哨”*/ 11 } 12 /* 3.堆插入 */ 13 void Insert ( int X ) 14 { 15 /* 省略检查堆是否已满 */ 16 int i; //46 23 26 24 10 17 /* 18 下标从1开始,逐个插入, 19 插入过程,从后向前,逐个与其父结点比较 20 父结点大, 上滤X 21 1 2 3 4 5 22 46 <-46 1/2==0 0 23 23 46 <-23 2/2==1 1 0 24 23 46 26 <-26 3/2==1 1 0 25 23 24 26 46 <-24 4/2==2 2 1 0 26 10 23 26 46 24 <-10 5/2==2 2 1 0 27 */ 28 for (i=++size; H[i/2] > X; i/=2) 29 H[i] = H[i/2]; 30 H[i] = X;//将X插入H 31 } 32 33 int main() 34 { 35 /* 36 读入n和m 37 根据输入序列建堆 38 对m个要求:打印到根的路径 39 5 3 40 46 23 26 24 10 41 5 4 3 42 */ 43 int n, m, x, i, j; 44 scanf("%d%d", &n, &m); 45 Create(); /* 堆初始化 */ 46 for (i=0; i<n; i++) { 47 scanf("%d", &x); 48 Insert(x); /*以逐个插入方式建堆 */ 49 } 50 51 /* for(int i=1; i<=n; ++i) 52 printf("%3d",H[i]); */ 53 54 /* m个结点 */ 55 for (i=0; i<m; i++) 56 { 57 scanf("%d", &j);//具体结点 58 printf("%d", H[j]); 59 /*向根方向输出各结点*/ 60 while (j>1) { 61 j /= 2; 62 printf(" %d", H[j]); 63 } 64 printf("\n"); 65 } 66 return 0; 67 }
三、C++ 根据给定的权值创建,哈夫曼树 (用到优先队列,贪心算法,青岛大学mooc)
学友代码

#include <iostream> #include <map> #include<algorithm> #include <queue> #define MAX 500 using namespace std; int n; //哈夫曼树中结点的类型 struct HuffmanTree { char data; int weight; int parent, lchild, rchild; }; HuffmanTree HT[MAX]; //y优先队列结点类型 struct NodeType { int now;//对应哈夫曼树中的位置(数组下标) char data; int weight; bool operator<(const NodeType& s) const//(小顶堆) { return s.weight < weight; } }; priority_queue<NodeType > qu; void CreatHuffmanTree() { NodeType e, e1, e2; cout << "请输入构建的哈夫曼树的元素以及对应权值:" << endl; for (int i = 0; i < n; i++) { cin >> HT[i].data >> HT[i].weight; } //将n个结点进队 for(int i=0;i<n;i++) { e.now = i; e.data = HT[i].data; e.weight = HT[i].weight; qu.push(e); } //初始化结点的指针域 for (int i = 0; i < 2*n-1; i++) { HT[i].parent = HT[i].lchild = HT[i].rchild = -1; } //构造huffman树剩余结点(求和得到的结点) for(int j=n;j<2*n-1;j++) { e1 = qu.top();//访问最小 qu.pop(); e2 = qu.top();//访问次小 qu.pop(); HT[j].weight = e1.weight + e2.weight; HT[j].lchild = e1.now; HT[j].rchild = e2.now; HT[e1.now].parent = j;//最小的结点的parent为n号位置上的结点 HT[e2.now].parent = j;//次小也是 e.now = j;//构造新结点 e.weight = e1.weight + e2.weight; qu.push(e); } } void HuffmmanCode() { string code; for(int i=0;i<n;i++) { code = ""; int curnow = i; int f = HT[curnow].parent;//当前结点的parent不是根结点就往上找(直到到达根结点,就可以得到哈夫曼编码的倒序) while(f!=-1)//构造好的huffman树只有根节点没有parent,因此根节点的parent为-1 { if (HT[f].lchild == curnow) code += '0'; else code += '1'; curnow = f; f = HT[curnow].parent; } cout << HT[i].data << " "; reverse(code.begin(), code.end() ); cout << code << endl; } } int main() { cout << "请输入要构建哈夫曼树的元素个数:"; freopen("d:\\1.txt","r",stdin ); cin >> n; CreatHuffmanTree(); cout << "哈夫曼编码为:" << endl; HuffmmanCode(); return 0; }
修改青岛大学代码

#include <iostream> #include <vector> #include <queue> #include <map> using namespace std; struct Node{ char ch; int data; Node* left; Node* right; Node(){ left = right= NULL;} Node(char ch, int data):ch(ch),data(data){ left = right = NULL; } }; struct HuffmanTree{ Node* root; HuffmanTree(){root = NULL;} HuffmanTree(char ch, int weight){ root = new Node(ch,weight); } HuffmanTree(vector<HuffmanTree> &nodes){ priority_queue<HuffmanTree, vector<HuffmanTree>, greater<HuffmanTree>> q(nodes.begin(),nodes.end()); HuffmanTree tmp; for(int i=1; i<nodes.size();++i){ tmp.root = new Node(); tmp.root->left = q.top().root; q.pop(); tmp.root->right = q.top().root; q.pop(); tmp.root->data = tmp.root->left->data + tmp.root->right->data; q.push(tmp); } root = q.top().root; } bool operator > (const HuffmanTree &t) const{ return this->root->data > t.root->data; } void print(){ rprint(root,0); } void rprint(Node* r, int depth){ for(int i=0; i<depth; ++i) cout<<" "; if(!r) cout<<"[/]"<<endl; else{ cout<<r->data<<endl; rprint(r->left, depth+1); rprint(r->right,depth+1); } } //huffman编码 map<string, char > HuffmanCode; void createHuffmanCode(Node* root, string tmp ){ if(root->left==NULL && root->right==NULL ){ HuffmanCode[tmp] = root->ch; return; } createHuffmanCode(root->left, tmp+="0"); tmp.pop_back(); createHuffmanCode(root->right, tmp+="1"); tmp.pop_back(); } //打印编码 void printHuffmanCode(){ string tmp; createHuffmanCode(root,tmp ); map<char, string > t; for(map<string, char >::iterator it = HuffmanCode.begin(); it != HuffmanCode.end(); ++it ) t[it->second] = it->first; for(map<char, string >::iterator it = t.begin(); it != t.end(); ++it ) cout << it->first << " " << it->second << endl; } }; int main() { freopen("d:\\1.txt","r",stdin ); int nv,weight; char ch; cin>>nv; vector<HuffmanTree> nodes; for(int i=0; i<nv; ++i){ cin>> ch >> weight; nodes.emplace_back(ch,weight); } HuffmanTree ht(nodes); //ht.print(); ht.printHuffmanCode(); return 0; }
青岛大学代码

#include <iostream> #include <vector> #include <queue> using namespace std; struct Node{ int data; Node* left; Node* right; Node(){ left = right= NULL;} Node(int data){ this->data = data; left = right = NULL; } }; struct HuffmanTree{ Node* root; HuffmanTree(){root = NULL;} HuffmanTree(int weight){ root = new Node(weight); } HuffmanTree(vector<HuffmanTree> &nodes){ priority_queue<HuffmanTree, vector<HuffmanTree>, greater<HuffmanTree>> q(nodes.begin(),nodes.end()); HuffmanTree tmp; for(int i=1; i<nodes.size();++i){ tmp.root = new Node(); tmp.root->left = q.top().root; q.pop(); tmp.root->right = q.top().root; q.pop(); tmp.root->data = tmp.root->left->data + tmp.root->right->data; q.push(tmp); } root = q.top().root; } bool operator > (const HuffmanTree &t) const{ return this->root->data > t.root->data; } void print(){ rprint(root,0); } void rprint(Node* r, int depth){ for(int i=0; i<depth; ++i) cout<<" "; if(!r) cout<<"[/]"<<endl; else{ cout<<r->data<<endl; rprint(r->left, depth+1); rprint(r->right,depth+1); } } }; int main() { int nv,weight; cin>>nv; vector<HuffmanTree> nodes; for(int i=0; i<nv; ++i){ cin>>weight; nodes.emplace_back(weight); } HuffmanTree ht(nodes); ht.print(); return 0; } /* 7 10 15 12 3 4 13 1 */




