一、朴素模式匹配

#include <stdio.h> #include <stdlib.h> /* 在源串S中查找目标串T,如没有找到则打印出错信息; 否则,在第一次匹配后请将源串S的匹配部分就地逆置 */ typedef char elementype; typedef struct node { elementype data; struct node * next; }linkstr; linkstr* createstr(); void printstr(linkstr* s); void reverse(linkstr* s,linkstr* e); void match(linkstr* s,linkstr* t); int main() { /*输入源串 */ linkstr* head = createstr(); /* 输入目标串 */ linkstr* t = createstr(); /* 匹配 */ match(head,t); /* 打印源串 */ printstr(head); return 0; } /* create */ linkstr* createstr() { linkstr* head, *p; /* 头结点 */ head = p = (linkstr*)malloc(sizeof(linkstr)); printf("input the string\n"); char ch; linkstr* tmp = NULL; while((ch=getchar())!='\n') { tmp = (linkstr*)malloc(sizeof(linkstr)); tmp->data = ch; tmp->next = NULL; p->next = tmp; p = p->next; } return head; } /* 打印 */ void printstr(linkstr* p) //输出串 { p = p->next; /* 有头结点 */ while(p) { printf("%c",p->data); p = p->next; } } /* 逆序 */ void reverse(linkstr* s,linkstr* e) { linkstr* CUR = s->next, *NEW; s->next = e; /* s为逆序字符串的前驱结点 */ while(CUR!=e) { NEW = CUR; /* 保存当前指针 */ CUR = CUR->next; /* 当前指针更新(为新表的前驱) */ NEW->next = s->next; /* 新结点头插法 */ s->next = NEW; /* 新结点插到头结点 */ } } /* 匹配 */ void match(linkstr* s,linkstr* t) { linkstr* pre = s; /* pre 为逆序需要,保存匹配字符串前驱位置 */ linkstr* begin = s->next;//begin 源串与目标串比较的位置 linkstr* p, *q; p = begin, q = t->next; /* p,q 源串、目标串比较开始位置 */ while(p&&q)/* 在第一次匹配后 */ { if (p->data==q->data) { p = p->next; q = q->next; } else { pre = begin; /* 匹配字符串前驱位置 */ begin = begin->next; p = begin; /* 更新源串 目标串比较位置 */ q = t->next; } } if (q==NULL) /* 匹配 */ { reverse(pre,p); /* 匹配部分逆序 */ } else printf("error!\n"); }
二、KMP算法,用于在一个字符串S中查找一个模式串P 的出现位置,当字符串S下标 i 的字符与模式串P下标 j 的字符失配时,i 不回溯,算法复杂度为O(n+m)。
1、算法利用了模式串P下标 j 之前的字符(P的子串)与字符串S是匹配的这个重要信息。
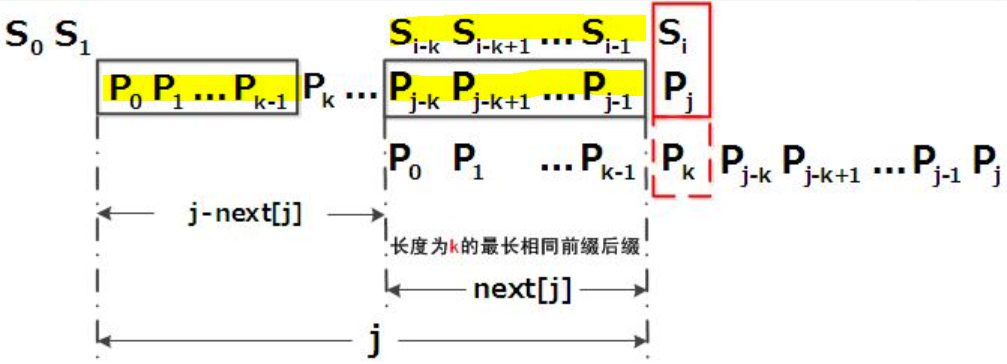
2、模式串P所有子串的对称程度,决定着模式串P的右移
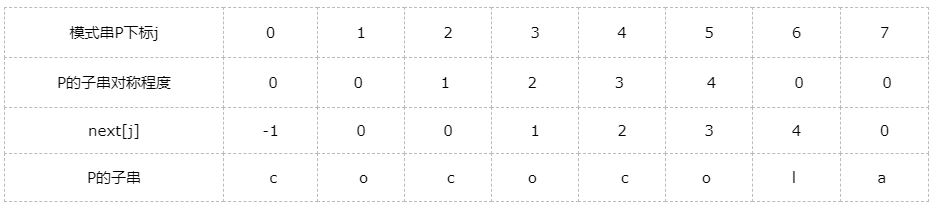
这个对称不是中心对称,是子串的左子串与最大前缀子串相等的对称,我们看上面表格,模式串P的子串coco,子串的左子串下标2~3的co与最大前缀子串下标0~1的co是对称的,对称程度是2。next[j],是在模式串P下标 j 的字符失配的时候,P下标 j-1的对称程度,比如P[6]失配,P[5]的对称程度为4(最大前缀4),P下标4的字符(P的第5个字符c)与S下标 i 的字符继续比较。
(1)计算模式串P的子串的对称程度,以上面的表格为例,P下标0的对称程度为0,下标1的字符o与子串的第一个前缀字符c不等,对称程度为0,下标2的字符c与第一个前缀字符c相等,对称程度为1,下标3的字符o与第二个前缀字符o相等,对称加1,为2,...,只要当前字符与前缀字符依次相等,可以继承上个字符的对称程度加1,一旦失配,要重新计算对称程度,这个重新计算的对称程度一定比左边的对称程度低,不代表没有对称程度,低到什么程度,依次向左递归比较。
比如P[6],我们看P[5]的对称程度为4,P[6] != P[4]失配了,P[4]的对称程度为3,P[6] != P[3]失配了,我们看P[3]的对称程度为2,P[6] != P[2]失配了,我们看P[2]的对称程度为1,P[6] != P[1]失配了,我们看P[1]的对称程度为0,P[6] 的对称程度为0;假如P[6]字符 'l' 换成字符 'c',我们看P[5]的对称程度为4,P[6] == P[4],那么,P[6]的对称程度继承P[5]的对称程度,4+1==5;假如,P[6]还是字符 'l',P[7]字符 'a' 换成字符 'c',我们看P[6]的对称程度为0,P[7] == P[0],那么,P[7]的对称程度继承P[6]的对称程度,0+1==1
(2)计算next数组,是模式串P的各个子串的对称程度右移一位,next[0] = -1。 算法实现,设 j =0, k = -1, next[0] = -1; 若k==-1或者P[k] == P[j],j++,k++, next[j] = k; 否则递归,k=next[k]; 我们为什么计算next数组,因为next[j]是失配的,所以,next[j]记录的应该是P[j-1]的对称程度;next数组决定了模式串的具体是哪一个字符与字符串S继续比较;对称的部分不需要比较了,因为对称的部分是与字符串S匹配的,例如:对称程度如果是1(模式串下标为0的元素与下标为j-1元素匹配),模式串下标1的元素与字符串S比较。

1 int* findNext(string P) 2 { 3 int j, k; 4 int m = P.length( ); // m为模式P的长度 5 assert( m > 0); // 若m=0,退出 6 int *next = new int[m]; // 动态存储区开辟整数数组 7 assert( next != 0); // 若开辟存储区域失败,退出 8 next[0] = -1; 9 j = 0; k = -1; 10 while (j < m-1) 11 { 12 if(k == -1 || P[k] == P[j]){ 13 next[++j] = ++k; 14 } 15 else 16 k = next[k]; 17 } 18 return next; 19 }

1 #include <iostream> 2 #include <string> 3 #include <cassert> 4 using namespace std; 5 6 int KMPStrMatching(string S, string P, int *N, int start) 7 { 8 int j= 0; // 模式的下标变量 9 int i = start; // 目标的下标变量 10 int pLen = P.length( ); // 模式的长度 11 int tLen = S.length( ); // 目标的长度 12 if (tLen - start < pLen) // 若目标比模式短,匹配无法成功 13 return (-1); 14 while ( j < pLen && i < tLen) 15 { // 反复比较,进行匹配 16 if ( j == -1 || S[i] == P[j]) 17 i++, j++; 18 else j = N[j]; 19 } 20 if (j >= pLen) 21 return (i-pLen); // 注意仔细算下标 22 else return (-1); 23 } 24 25 int* findNext(string P) 26 { 27 int j, k; 28 int m = P.length( ); // m为模式P的长度 29 assert( m > 0); // 若m=0,退出 30 int *next = new int[m]; // 动态存储区开辟整数数组 31 assert( next != 0); // 若开辟存储区域失败,退出 32 next[0] = -1; 33 j = 0; k = -1; 34 while (j < m-1) 35 { 36 if(k == -1 || P[k] == P[j]){ 37 j++; k++; next[j] = k; 38 } 39 else 40 k = next[k]; //不等则采用 KMP 递归找首尾子串 41 } 42 return next; 43 } 44 45 int main() 46 { 47 string s1 = "cocococola"; 48 string s2 = "cococola"; 49 int ret = KMPStrMatching(s1,s2,findNext(s2),0); 50 cout << ret <<endl; 51 return 0; 52 }

1 #include <stdio.h> 2 #include <string.h> 3 #include <malloc.h> 4 5 int* findNext(const char* P) 6 { 7 int j, k; 8 int m = strlen(P); // m为模式P的长度 9 10 int *next = (int*)malloc(sizeof(int)*m); // 动态存储区开辟整数数组 11 12 next[0] = -1; 13 j = 0; k = -1; 14 while (j < m-1) 15 { 16 if(k == -1 || P[k] == P[j]){ 17 next[++j] = ++k; 18 } 19 else 20 k = next[k]; 21 } 22 return next; 23 } 24 25 int main() 26 { 27 const char *s = "ababaaababaa"; //"aaab";//"abaabcac";//"abcaabbcabcaabdab"; 28 int len = strlen(s); 29 int* r = findNext(s); 30 for(int i=0; i<len; ++i) 31 printf("%2d",r[i]); 32 return 0; 33 }

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 5 typedef int Position; 6 #define NotFound -1 7 8 void BuildMatch( char *pattern, int *match ) 9 { 10 Position i, j; 11 int m = strlen(pattern); 12 match[0] = -1; 13 14 for ( j=1; j<m; j++ ) { 15 i = match[j-1]; 16 while ( (i>=0) && (pattern[i+1]!=pattern[j]) ) 17 i = match[i]; 18 if ( pattern[i+1]==pattern[j] ) 19 match[j] = i+1; 20 else match[j] = -1; 21 } 22 } 23 24 Position KMP( char *string, char *pattern ) 25 { 26 int n = strlen(string); 27 int m = strlen(pattern); 28 Position s, p, *match; 29 30 if ( n < m ) return NotFound; 31 match = (Position *)malloc(sizeof(Position) * m); 32 BuildMatch(pattern, match); 33 s = p = 0; 34 while ( s<n && p<m ) { 35 if ( string[s]==pattern[p] ) { 36 s++; p++; 37 } 38 else if (p>0) p = match[p-1]+1; 39 else s++; 40 } 41 return ( p==m )? (s-m) : NotFound; 42 } 43 44 int main() 45 { 46 char string[] = "This is a simple example."; 47 char pattern[] = "simple"; 48 Position p = KMP(string, pattern); 49 if (p==NotFound) printf("Not Found.\n"); 50 else printf("%s\n", string+p); 51 return 0; 52 }
三、Rabin Karp算法
计算模式串P的哈希值,同长度字符串T的哈希值,遍历字符串T,利用之前计算过的哈希值滚动计算哈希值,如果两个哈希值相等,判断字符串与模式串是否匹配,哈希值的计算,系数的基数为31(利于代码优化),模 1000000007

/* Rabin Karp 字符串匹配算法 1、在hashcode中,总而言之就是要产生尽可能不重复的hashCode值 2、计算hashcode,用31作为系数的基数,是因为31有个很好的性能: 即用移位和减法来代替乘法 31 * h == (h << 5) - h 3、滚动哈希值计算 4、字符串匹配,哈希值一定相等 哈希值相等,字符串不一定匹配,因此需要strncmp */ #include <stdio.h> #include <string.h> #include <math.h> int main() { int i,j; char source[]= "abcdeabcdeabcde"; //T char value[] = "abcde"; //P long int mod = 1000000007; //模 long int t = 0; //T hash long int h = 0; //P hash const int len = strlen(value); //P长度len //计算哈希值的系数基数 31,最大系数31^(len-1) long int p = 1; for(j=0; j<len-1; ++j) //!!! len-1 { p = ( p * 31 ) % mod; } if (h == 0 && len > 0) { //abcde //a*31^4+b*31^3+c*31^2+d*31^1+e*31^0 for (i = 0; i < len; i++) { h = (31 * h + value[i]) %mod; //模式P的哈希值计算 t = (31 * t + source[i])%mod; //同长度字符串哈希值计算 } } //哈希值如果相等,判断字符串与模式串是否匹配 if( h == t && 0==strncmp(source,value,len) ) { printf("yes\n"); } for( ; source[i]; ++i ) { //滚动计算字符串哈希值 ( 利用之前计算过的字符串哈希值 ) t -= ( p * source[i-len] )% mod; //减去最高位的哈希值 // t += t<0 ? mod : 0; //哈希值为负数+模 t = (31 * t + source[i]) % mod; //基数 * 减去最高位的哈希值 + 后续的一个字符 //哈希值如果相等,判断字符串与模式串是否匹配 if( h == t && 0==strncmp(source+i-len+1,value,len) ) { printf("yes\n"); } } return 0; }
简化代码 ( 匹配开始的下标 i - len + 1 )

/* Rabin Karp 字符串匹配算法 1、在hashcode中,总而言之就是要产生尽可能不重复的hashCode值 2、计算hashcode,用31作为系数的基数,是因为31有个很好的性能: 即用移位和减法来代替乘法 31 * h == (h << 5) - h 3、滚动哈希值计算 4、字符串匹配,哈希值一定相等 哈希值相等,字符串不一定匹配,因此需要strncmp */ #include <stdio.h> #include <string.h> #include <math.h> int main() { int i,j; char source[]= "abcdeabcdeabcde"; //T char value[] = "abcd"; //P long int mod = 1000000007; //模 long int t = 0; //T hash long int h = 0; //P hash const int len = strlen(value); //P长度len //计算哈希值的系数基数 31,最大系数31^(len-1) long int p = 1; for(j=0; j<len-1; ++j) //!!! len-1 { p = ( p * 31 ) % mod; } if (h == 0 && len > 0) { //abcde //a*31^4+b*31^3+c*31^2+d*31^1+e*31^0 for (i = 0; i < len; i++) { h = (31 * h + value[i]) %mod; //模式P的哈希值计算 } } for( i=0; source[i]; ++i ) //遍历字符串T { //滚动计算字符串哈希值 ( 利用之前计算过的字符串哈希值 ) if(i>=len) t -= ( p * source[i-len] )% mod; //减去最高位的哈希值 t = (31 * t + source[i]) % mod; //基数 * 减去最高位的哈希值 + 后续的一个字符 //哈希值如果相等,判断字符串与模式串是否匹配 if( h == t && 0==strncmp(source+i-len+1,value,len) ) { printf("yes\n"); } } return 0; }




