c语言数字图像处理(四):灰度变换
灰度变换
灰度变换函数 s = T(r) 其中r为输入图像在(x, y)点处的灰度值,s为输出图像在(x, y)点处的灰度值
灰度变换的作用
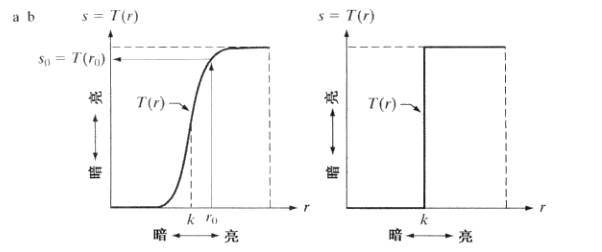
上图所示的两幅T(s)函数的图像曲线,第一幅图可以增强图像对比度,第二幅图可以对图像进行二值化处理
灰度变换函数
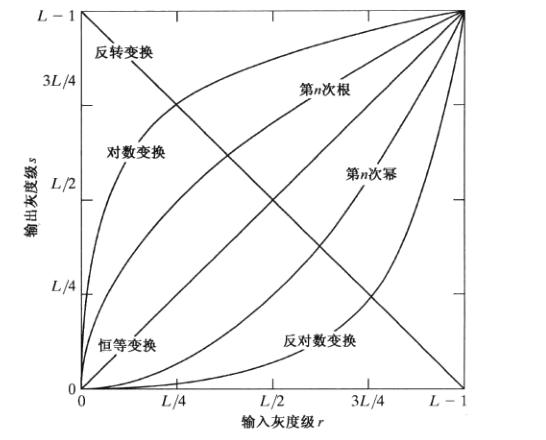
反转函数
1 void reverse(short** in_array, short** out_array, long height, long width) 2 { 3 for (int i = 0; i < height; i++){ 4 for (int j = 0; j <width; j++) 5 out_array[i][j] = GRAY_LEVELS - in_array[i][j]; 6 } 7 }
最简单的灰度变换函数,将图像中的每个像素点处的颜色值反转,对于8位灰度图片,用255减去原灰度值
原图

反转图

对数变换
s = clog(1 + r) c为常数,本次测试中c取10
1 void logarithm(short** in_array, short** out_array, long height, long width) 2 { 3 for (int i = 0; i < height; i++){ 4 for (int j = 0; j <width; j++) 5 out_array[i][j] = (short)(10 * log((1 + in_array[i][j]))); 6 } 7 }

可以看出,对数变换降低了图像的对比度
幂律(伽马)变换
s = crγ 其中 c 和 γ 为正常数

其中γ<1时,降低对比度,γ>1时,提高对比度
γ = 1.2
1 void gamma(short** in_array, short** out_array, long height, long width) 2 { 3 for (int i = 0; i < height; i++){ 4 for (int j = 0; j <width; j++) 5 out_array[i][j] = (short)pow(in_array[i][j], 1.2); 6 } 7 }

直方图均衡化
直方图为离散函数h(rk) = nk, 其中rk是第k级灰度值,nk是图像中h灰度为rk的像素个数
现在给出上面几幅图像的直方图



可以明显看出,对比度越高的图像,直方图的分布越均衡,因此直方图均衡化算法可以显著提高图像对比度
直方图均衡化算法推导(需一定高等数学及概率论知识)

算法实现
1 void calculate_histogram(long height, long width, short **image, unsigned long histogram[]) 2 { 3 short k; 4 for(int i=0; i < height; i++){ 5 for(int j=0; j < width; j++){ 6 k = image[i][j]; 7 histogram[k] = histogram[k] + 1; 8 } 9 } 10 } 11 12 void histogram_equalization(short** in_array, short** out_array, long height, long width) 13 { 14 unsigned long sum, sum_of_h[GRAY_LEVELS]; 15 double constant; 16 unsigned long histogram[GRAY_LEVELS] = {}; 17 18 calculate_histogram(height, width, in_array, histogram); 19 sum = 0; 20 for(int i=0; i < GRAY_LEVELS; i++){ 21 sum = sum + histogram[i]; 22 sum_of_h[i] = sum; 23 } 24 25 constant = (double)(GRAY_LEVELS)/(double)(height*width); 26 for(int i = 0, k = 0; i < height; i++){ 27 for(int j = 0; j < width; j++){ 28 k = in_array[i][j]; 29 out_array[i][j] = sum_of_h[k] * constant; 30 } 31 } 32 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号