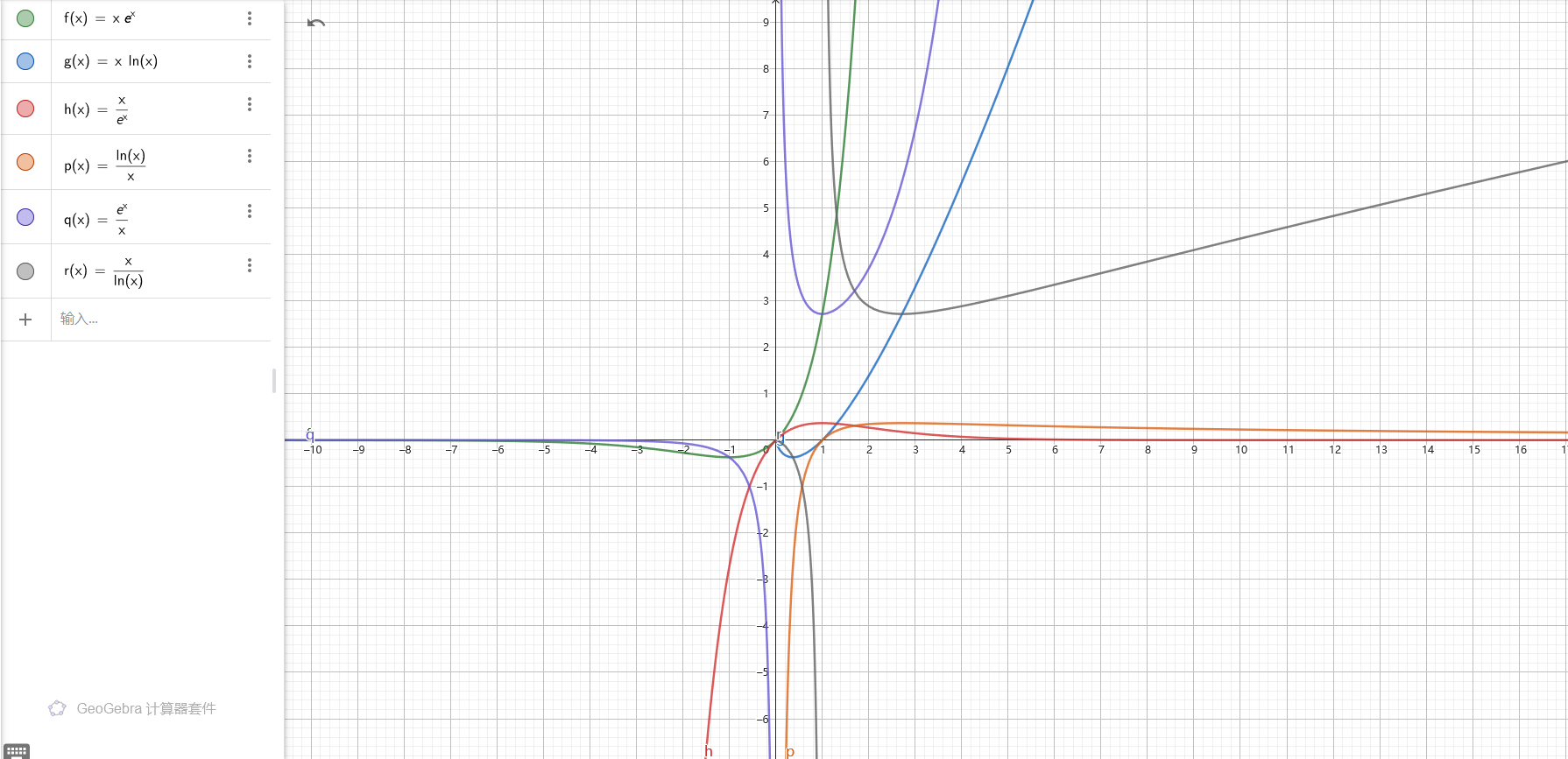
[安乐椅#10] 六小函数

1. \(f(x)=xe^x\)

定义域 \(\mathbf{R}\)

单增区间 \((-1,+\infty]\)，单减区间 \([-\infty,-1)\).

极（最）小值点 \((-1,-\dfrac{1}{e})\)

2. \(f(x)=x\operatorname{ln}x\)

定义域 \(\mathbf{R}^+\)

单增区间 \((\dfrac{1}{e},+\infty]\)，单减区间 \((0,\dfrac{1}{e})\).

极（最）小值点 \((\dfrac{1}{e},-\dfrac{1}{e})\)

3. \(f(x)=\dfrac{x}{e^x}\)

定义域 \(\mathbf{R}\)

单增区间 \([-\infty,1)\)，单减区间 \((1,+\infty]\).

极（最）大值点 \((1,\dfrac{1}{e})\)

4. \(f(x)=\dfrac{\operatorname{ln}x}{x}\)

定义域 \(\mathbf{R}^+\)

单增区间 \((0,e)\)，单减区间 \((e,+\infty]\).

极（最）大值点 \((e,\dfrac{1}{e})\)

5. \(f(x)=\dfrac{e^x}{x}\)

定义域 \(\mathbf{R}\setminus\{0\}\)

单增区间 \((1,+\infty)\)，单减区间 \((-\infty,0),(0,1)\).

极小值点 \((1,e)\)

6. \(f(x)=\dfrac{x}{\operatorname{ln}x}\)

定义域 \(\mathbf{R}^+\setminus\{1\}\)

单增区间 \((e,+\infty)\)，单减区间 \((0,1),(1,e)\).

极小值点 \((e,e)\)