单纯形算法

单纯形算法

单纯形算法基于松弛形式进行操作：

\[\max z= \sum\limits_{j=1}^n c_j x_j \\ s.t. \begin{cases} x_{i+n}=b_i- \sum\limits_{j=1}^na_{ij}x_j,i=1,2,\dots,m \\ x_j \ge 0,j=1,2,\dots,n+m\end{cases} \]

其思路为：由于线性规划问题最优解一定可以在其可行域顶点处取得，所以先选一个初始点，之后不断尝试向相邻点去更新，如果更新不了就说明已经取得最优解了。

向相邻点更新的操作被称为转轴(Pivot)，而不断迭代更新的过程则被称为单纯形(Simplex)。

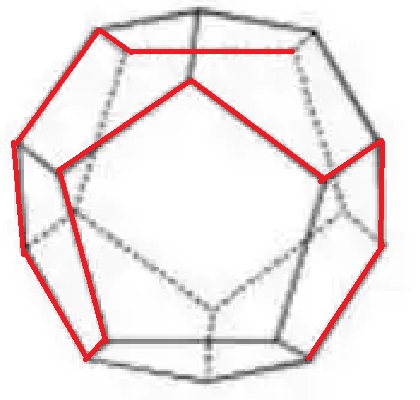
如图所示，红线显示了单纯形算法的流程。

因为凸集顶点个数有限，所以这个算法一定可以终止。

转轴

其作用为将一个非基变量和一个基变量交换。

形式为 \(Pivot(l,e)\)，表示将 \(x_{l+n}\) 与 \(x_e\) 交换，由定义得前者为非基变量，后者为基变量。

具体操作如下：

原式为 \(x_{l+n}=b_l- \sum\limits_{j=1}^na_{ij}x_j,i=1,2,\dots,m\)

把代 \(x_e\) 的一项移到等式左边，吧 \(x_{l+n}\) 移到等式右边，得 \(a_{ie}x_e=b_l-x_{l+n}- \sum\limits_{j=1}^n [j=e] a_{ij}x_j,i=1,2,\dots,m\)

把 \(a_{ie}\) 除到等式右边，得 \(x_e=\frac{b_l-x_{l+n}- \sum\limits_{j=1}^n [j=e] a_{ij}x_j,i=1,2,\dots,m}{a_{ie}}\)

用所得式替换原式，就实现了交换非基变量和基变量的操作。

单纯形

单纯形的思路为不断找到一组 \((l,e)\) ，然后执行 \(Pivot(l,e)\)。

具体操作为：

1. 找 \(e\)：找到一个满足 \(c_e \ge 0\) 的非基变量 \(x_e\)
2. 找 \(l\)：找到满足 \(a_{le}>0\) 且 \(\frac{b_l}{a_{le}}\) 最小（约束最紧）的基变量 \(x_{l+n}\)
3. 执行 \(Pivot(l,e)\)
4. 不断执行1~3步直至终止

终止的情况有 2 种：

1. 找不到一个 \(e\) 使得 \(c_e \ge 0\)，证明此时已经找到了最优解。
2. 找不到一个合法的 \(l\)，证明此时最优解为无穷大，即线性规划问题可行域无界。这种情况不在我们讨论范围内。

初始化

初始化需要一个辅助线性规划：

\[\max z= -x_0 \\ s.t. \begin{cases} x_{i+n}=b_i- \sum\limits_{j=1}^na_{ij}x_j+x_0,i=1,2,\dots,m \\ x_j \ge 0,j=0,1,2,\dots,n+m\end{cases} \]

如果原线性规划存在一个可行解 \((\hat{x}_{1},\hat{x}_{2},\dots,\hat{x}_{n+m})\)，则辅助线性规划必然存在一个可行解 \((0,\hat{x}_{1},\hat{x}_{2},\dots,\hat{x}_{n+m})\)。又因为 \(x_0\ge 0\)，所以该可行解为辅助线性规划的最优解。

之后只需要找到 \(l\) 使得 \(b_l\) 最小，然后执行 \(Pivot(l,0)\) 就得到了初始解。

时间复杂度分析

初始化的时间复杂度和单纯形的时间复杂度同阶，故只分析单纯形的时间复杂度。

不难理解一次 \(Pivot\) 的时间复杂度是 \(O(nm)\)，而影响时间复杂度的关键在于 \(Simplex\) 执行 \(Pivot\) 的次数。

该次数期望执行 \(m\) 次。但不幸的是，其最坏执行次数与凸集顶点个数同阶，即指数级。Klee–Minty cube 就是一个将单纯形算法卡到指数级的例子