[安乐椅#5] 一种利用二次曲线系证定点的方法

前置知识：二次曲线系

考虑二次曲线 \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) 只需要平面内 5 个点（任意 3 点不共线）即可唯一确定。所以如果用 4 个点进行限制，放开 1 个自由度，就能表示一类曲线。然后再与已知直线联立，就可以求得一些关系。

常见形式是：在 \(C_1\) 与 \(C_2\) 有 \(4\) 个不共线交点的情况下，\(\lambda C_1+ \mu C_2=0\) 能够表示所有过这 \(4\) 个交点的二次曲线。

这个 \(C_i\) 是某种二次曲线，如：圆、椭圆、双曲线、两根直线。

在实际操作时，常将二次曲线系与一已知二次曲线联立，即 \(\lambda C_1+ \mu C_2=C_3\)，来求解问题。

---

例一：拉尔瓦定理

已知抛物线 \(C:y^2=2px(p>0)\)，\(D(n,0),E(m,0)\) 为其对称轴上两点，\(M\) 是 \(C\) 上异于原点 \(O\) 的一动点，直线 \(ME\) 交 \(C\) 于 \(N\)，直线 \(MD\) 交 \(C\) 于 \(P\)，直线 \(ND\) 交 \(C\) 于 \(Q\)，直线 \(PQ\) 交 \(C\) 的对称轴于 \(G\)。

求证：\(G\) 为定点。

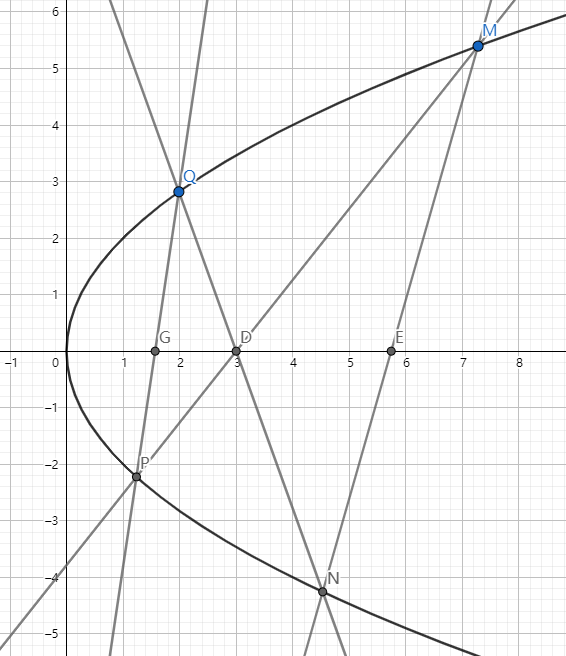
把 \(C,(l_{QN},l_{MP}),(l_{QP},l_{MN})\) 分别作为三个曲线系。即，利用 \(C,(l_{QN},l_{MP})\) 构造过 \(Q,N,P,N\) 四点的曲线系，然后将 \((l_{QP},l_{MN})\) 代入。

设 \(DP:x=k_1y+q,QN:x=k_2y+n,MP:x=k_3y+n,MN:x=k_4y+m\)。

方程为：\(\lambda(y^2+2px)+\mu(k_2y+n)(k_3y+n)=(k_1y+q)(k_4y+m)\)

解得：\(q=\dfrac{n^2}{m}\)。所以 \(G\) 为定点。

---

例二：手电筒模型

已知椭圆 \(C:x^2+2y^2+4x+4y=0\)，其上有一点 \(A(0,0)\)。\(M,N \in C\)，且 \(AM \perp AN,AD \perp MN,D\) 为垂足。求证：存在定点 \(Q\) 使得 \(|DQ|\) 为定值。

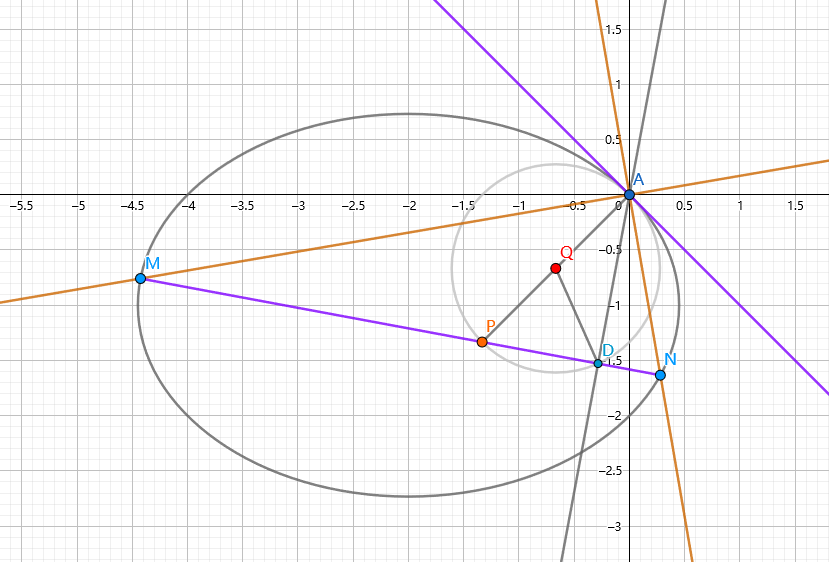
一种错误的分配的方法是 \(C,(l_{MN},\color\red{l_{AD}}),(l_{AM},l_{AN})\)。其错误原因是 \(C_3\) 只通过 \(C_1,C_2\) 4 个交点的其中 3 个，相当于放出了 2 个自由度，曲线系方程就解不出来了。

正确的分配方法是 \(C,(l_{MN},{l_{A}}),(l_{AM},l_{AN})\)，其中 \(l_A\) 表示 \(C\) 在 \(A\) 处的切线。虽然这样看上去 \(C_1,C_2\) 的交点只有 3 个，但实际上由于切线的存在，相当于有 2 个点共点，所以这个分配方法是满足切线系要求的。

先讨论一波 \(k_{MN}\) 不存在的情况，此处略。

设 \(AN:y=kx,AMy=\frac{-x}{k},MN:px+qy+1=0\)。

列出方程：\(\lambda(x^2+2y^2+4x+4y)+\mu(kx-y)(x+ky)=(x+y)(px+qy+1)\)。

解方程的时候没必要全拆开，可以按照不同项分别找系数对应相等，比如本题中：

\(x^2\) 项：\(\lambda+\mu k=p\)

\(y^2\) 项：\(2\lambda-\mu k=q\)

\(x\) 项：\(4\lambda=1\)

解得 \(p+q=\frac{3}{4}\)。故 \(l_{MN}\) 恒过 \(P(-\frac{4}{3},-\frac{4}{3})\)。

因为 \(A,P\) 为定点，\(AD \perp DP\)，所以 \(D\) 必在以 \(AP\) 为直径的圆上运动。故存在定点 \(Q\) 为 \(AP\) 中点即 \(Q(-\frac{2}{3},-\frac{2}{3})\)。