浅谈几种解决最短路问题的算法
目录
一. 图的相关概念
二. 最短路问题的内容与实际应用
三. 解决单源最短路的 2 种算法
0. 松弛操作
1. Bellman-Ford 算法及 SPFA 算法
1.1 Bellman-Ford 算法
1.2 SPFA 算法
2. Dijkstra 算法
四. 解决全源最短路的 2 种算法
1. Floyd 算法
2. Johnson 算法
2.0 有关全源最短路与单源最短路的思考
2.1 一种错误的尝试
2.2 由尝试启发出的正解
五. 参考资料
一. 图的相关概念
图 (Graph) 定义为一个二元组 \(G=(V(G),E(G))\)。其中 \(V(G)\) 是非空集,称为 点集 (Vertex set),对于 \(V(G)\) 中的每个元素,称其为 顶点 (Vertex) 或 节点 (Node),简称 点;\(E(G)\) 为 \(V(G)\) 各结点之间 边 的集合,称为 边集 (Edge set)。
若 \(E(G)\) 中每一条边为一个无序二元组 \((u,v)\),一般记作 \(u \leftrightarrow v\),称为 无向边(Undirected edge),其中 \(u,v \in V(G)\)。设 \(e=u \leftrightarrow v\),则 \(u,v\) 称为 \(e\) 的 端点(Endpoint),也简称 点。此时 \(G\) 称为 无向图(Undirected graph)。
若 \(E(G)\) 中每一条边为一个有序二元组 \((u,v)\),一般记作 \(u \to v\),称为 有向边(Directed edge),其中 \(u,v \in V(G)\)。设 \(e=u \to v\),则 \(u\) 称为 \(e\) 的 起点(Tail),\(v\) 称为 \(e\) 的 终点(Head)。此时 \(G\) 称为 无向图(Undirected graph)。
若 \(G\) 的每一条边 \(e_k=(u_k,v_k)\) 均被赋权,则称 \(G\) 为 赋权图。若这些权均为正实数,则称 \(G\) 为 正权图。一般来讲,如果 \(G\) 没有被赋权,则默认边权为 \(1\)。
在无向图 \(G=(V,E)\) 中,若存在 \(e=(u,v) \in E\),则称 \(u\) 和 \(v\) 相邻(Adjacent) 或 相连(Incident)。
定义一个点 \(u\) 的 邻域(Neighborhood) 为所有与 \(u\) 相连的点构成的集合,记作 \(N(u)\)。
途径(Walk) 是边的有序子集,记其为 \(W=\{(P_1,P_2),(P_2,P_3),(P_3,P_4),...,(P_{k-1},P_k)\}\),即其必须满足第一条边的终点是第二条边的起点,最后一条边的起点是倒数第二条边的终点,除此之外的边的起点是上一条边的终点,终点是上一条边的起点。
路径(Path) 是边集中的点各不相同的途径。从 \(s\) 到 \(t\) 的路径一般记作 \(s \rightsquigarrow t\)。
对于点 \(u,v \in V\),若存在一条途径使得 \(P_1=u,P_k=v\),则称 \(u\) 和 \(v\) 连通(Connected)。
若 \(G\) 的任意两点都连通,则称 \(G\) 是一个 连通图(Connected graph)。
二. 最短路问题的内容与实际应用
最短路问题(Short-path problem) 的基本模型为:在一张赋权图上,给定若干组源点和汇点,欲求出各组源汇点之间边权和最小的路径。
虽然最短路可能有很多条,但是其值是唯一的。
单源最短路问题 即固定一个源点 \(s\),求所有汇点 \(t \in \mathbb{N_+}\) 求最短路的问题。
全源最短路问题 即对于所有源点 \(s \in \mathbb{N_+}\),求所有汇点 \(t \in \mathbb{N_+}\) 求最短路的问题。
最短路问题在生活实际中应用广泛,比如铺设电缆、管道等怎样能使开销最小,医院等公共设施建设在哪里能使的其离周围各个社区的距离相对较近。
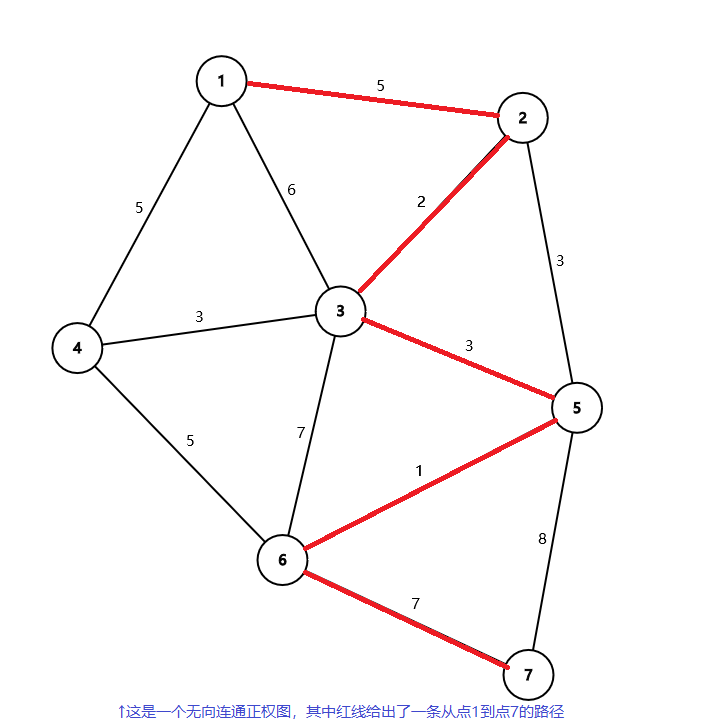
三. 解决单源最短路的 2 种算法
0. 松弛操作
以下记 \(d_u\) 表示从 \(s\) 到 \(u\) 的最短路,\(w_{u,v}\) 表示边 \((u,v)\) 的边权。图的点数为 \(n\),图的边数为 \(m\)。
最短路都基于 松弛操作,因此先放在介绍最短路算法之前加以说明。
对于边 \((u,v)\),其松弛操作为 \(d_v=\min(d_v,d_u+w_{u,v}),u \in N(v)\)。即我们尝试从 \(s \rightsquigarrow u \to v\) 这样走能否成为比当前存下的 \(d_v\) 更短的“更短路”,如果是则更新 \(d_v\)。
1. Bellman-Ford 算法及 SPFA 算法
1.1 Bellman-Ford 算法
Bellman-Ford(简称 BF)的思路非常直接,即不断对图上每一条边进行松弛操作,不断循环尝试松弛直至某次循环中没有可以松弛的边为止。
算法正确性是显然的,因为我们已经把能松弛的边都尽可能松弛了。
由于每次循环都会使最短路长度至少 \(+1\),而最短路长度至多是 \(n-1\),故循环至多执行 \(n-1\) 次。而每次循环松弛 \(m\) 条边,故 BF 的时间复杂度为 \(\mathcal O(nm)\)。
1.2 SPFA 算法
在 BF 进行松弛时,有大量无效的节点也被考虑在内了,因此 BF 的效率十分低下,而一系列的优化也随之而来,其中最著名的就是 SPFA 算法。
SPFA(Shortest Path Faster Algorithm) 是“队列优化的 BF 算法”,这也是国际上对它的通用称呼。国内一般称其为 SPFA,这是其发明者段凡丁 1994 年在其论文中的称呼。其优化思想为:只有刚刚松弛完的节点才可能继续松弛其它节点。
考虑使用队列维护刚刚松弛完的节点。一开始我们将源点 \(s\) 入队并标记入队标记 \(vis\)。之后每一次松弛,我们取出队首 \(u\),将其的 \(vis\) 去除。然后让 \(u\) 尝试去松弛其邻域内的节点。如果松弛成功,若该节点不在队列中,则将该节点入队并标记 \(vis\)。直至队列为空就结束了。
SPFA 算法期望时间复杂度为 \(\mathcal{O}(kn)\),其中 \(k \approx 2\)。但是其最高时间复杂度仍为 \(\mathcal{O}(nm)\),同 BF 一样。
部分网格图和蒲公英图可以使 SPFA 的复杂度趋向最高。
- SPFA 的代码实现(c++):
void init(){
while(!q.empty()) q.pop();//清空队列
memset(d,0x3f,sizeof(d));//最短路初值设为无穷大
memset(vis,0,sizeof(vis));//入队标记初值为空
}
void spfa(long long st){
long long i,u,v;
init();
q.push(s); vis[s]=1; d[s]=0;//将源点入队并标记,源点最短路初始化为0(自己到自己的距离为0)
while(!q.empty()){//一直松弛直至队列为空
u=q.front(); q.pop(); vis[u]=0;//取出队首并去除标记
for(i=h[u];i;i=e[i].nxt){//尝试松弛
v=e[i].v;
if(d[v]>d[u]+e[i].w){
d[v]=d[u]+e[i].w;//松弛成功
if(!vis[v]){
q.push(v); vis[v]=1;//入队并标记
}
}
}
}
}
2. Dijkstra 算法
Dijkstra 算法由荷兰计算机科学家 Dijkstra 于 1959 年发表。其只适用于正权图。
Dijkstra 运用著名思想:蓝白点思想。即一开始所有节点均为白色,将松弛完全的节点染成蓝色,之后不再考虑这些蓝点。
初始化 \(d_s=0,d_u=INF,u \ne s\)。
之后进行 \(n\) 次循环,每次找出当前所有白点中 \(d\) 最小的一个,让它去松弛其邻域内的节点。然后把它染成蓝色。
正确性证明可以用归纳法。我们假定所有蓝点的最短路值都已正确(松弛完全)。显然在蓝点只有 \(s\) 时正确。每次循环找到最短路最小的白点,因为所有边权为正,其无法被其它白点所松弛,而蓝点又已松弛完全,所以此时它也松弛完全,可以染成蓝色并松弛其邻域节点。正确性证毕。
如果每次循环暴力寻找白点最短路最小值,则算法时间复杂度显然为 \(\mathcal{O}(n^2)\)。如果将所有节点压入优先队列中,每次查询队头,则可以将时间复杂度降至 \(\mathcal{O}(m \log m)\)。如果使用二叉堆或者斐波那契堆维护可以降至 \(\mathcal{O}(m \log n)\)。可以根据实际情况估计 \(m\) 与 \(n^2\) 的关系决定使用哪种方式维护。
- 优先队列优化 Dijkstra 的代码实现(c++):
struct node{
long long w,id;
bool operator <(const node &x)const {return x.w<w;}
};priority_queue <node> q;//重载优先队列
memset(vis,0,sizoef(vis));//初始化均为白点
memset(d,0x3f,sizeof(d)); d[s]=0;//初始化除s外d均为正无穷
q.push(node{d[s],s});//将源点入队
while(!q.empty()){
node uu=q.top();u=uu.num;q.pop();//取出d最小的点
if(vis[u]) continue;//如果是蓝点就不管
vis[u]=1;//是白点,将其染蓝
for(i=h[u];i;i=e[i].next){
v=e[i].to;
if(d[v]>d[u]+e[i].w){//松弛
d[v]=d[u]+e[i].w;
q.push(node{d[v],v});
}
}
}
四. 解决全源最短路的 2 种算法
以下记 \(d_{u,v}\) 表示从节点 \(u\) 到节点 \(v\) 的最短路长度。\(n,m\) 同上。
1. Floyd 算法
Floyd 运用动态规划的思想。
记 \(a_{u,v}\) 表示边 \(u \to v\) 的边权,若 \(u\) 和 \(v\) 之间没有边则边权为正无穷;记 \(d_{k,u,v}\) 表示从节点 \(u\) 到节点 \(v\) 只经过节点编号小于等于 \(k\) 进行转移的节点的最小值。
初始化 \(d_{1,u,v}=a_{u,v}\)。
显然有转移方程:\(d_{k,u,v}=\min(d_{k-1,i,j},d_{k-1,i,k}+d_{k-1,k,j}),k>1\)。
由于方程的第一维只由 \(k-1\) 转移到 \(k\),所以可以使用滚动数组优化掉第一维:\(d_{i,j}=\min(d_{i,j},d_{i,k}+d_{k,j}),k>1\)。
正确性是显然的。因为其枚举了所有可能作为松弛转移的节点,每次循环只会增加一个新的可能松弛点。
时间复杂度显然为 \(\mathcal{O}(n^3)\)。
- Floyd 的代码实现(c++):
memset(d,0x3f,sizeof(d));//初始权值设为无穷大
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(a[i][j]) d[i][j]=a[i][j];//录入初始边
for(i=1;i<=n;i++) d[i][i]=0;//自己到自己是0
for(k=1;k<=n;k++)//最外层必须枚举k,因为Floyd成立的前提就是只经过1~k号节点松弛且该次松弛完全
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);//松弛操作
2. Johnson 算法
2.0 有关全源最短路与单源最短路的思考
全源最短路显然可以通过 \(n\) 次单源最短路解决。
法一:如果进行 \(n\) 次 SPFA,那最坏情况下时间复杂度是 \(\mathcal{O}(n^2m)\) 的,甚至比 Floyd 还慢。
法二:如果进行 \(n\) 次 Dijkstra(这里用最常见的优先队列优化 Dijkstra),时间复杂度是 \(\mathcal{O}(nm \log m)\) 的,在 \(m\) 相较于 \(n^2\) 很小时表现优异。但是由于 Dijkstra 本身的限制,这种做法只能用于正权图。
能否存在一种可以在任意图上使用的 \(\mathcal{O}(nm \log m)\) 的多源最短路算法呢?
2.1 一种错误的尝试
一种明显的尝试是:能否通过让所有边均加上一个常数,使得所有边都成为正边,然后使用上述法二呢?
很不幸,这是错误的。见下图:
在原图中,最短路为右侧路径。但将边权全部 \(+5\) 后最短路成为了左侧路径。这是由于每条路径所经过的边数是不同的,强制给每条边加上一个相同的值会使得给所有的路径加上一个不同的值。所以这种尝试是错误的。
2.2 由尝试启发出的正解
尝试启发我们给每一条边重新赋成正权,但又不能影响路径间的相对大小。Johnson 为解决这个问题而生。
Johnson 的重新赋权的方法为:新建一个超级源点 \(S\),将 \(S\) 向各节点连一条边权为 \(0\) 的有想边。然后用 BF 或者 SPFA(Johnson 提出者使用的是 BF,因为当时还没有 SPFA。不过这不是复杂度瓶颈)求以 \(S\) 为源点的单源最短路,记作 \(h_u\)。接下来对于每一条权为 \(w\) 的边 \(u \to v\),将其边权重赋为 \(h_u+w-h_v\)。最后使用上述法二即可求出全源最短路。
要证明其正确性,只需证明 \(2\) 点:边权重赋值后为正、路径间相对大小关系不会影响最短路的确定。
根据松弛操作,对于一条权为 \(w\) 的边 \(e=u\to v\),其满足 \(h_u+w \ge h_v\),否则松弛操作会一直进行下去。所以重新赋权后边权为正。
对于一条路径 \(s \rightsquigarrow t = \{e_1=(s,p_2),e_2=(p_2,p_3),e_3=(p_3,p_4)...,e_{k-1}=(p_{k-1},t)\}\),其原长:
\(W=e_{w_1}+e_{w_2}+e_{w_3}+...+e_{w_{k-1}}\)
重新赋权后 :
\(W'=(e_{w_1}+h_s-h_2)+(e_{w_2}+h_2-h_3)+(e_{w_3}+h_3-h_4)+...+(e_k-1+h_{k-1}-h_t)\)
化简得:
\(W'=e_{w_1}+e_{w_2}+e_{w_3}+...+e_{w_{k-1}}+h_s-h_t=W+h_s-h_t\)
由上式得,重新赋权后的路径长度只与 \(W,h_s,h_t\) 有关,没有改变路径长度的相对大小关系。
正确性证毕。
BF 或者 SPFA 的复杂度是 \(\mathcal{O}(nm)\),进行 \(n\) 次 Dijkstra 的时间复杂度是 \(\mathcal{O}(nm \log m)\)。复杂度瓶颈在后者。故 Johnson 的时间复杂度是 \(\mathcal{O}(nm \log m)\)。
- Johnson 的代码实现(c++):
n++;s=n;
for(i=1;i<n;i++) add(s,i,0);//新建超级源并连边
for(i=1;i<=n;i++) H[i]=1e9;//SPFA
q.push(s); H[s]=0; vis[s]=1;
while(!q.empty()){
u=q.front(); q.pop(); vis[u]=0;
for(i=h[u];i;i=e[i].nxt){
v=e[i].v; w=e[i].w;
if(H[v]>H[u]+w){
H[v]=H[u]+w;
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
}
n--;//去除超级源
for(u=1;u<=n;u++){//重新赋权
for(i=h[u];i;i=e[i].nxt){
v=e[i].v;
e[i].w=e[i].w+H[u]-H[v];
}
}
for(s=1;s<=n;s++){//Dijkstra
ans=0;
for(i=1;i<=n;i++) d[i]=1000000000000;
memset(vis,0,sizeof(vis));
while(!pq.empty()) pq.pop();
d[s]=0; pq.push((node){d[s],s});
while(!pq.empty()){
node gx=pq.top(); pq.pop();
u=gx.id;
if(vis[u]) continue;
vis[u]=1;
for(i=h[u];i;i=e[i].nxt){
v=e[i].v; w=e[i].w;
if(d[v]>d[u]+w){
d[v]=d[u]+w;
pq.push((node){d[v],v});
}
}
}
for(i=1;i<=n;i++) d[i]=d[i]-H[s]+H[i];//还原最短路的初始值
for(i=1;i<=n;i++) if(d[i]>=1e9) d[i]=1e9;//不连通即为无穷大
for(i=1;i<=n;i++) printf("%lld ",d[i]);
printf("\n");
}
五. 参考资料
- OI-wiki:《图论相关概念》https://oiwiki.com/graph/concept/
- OI-wiki:《最短路》https://oiwiki.com/graph/shortest-path/



