[安乐椅#2] 抛物线准线梯形

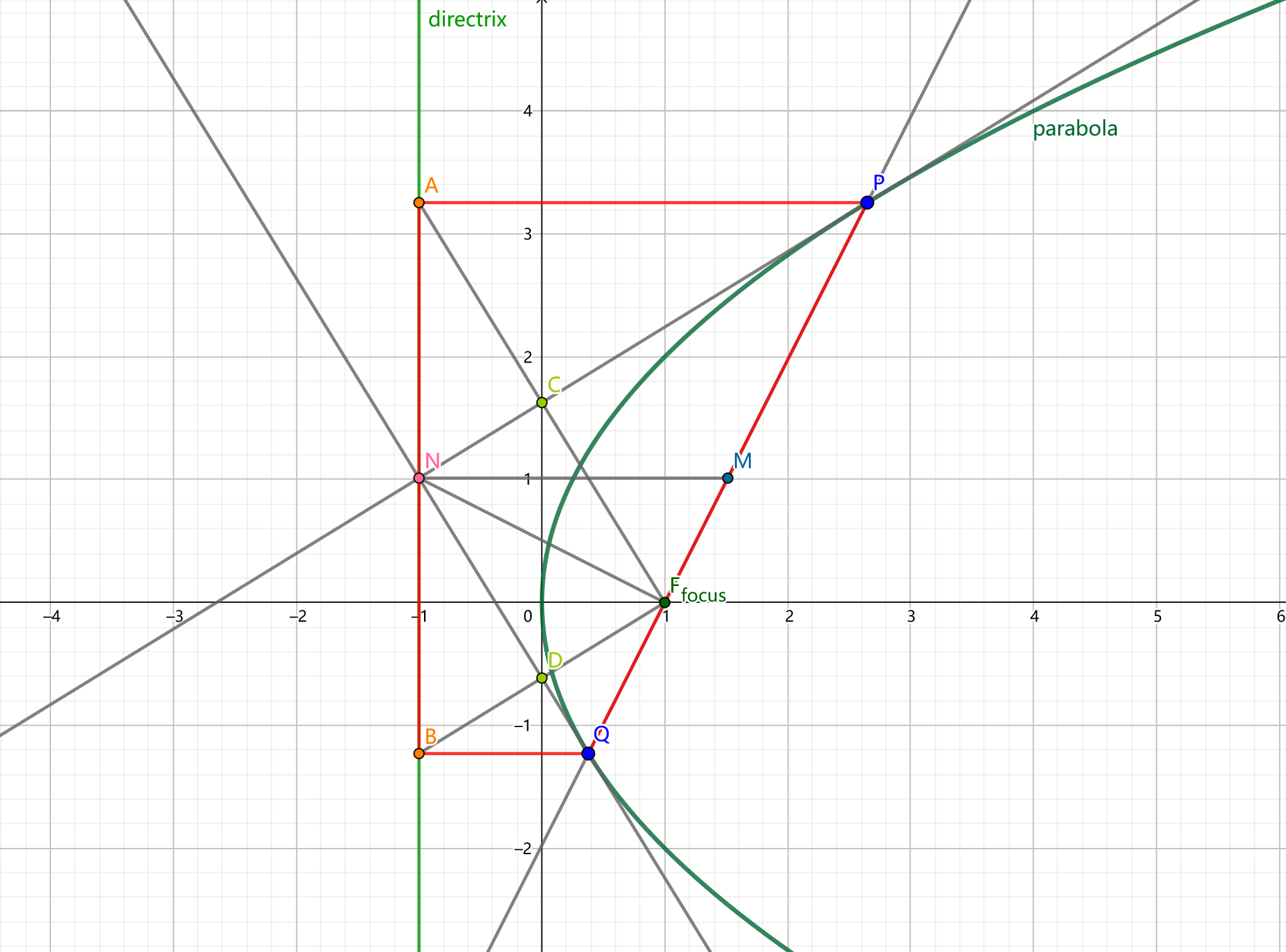
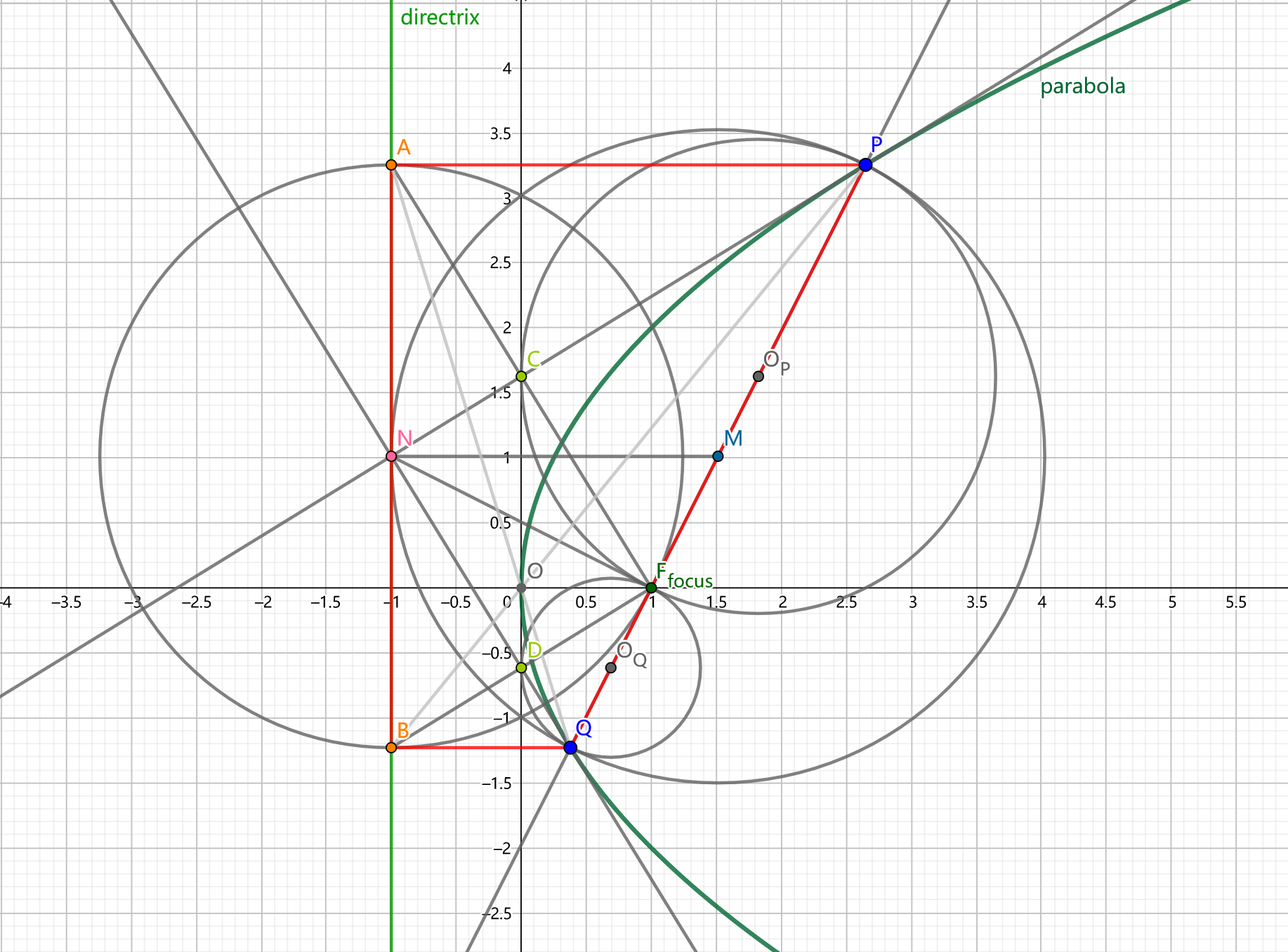
如图，对于抛物线 \(\Gamma:y=2px(p>0)\)，\(F(\frac{x}{2},0)\) 为其焦点，\(\delta:x=-\frac{x}{2}\) 为其准线。一过 \(F\) 的直线交 \(\Gamma\) 于 \(P,Q\) 两点。过 \(P,Q\) 两点分别向 \(\delta\) 作垂，垂足分别为 \(A,B\)。过 \(P,Q\) 两点分别做 \(\Gamma\) 的切线，交 \(y\) 轴分别于 \(C,D\)。\(M\) 为 \(P,Q\) 中点。

则有：

1. \(C\) 为 \(AF\) 中点，直线 \(CP\) 垂直平分 \(AF\)。\(D\) 为 \(BF\) 中点，直线 \(DQ\) 垂直平分 \(BF\)。

2. 直线 \(PC,QD\) 交 \(\delta\) 于同一点 \(N\)。

3. \(AP \space /\kern -0.8em / \space BQ \space /\kern -0.8em / \space NM\)。

4. \(\angle PNQ=\angle AFB=\angle PCF=\angle QDF=90^\circ\)。

5. \(A,O,Q\) 三点共线，\(B,O,P\) 三点共线。