[安乐椅#7] 二元抛物面反射光

问题描述：已知二元抛物面 \(P:4Fz=x^2 + y^2\)，焦点点光源 \(Fo(0,0,F)\)，反射点 \(Li(a,b,c)\)，求反射光线。

---

前置知识：二元函数切面

若二元函数 \(z=f(x,y)\) 在 \((x_0,y_0)\) 处可微，记 \(z_0=f(x_0,y_0)\)，则其在 \((x_0,y_0)\) 处的切面为：

\[z-z_0=[f^\prime_x(x_0,y_0)](x-x_0)+[f^\prime_y(x_0,y_0)](y-y_0) \]

---

前置知识：平面法向量

平面 \(Ax+By+Cz+D=0\) 的一个法向量为 \((A,B,C)\)。

---

光的反射定理在曲面中仍然适用：反射光、入射光、法线位于同一平面；反射光和入射光分居法线两侧；反射角等于入射角。

---

目前仅做到利用GGb画出出射光线的程度。

首先，利用二元函数切面公式，求出 Li 关于 P 的切面。然后去求法平面。

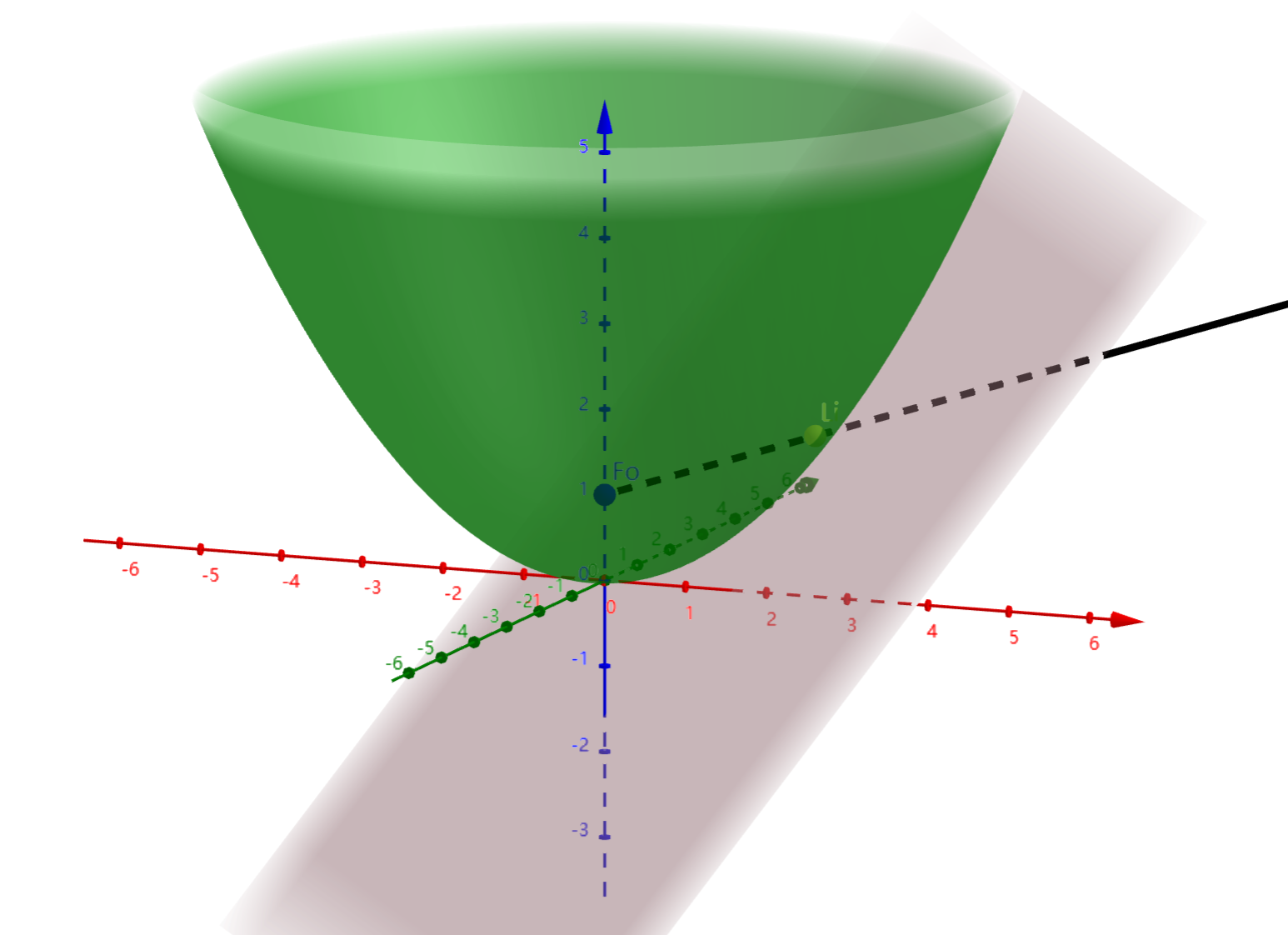
考虑求这个法平面的条件是：过已知直线Fo-Li，且与切面垂直。这个直接解析很麻烦，我们不妨利用GGb的功能偷个懒（

过直线Fo-Li，可以转化为过Fo,Li这两个点。而与切面垂直，就是与其法向量平行，但是介于二元抛物面的顶点在原点，所以其实这个条件可以转化为过法向量对应的那个点。

人里：过三点的平面如何求？

九江：三点的坐标都可求，我会设法平面为Ax+By+Cz+D=0解方程！

人里：很好，你无了。

原因我还没想明白，但是如果硬用那三个点去解方程的话，会发现缺一个条件。大概会解出来ab和F的关系，但想解ABCD就会缺一个方程，不知道是不是不独立的问题。/fad

八苏：但是GGb有三点平面工具呀DA✩ZE

正确的。

我偷了个懒，直接用三点平面就把法平面搞出来了。

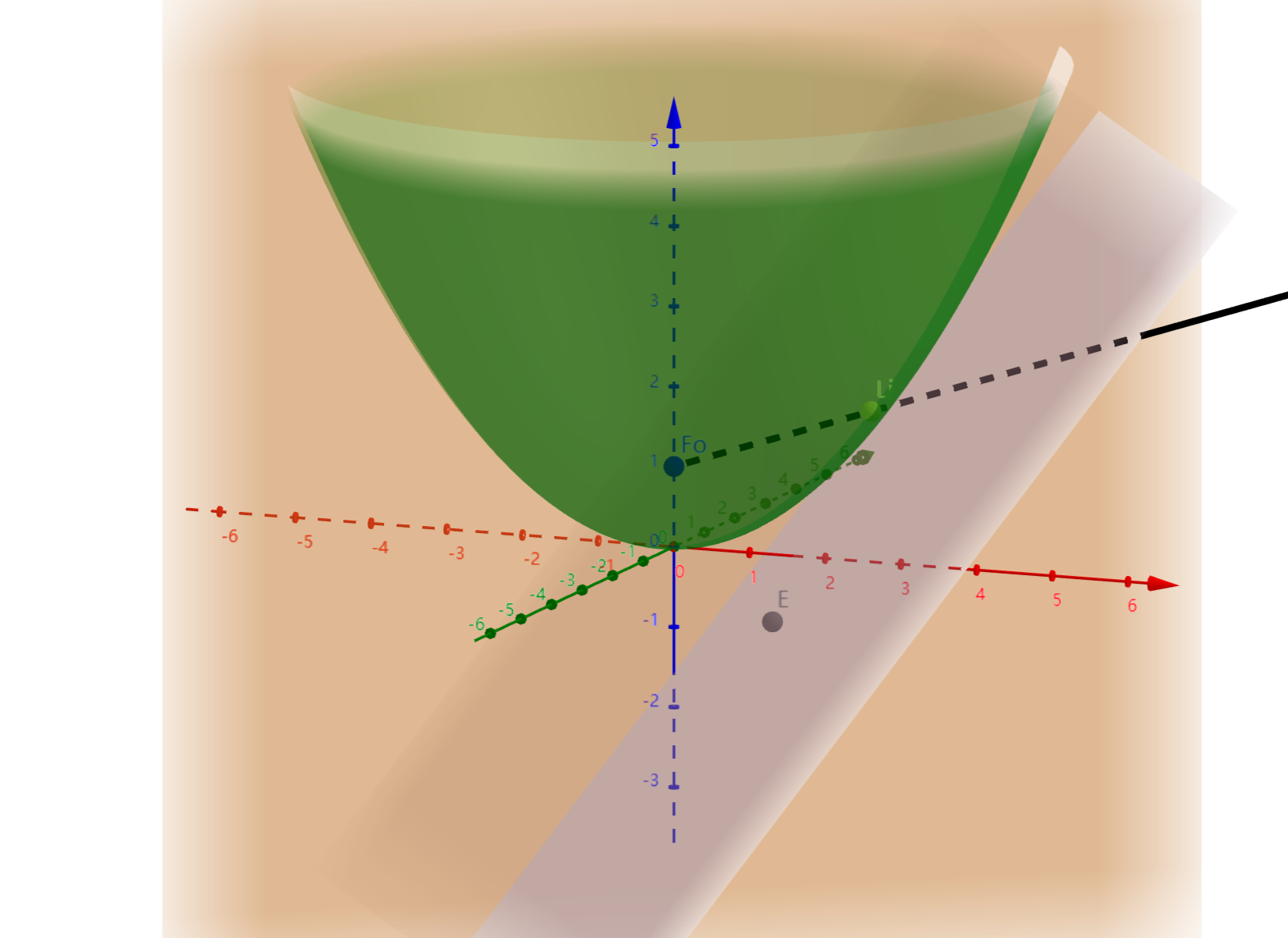
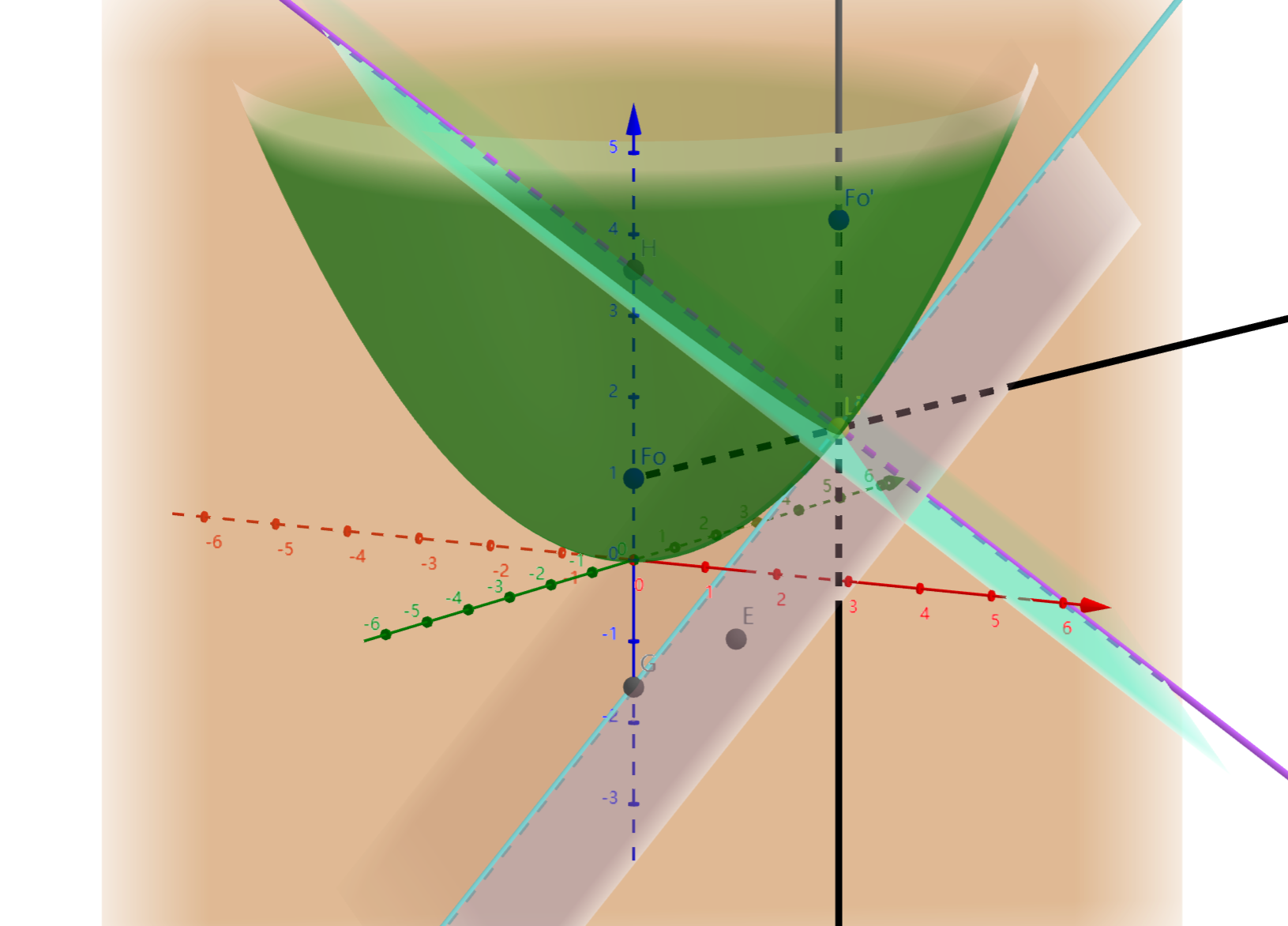
有了法平面，求法线就好说了。之后再做一个对称就赢了。

具体的细节可以参考对应的GGb文件：