[安乐椅#8] 依神效应

对于一个使用理想光源（均匀向四周发射光线的光源）、以二元抛物面为反射面的手电筒，在忽略其余光学原件对光路产生的影响的情况下，当光源低于焦点一定距离时，会在出射光边缘形成一个亮光圈。

（注：图中光圈的成因不是依神效应，但其现象是类似的）

出现这个效应的原理是：在抛物面内多次反射次数越多的光越趋向于在抛物面边缘射出。

便于研究起见，我们利用过z轴的平面去截抛物面，得到截线为抛物线，从而将立体问题转化为平面问题。

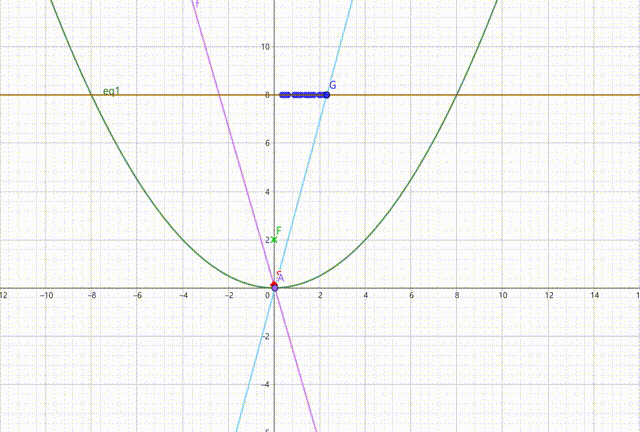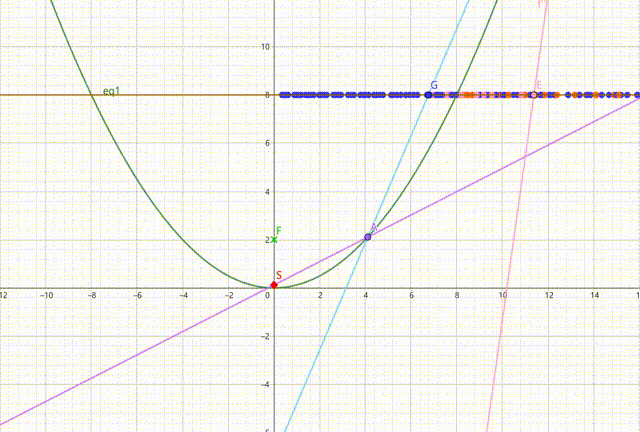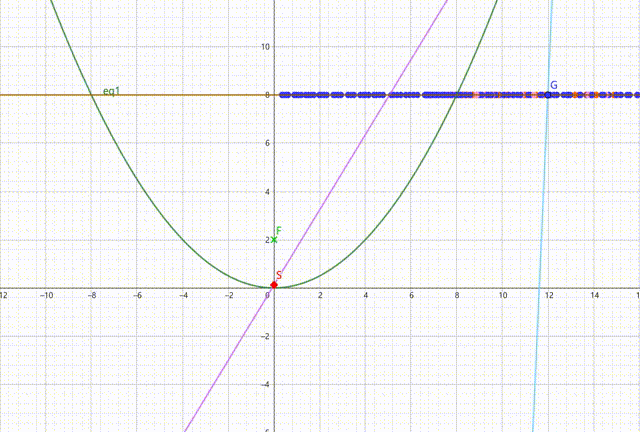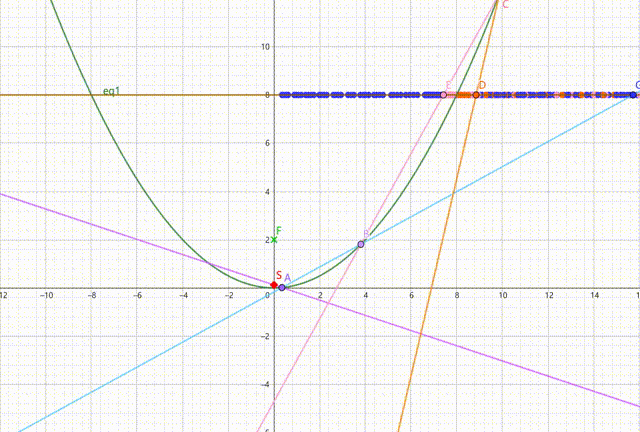
下图中，黄线以下部分为手电筒反射面，而紫、蓝、粉、橙色直线（应该用射线，但用直线表示便于作画）依次表示入射光、第一反射光、第二反射光、第三反射光。随入射光出射角变化，作出三条反射光线与黄线的交点的轨迹（仅作出对称轴右侧部分，左侧是对称的）。可以发现，在抛物线内部的部分，第一反射光交点轨迹全部占满黄线，第二反射光交点仅占黄线右侧一小部分，第三反射光交点占黄线右侧更小的一部分。

由此可见，介于入射光未经反射即出射的光基本是均匀的，一个点的光照强度在理想条件下主要取决于过这个点的光的条数。而靠近边缘的部分经过的光的条数要多于中间部分，故会形成一个亮圈。

下面浅要解释一下这个现象的原因。

为了便于解释，以下命题的成立均需要一个共同的前提条件：第一反射点（A点）的纵坐标高于出射点（S点）。虽然A点低于S点在一般手电筒内均成立，但讨论麻烦，故不做说明。

同时，仅考虑对称轴右侧光线。左侧光线是完全对称的。

---

结论1：对于一个反射点，其反射光线斜率大于入射光线斜率。

证明：设抛物线为\(2py=x^2\)，反射点为\(N(a,\frac{a^2}{2p})\)，入射光线斜率为 \(k_1\)，反射光斜率为 \(k_2\).

通过求导，不难得出\(N\)点处的切线斜率 \(k_0=\frac{a}{p}\)。

由于抛物线右侧是下凸增的，所以 \(k_0>k_1\).

根据到角公式，有 \(\frac{k_2-k_0}{1+k_2k_0}=\frac{k_0-k_1}{1+k_1k_0}\)

解得 \(k_2=\frac{k_1k_0^2-k_1+2k_0}{1+k_0^2}\).

下面比较 \(k_1\) 与 \(k_2\) 的大小，利用作差法，得：

\(\frac{k_1k_0^2-k_1+2k_0}{1+k_0^2}-k_1=\frac{2(k_0-k_1)}{1+k_0^2}\)

\(\because k_0>k_1\)

\(\therefore 上式>0\)

\(即，k_2>k_1\).

\(\Box\)

---

因为第一条入射光的斜率是正的，结论1证明了光线的斜率在一次反射中会变大，从而归纳地证明了光线的斜率一直是正的而且会越来越大。

这点非常重要，它说明了光即使在反射，也会“顺着”抛物线的图象走，而不会在抛物线的两端“乱跑”的行为。

---

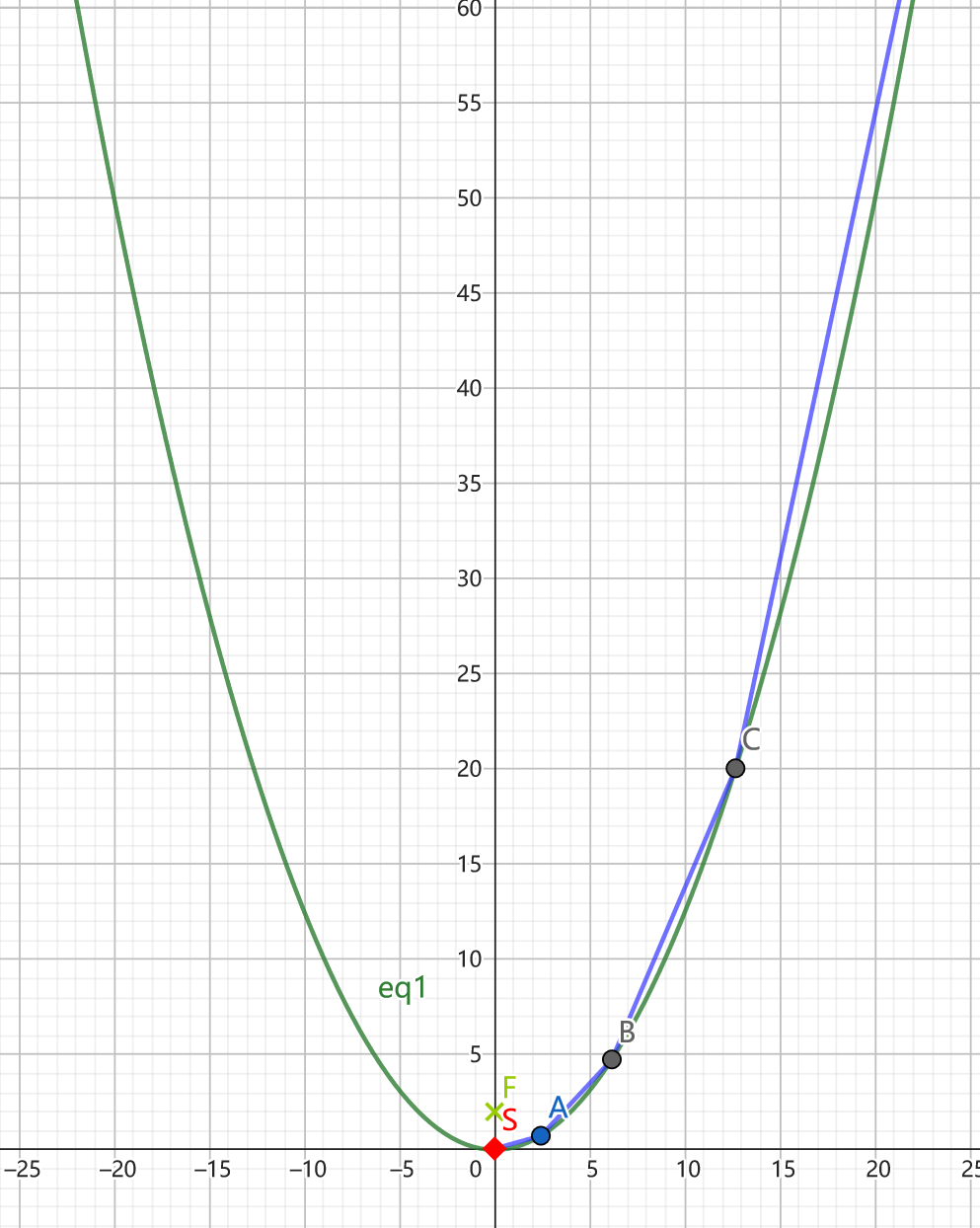
结论2：任何光在手电筒内的反射次数都是有限的。

结论1说明了光线会沿手电筒反射壁上升，直至射出手电筒。如果存在无限反射的情况，那只能是收敛。这点以我的能力暂时还无法严谨证明，但是根据抛物线的相似性，假如存在某束光线是收敛的，那必然对于任意抛物线都会存在这一束光线。但是，根据开头给出的例子，对于 \(8y=x^2\) 是不存在这束光线的，从而说明不存在这束光线。

---

根据结论2，任意光线最终都会射出手电筒。而根据结论1，光线反射越多次，其就越偏向于在手电筒边缘射出。如果简单地将光线条数作为亮度的主要衡量标准，就会出现该效应。