牛顿迭代法
牛顿迭代法
该算法的目标为：对于在 \([a,b]\) 上连续且单调的函数 \(f(x)\)，求方程 \(f(x)=0\) 的近似解。
算法流程
给定 \(f(x)\)。
初始时由一个相对近似零点 \(x_0\) 开始，不断迭代优化。
假设当前近似解为 \(x_i\)，作过点 \((x_i,f(x,i))\) 关于 \(f(x)\) 的切线，交 \(x\) 轴于 \((x_{i+1},0)\)，即认为 \(x_{i+1}\) 是一个更近似的解。不断重复该迭代过程。根据导数的性质，有：
\[f'(x_i)=\dfrac{f(x_i)}{x_i-x_{i+1}}
\]
整理得核心递推式：
\[x_{i+1}=x_i-\dfrac{f(x_i)}{f'(x_i)}
\]
在一定条件下，随着迭代次数的增加，\(x_i\) 会越来越逼近 \(f(x)=0\) 的解。
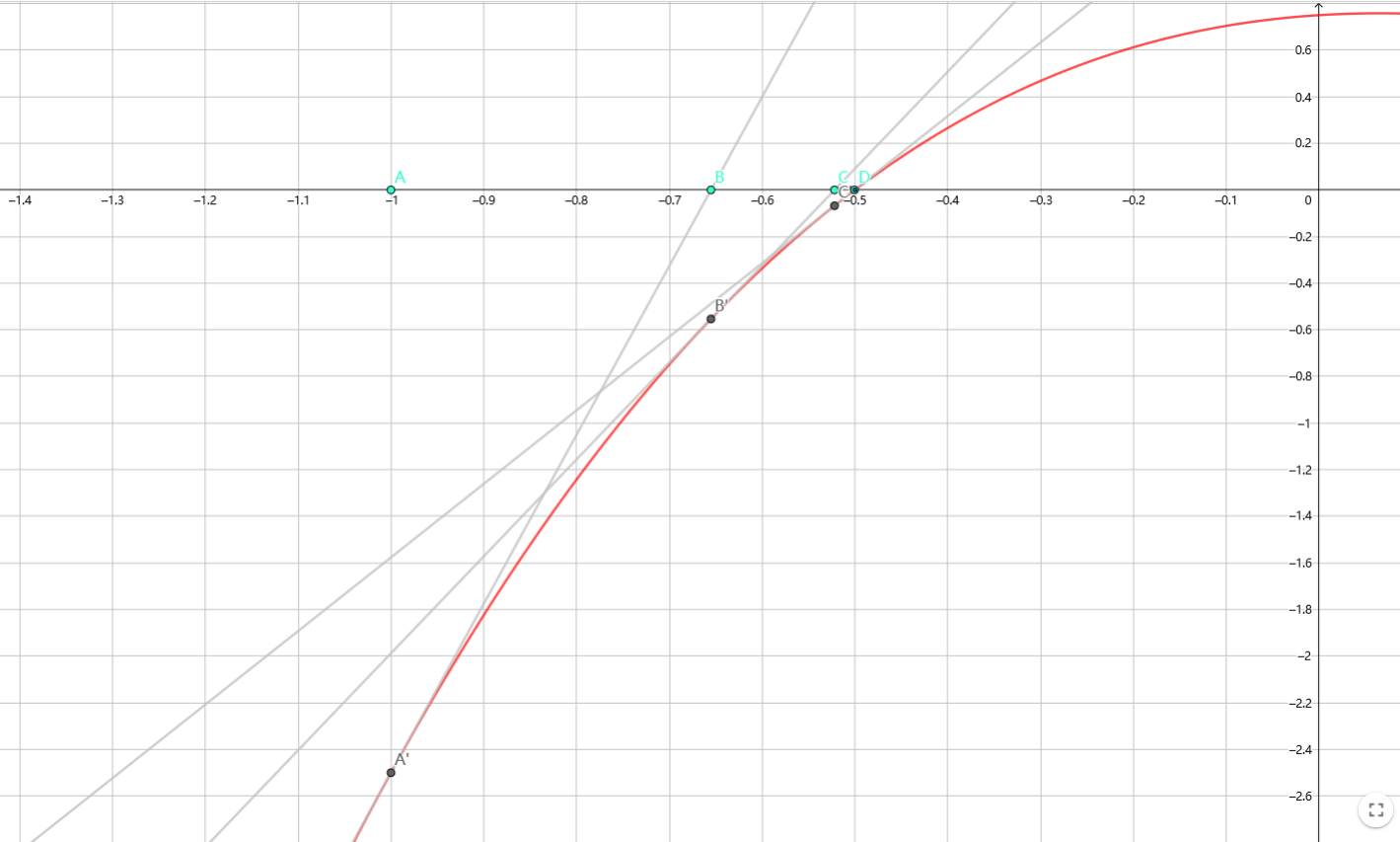
收敛性
可以证明，牛顿迭代法的收敛性时平方极的。相对而言还是比较优异的。
局限性
-
对于一个的 \(x_0\)，最后只能找到一个根近似值。但如果 \(f(x)=0\) 有多解，则牛顿迭代法无法保证能找到全部解。
-
在拐点或局部最大最小值附近可能发生振荡或发散。（图中 \(f(x)=5x^4-5x^3-5x^2+5x+\dfrac{1}{2}\)）
-
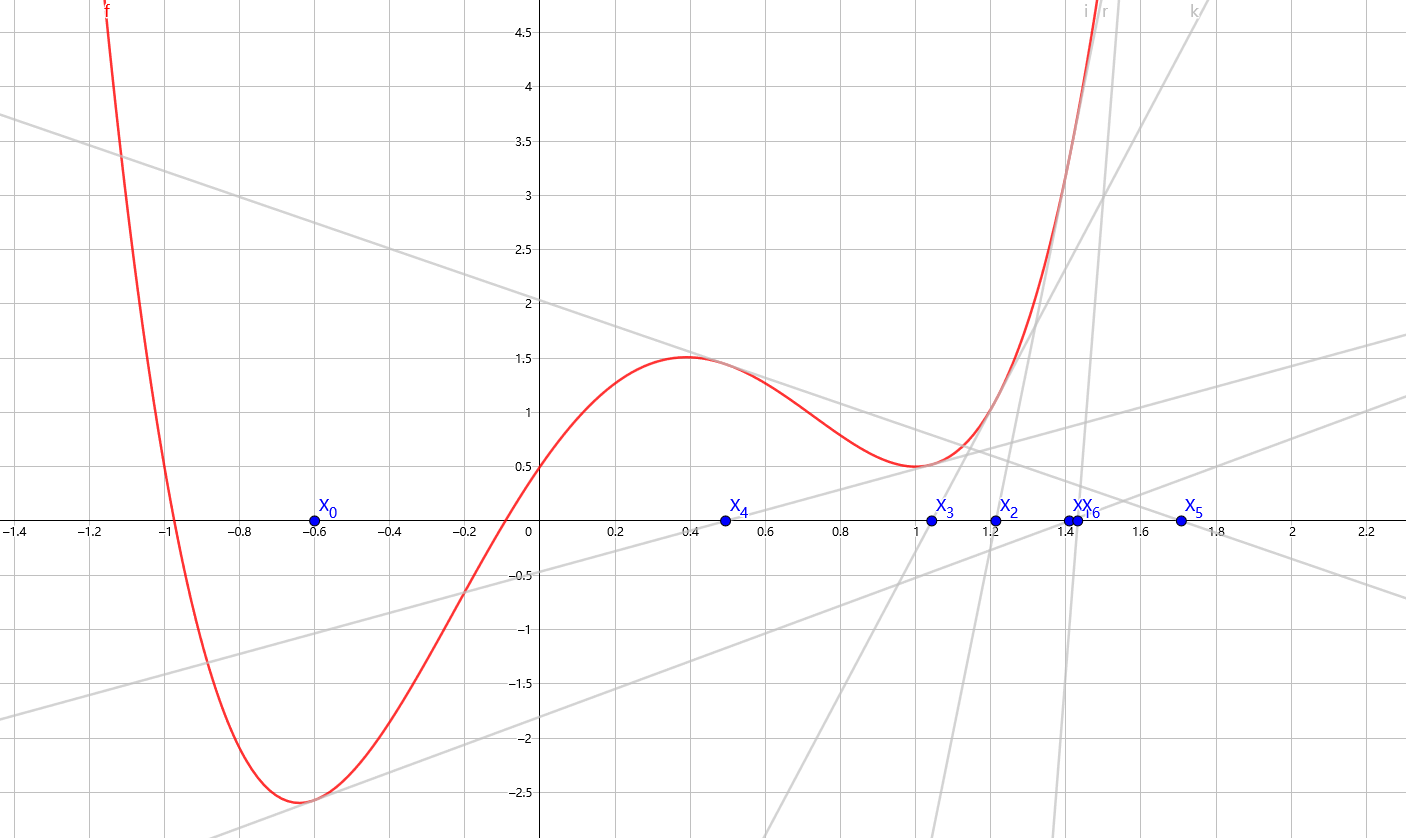
如果 \(f(x)\) 不收敛，那么有可能越迭代越远离零点。（图中 \(f(x)=x^{\frac{1}{3}}\)）
-
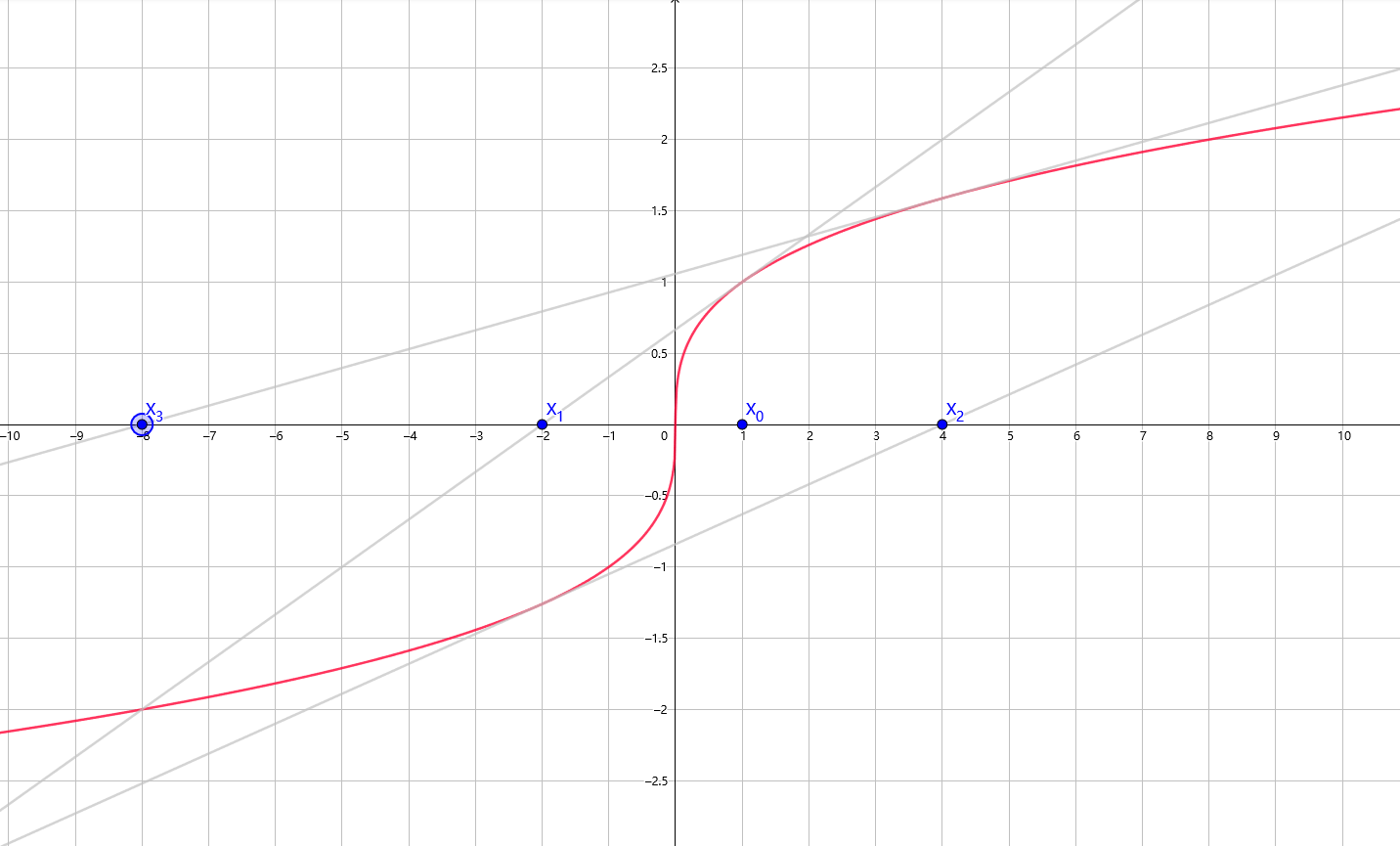
特殊 \(f(x)\) 导致循环震荡。（图中 \(f(x)=\sqrt{|x|}\)）
-
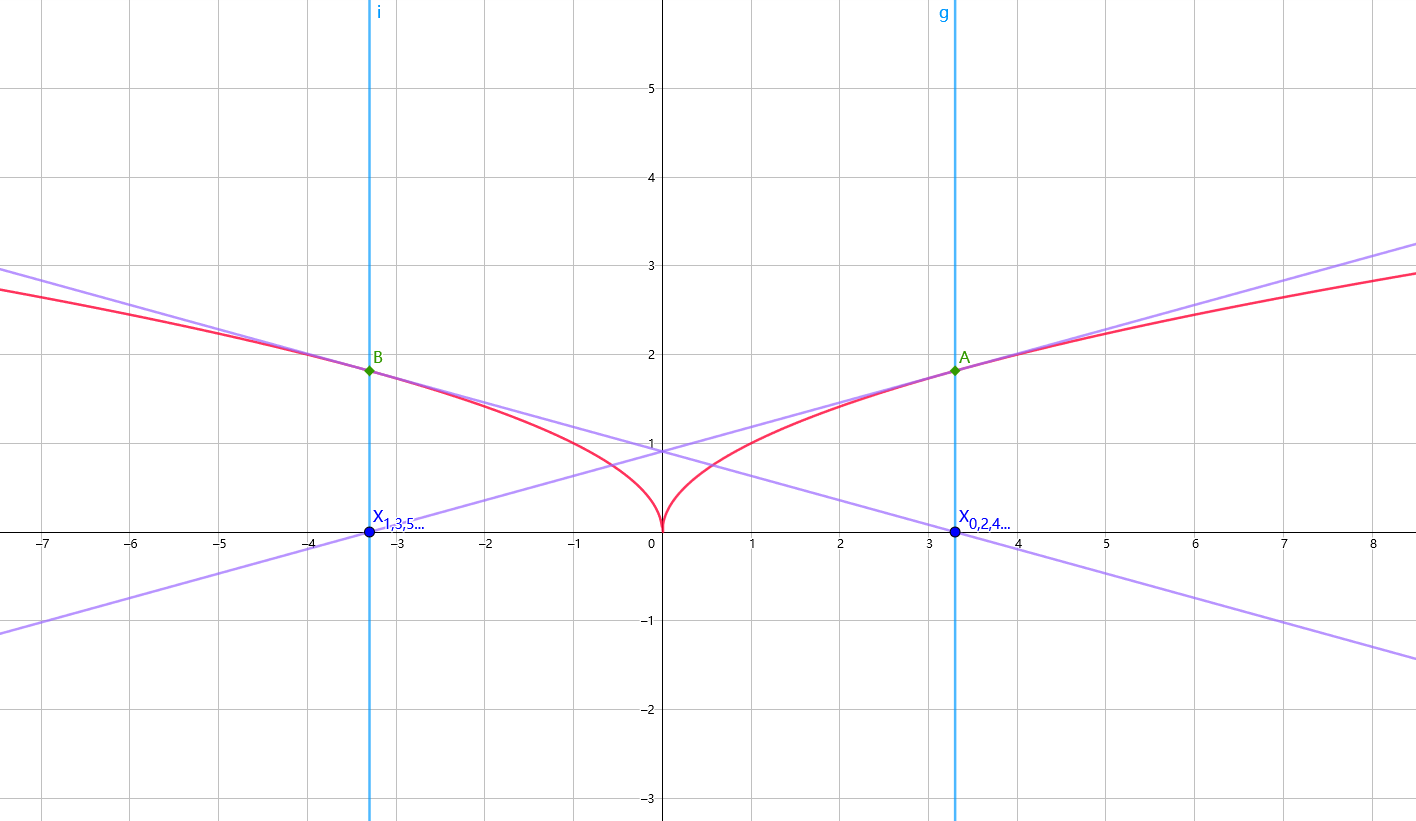
算法对 \(x_0\) 和精度 \(\omega\) 的选取有较高要求。在牛顿迭代法中，\(f(x)\) 的根对应每个 \(x_0\) 构成牛顿分形，其满足一条性质：若 \(\exist x_0 \in [a,b]\) 能使得其通过无限次迭代后归于某一根，那么对于 \(\forall x_0 \in [a,b]\) ，迭代要么所有 \(x_0\) 都归于同一个根，要么能归于所有根。
