[安乐椅#3] 拉尔瓦定理

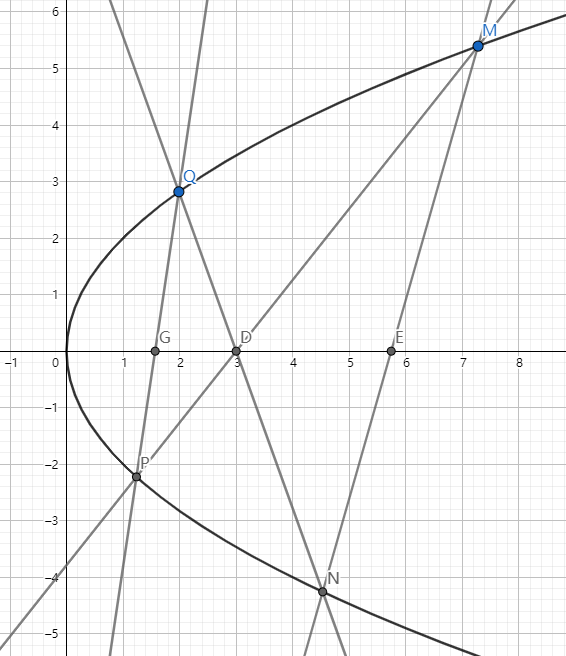
已知：抛物线 \(C:y^2=2px(p>0)\)，\(D(n,0),E(m,0)\) 为其对称轴上两点，\(M\) 是 \(C\) 上异于原点 \(O\) 的一动点，直线 \(ME\) 交 \(C\) 于 \(N\)，直线 \(MD\) 交 \(C\) 于 \(P\)，直线 \(MD\) 交 \(C\) 于 \(Q\)，直线 \(PQ\) 交 \(C\) 的对称轴于 \(G\)。

则：\(G\) 为定点 \((\dfrac{n^2}{m},0)\)。若 \(k_{QP},k_{MN}\) 均存在，则有 \(\dfrac{k_{QP}}{k_{MN}}=\dfrac{ED}{DG}\)。

更进一步：① \(E\) 为定点，② \(G\) 为定点，③ \(\dfrac{k_{QP}}{k_{MN}}\) 为定值，知一推三。

在椭圆和双曲线中也有类似的结论，两条直线斜率比仍为其二者与长轴交点距 \(D\) 距离比的倒数，\(G\) 仍为定点，但坐标表示就没有那么美观了：