薯片可吃性理论研究报告

by Fred & Gokix & Skull

一. 背景：相切可吃理论

一位清华学生在演讲中指出，薯片掉落到地面后与地面相切，接触面无限小，因而没有沾染细菌，拾起后可放心食用：

这一听上去荒谬的理论在提出之后引发热议，受到大量批驳与质疑，这一状况引发了我们的关注。

市面上常见的薯片分为弧形、鞍形和波浪形三种。我们计划利用数学工具对两种薯片的形状进行拟合，建出模型，观察其不同方向的截面形状，从而验证薯片可吃理论的合理性。

我们使用测绘工具对市面上4种不同品牌的薯片进行测绘，并使用Geogebra工具构建其对应模型。

二. 探究过程

1. 弧形薯片拟合

• 拟合方法

  法一：弧面本质上是柱面的一部分，是柱面被椭圆面截的产物。我们可以构建椭球与圆柱相交，进而得到弧面

  

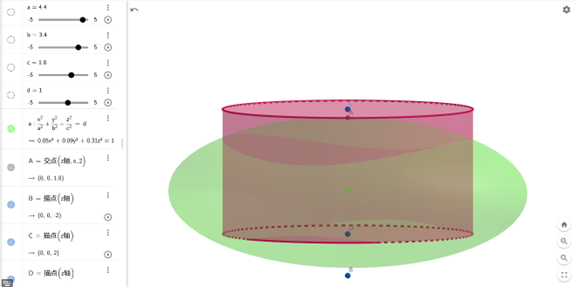
  法二：我们可以求出弧面的对应方程，在Geogebra中直接构建出弧面

  具体的，我们设 \(x=u\)，并尝试用 \(u\) 去表示 \(y\) 和 \(z\)。

  我们知道，柱面的表达式是 \(x^2+y^2=m\)，而椭圆面的表达式是 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\)，直接将二者联立并代入 \(x=u\)，可解得 \(\begin{cases} y=\sqrt{m-u^2} \\ z=\sqrt{1-\frac{u^2}{a^2}-\frac{m-u^2}{b^2}} \end{cases}\).将二式代入Geogebra的曲线函数即可获得弧面的边缘部分。

  

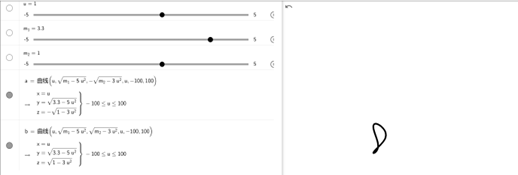
  法三：

  • 前置知识：二元函数

    对于平面图形，我们可以使用一元函数表示。同样，对于空间图形，我们可以引入二元函数

    设 \(D\) 是二元空间 \(\mathbf{R^2}\) 一非空子集，称映射 \(f:D \to \mathbf{R}\) 为定义在 \(D\) 上的二元函数，通常记为 \(z=f(x,y),(x,y)\in D\)

    其中点集 \(D\) 称为该二元函数的定义域，\(x,y\) 称为自变量，\(z\) 称为因变量，函数值 \(f(x,y)\) 的全体所构成的集合称为函数 \(f\) 的值域，记作 \(f(D)\)，即 \(f(D)=\{ z \mid z = f(x,y),(x,y) \in D \}\)

  我们考虑将半椭圆面表示成二元函数的形式，然后将柱面的表达式作为其定义域。

  即，通过移项，可得出半椭圆面的二元函数表达式为：\(z=\sqrt{c^2(1-\frac{x^2}{a^2}-\frac{y^2}{b^2})}\)，然后设定其定义域为 \(x^2+y^2 \le m\)，从而获得弧形薯片。

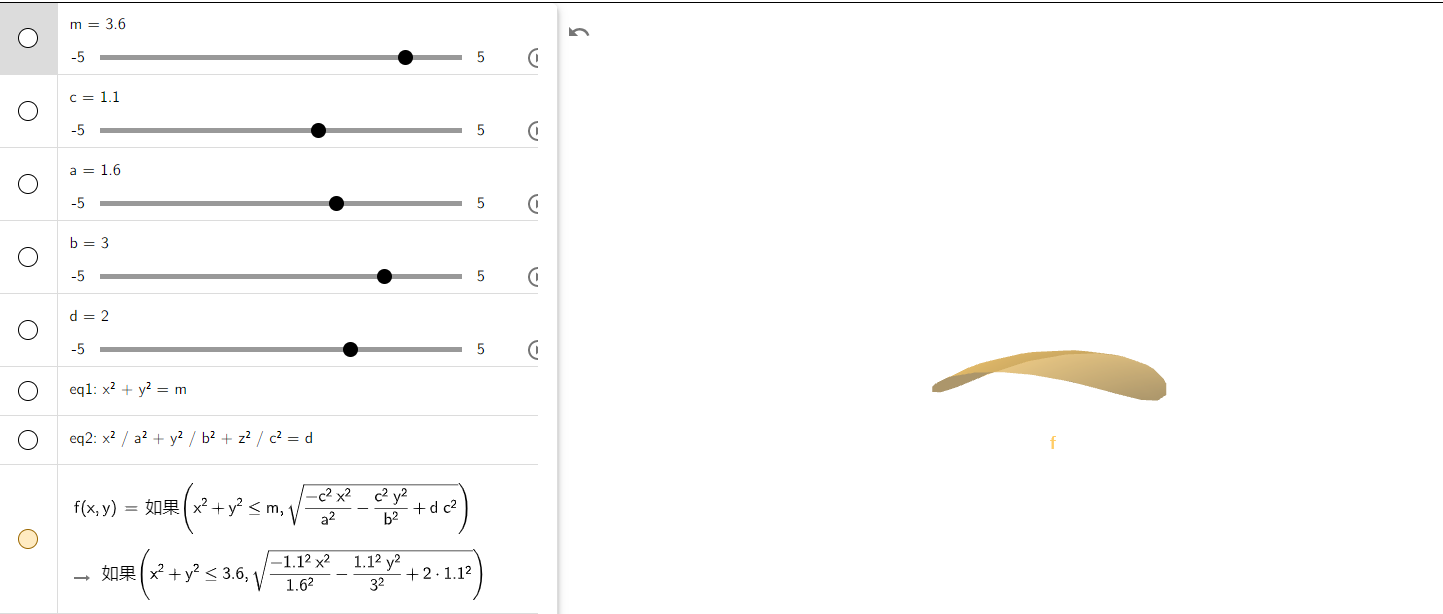
• 投影情况：

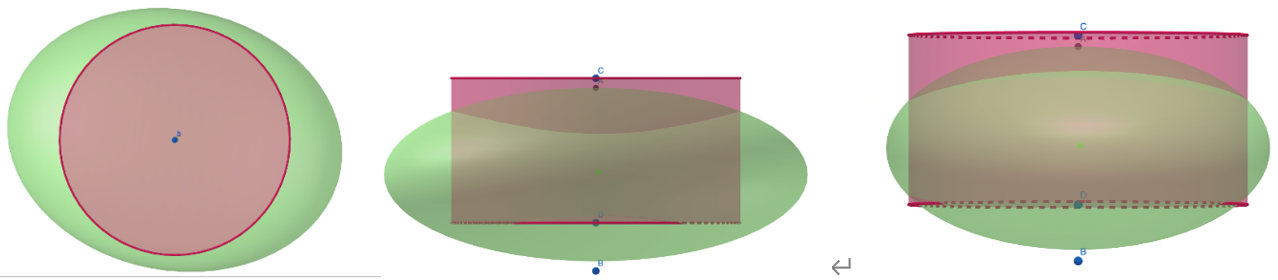
  经观察，弧面在上下方向上投影为椭圆（圆）；在侧面方向上投影为抛物线。

  当弧形薯片落地时，其与地面接触于弧形边缘两点（凹面）或弧形中间一条线段（凸面）

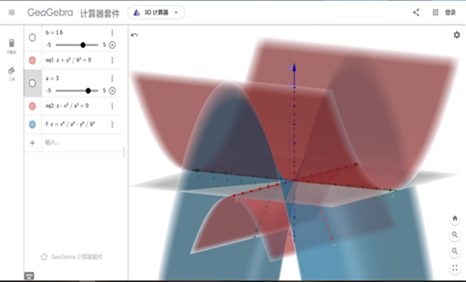
2. 鞍形薯片拟合

• 前置知识：双曲抛物面

  满足表达式 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=z,(a,b \text{为非零常数})\) 的所有点构成的集合为双曲抛物面。

  使用平面 \(x=x_0\) 或平面 \(y=y_0\) 截二元双曲面所获得的截面图形均为抛物线，使用平面 \(z=z_0\) 截二元双曲面所获得的的截面图形为双曲线。

  略证：用平面 \(x=0\) 截双曲抛物面即向其表达式中代入 \(x=0\)，得：\(z=-\frac{y^2}{b^2}\). 这很明显是一个只有二次项系数的抛物线。

  其余两面同理。

  

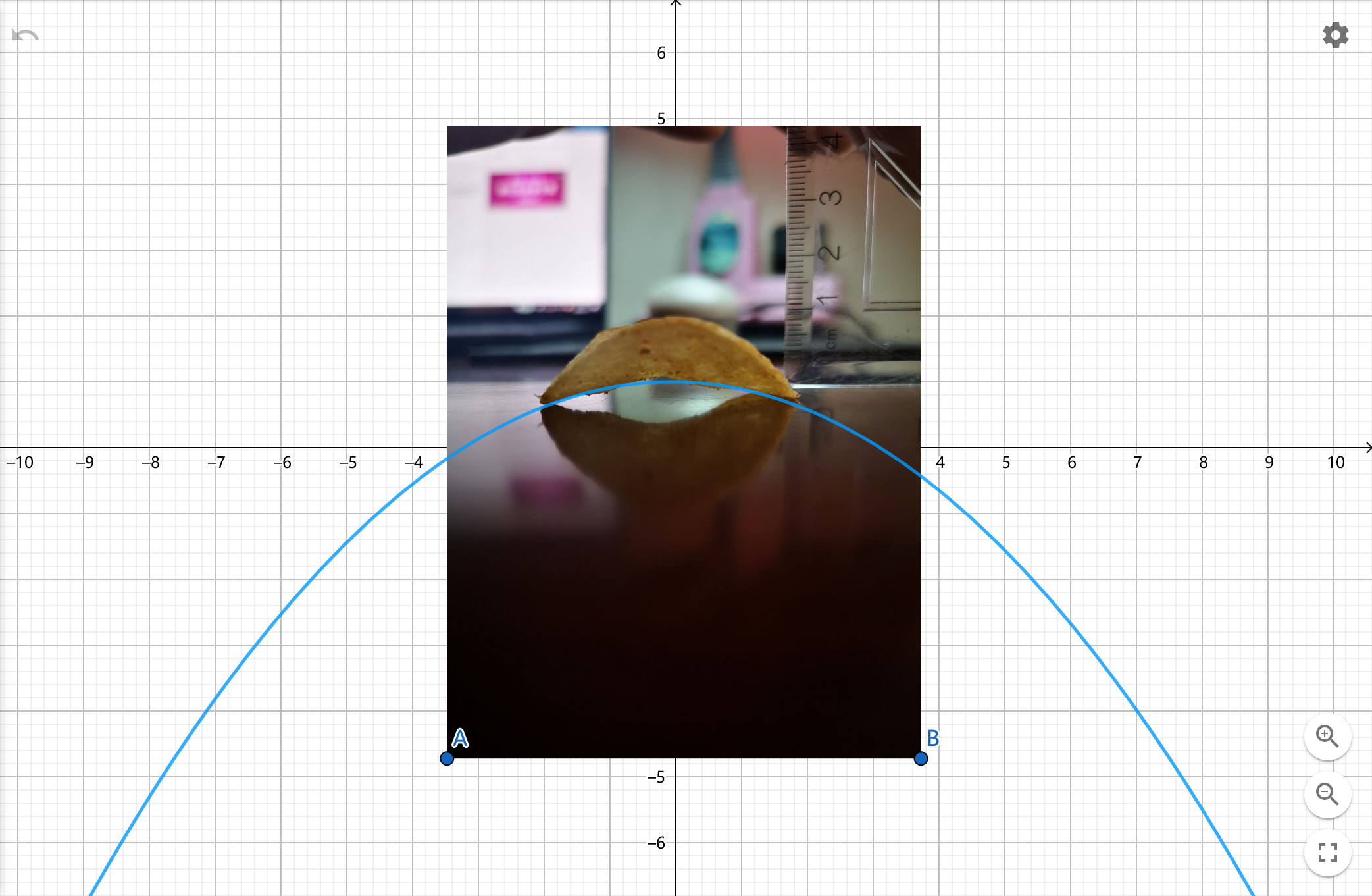
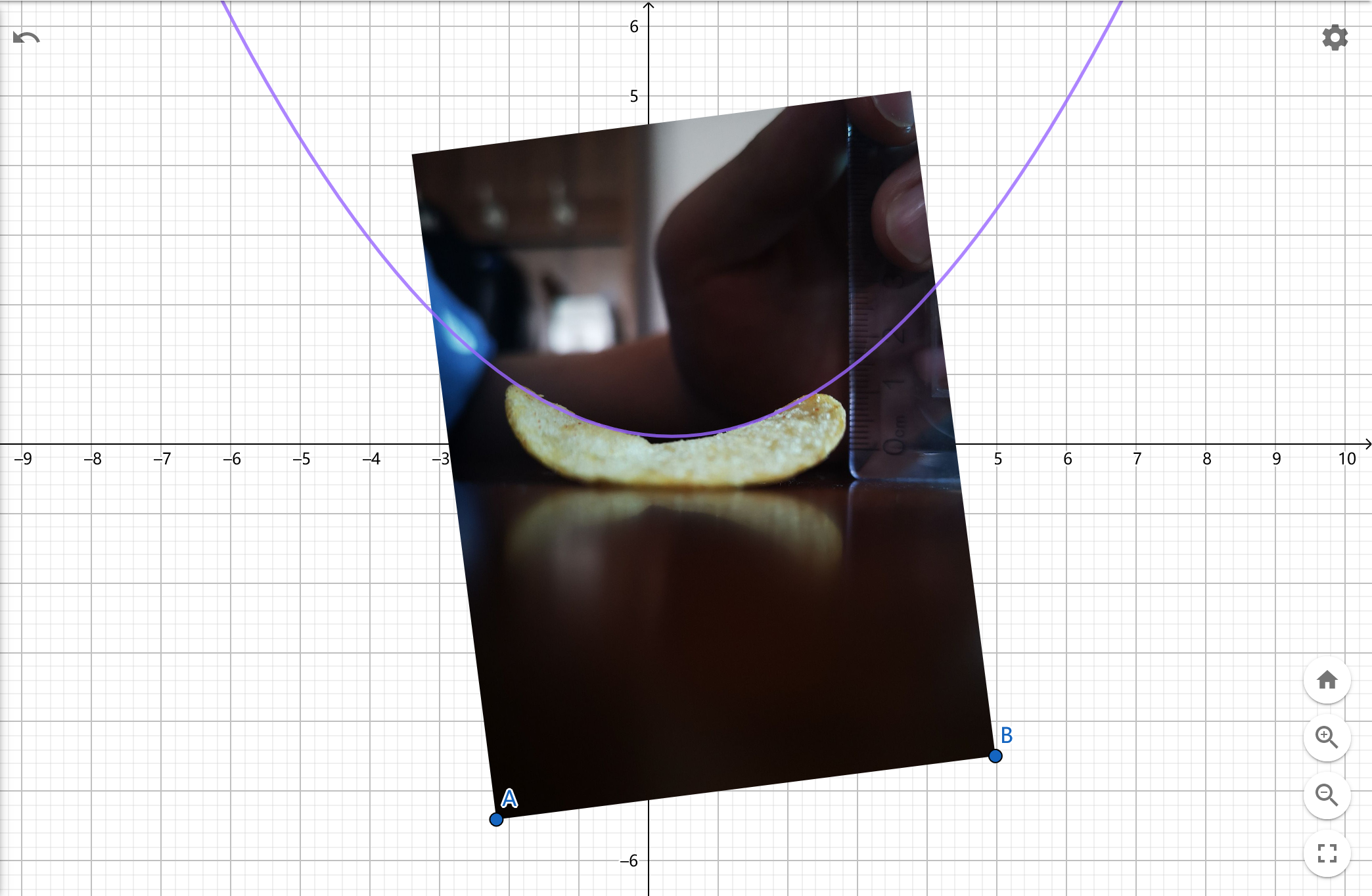
• 实际采样

  我们对实际的一块二元双曲面型薯片进行了测绘，并在Geogebra中拟合出了具体数值，之后还原出二元双曲面。

  1）俯视图

  拟合为椭圆，表达式为 \(\frac{(x+0.1)^2}{1.15^2}+\frac{(y+0.2)^2}{1.38^2}=2.4\)

  因为我们最终希望将二元双曲面的中心定在原点处，所以不需要 \(x_0,y_0\)，直接将原式化为 \(\frac{x^2}{1.15^2}+\frac{y^2}{1.38^2}=2.4\)

  

  2）主视图

  拟合内侧切抛物线，表达式为 \(y=-0.1x^2-0.01x+1\)

  直接删去一次项和常数项，理由是不管如何平移都不会影响二次项。故将原式化为化为 \(y=-0.1x^2\)

  解得 \(b=3.16\)

  

  3）侧视图

  侧视图的内侧切抛物线一定在平面 \(y=0\) 上，考虑用平面 \(y=0\) 截双曲抛物面得：\(z=\frac{x^2}{a^2}\)

  拟合的结果表达式为 \(y=0.15x^2-0.1x+0.12\)

  同理，只留 \(y=0.15x^2\)

  解得 \(a=2.58\)

  

• 拟合方法

  法一：使用椭圆柱面去截二元双曲面。

  但是这种方法并不直观。而且因为双曲抛物面不同于椭圆面，前者是一个二元函数，所以我们有更为便捷的法二。此处不再展示法一的具体实现。

  法二：使用Geogebra的if语句直接将椭圆表达式作为二元函数的定义域，Geogebra做出的图形直接就是所要的薯片模型。

  

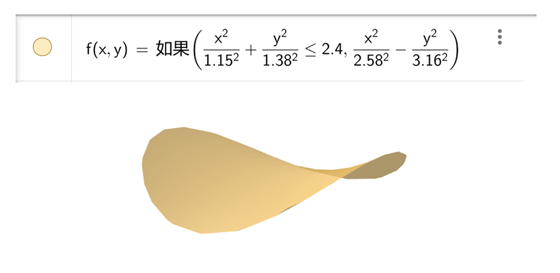
  法三：邓博文、孙豪阳、孙一鸣在其《生活启迪存真谛 几何代数薯片寻》提到了一种普适性更强的方法。但该方法依赖于多次取截面后积分，需要借助计算机进行计算。且该方法忽略薯片形状的表达式，故我们认为该方法更适用于薯片形状未知的情况，在此处不详细展开。

• 投影情况

  见实际采样中的三图，薯片在各方向投影情况如下：

  xOy:椭圆 yOz:抛物线 xOz:抛物线

  经测试，若一上下方向平面与薯片相切，则薯片“椭圆”边缘两点/“双曲线”中间两点与该平面相接。

3. 波浪形薯片拟合

• 拟合方法

  波浪形薯片的“波浪”使我们联想到周期函数，而根据实物图，我们发现“波浪”是一种周期曲线，因而我们使用正弦函数来拟合波浪形薯片。

  

  这里我们只考虑一种最简单的情况：假定“波浪”的上下表面各处于同一平面上。所以我们只用拟合 \(x\) 方向的正弦函数，即 \(f(x,y)=a \sin{(\omega x + \phi)}\)。

  类似于弧形薯片法三和鞍形薯片法二，我们使用椭圆柱定义域限制函数，从而得到波浪形薯片的拟合。

  

三. 结论

通过以上探究我们得知，在理想状态下，弧形薯片落地时会有两个点/一条线接地，而鞍形薯片则会有两个点接地。波浪形薯片可以看做多个弧形/鞍形薯片的聚合，因此也是以点/线接地。

在理想状态下，点和线的面积无穷小，因此可以看做薯片掉落接地后没有沾染细菌，“相切可吃理论具有一定合理性。

但是，我们由弹性力学可知，薯片在接触地面时会发生弹性形变。经弹性形变，原本接地的线就会变成矩形的面。因此，“相切可吃理论”虽然是一个有趣而大胆的论断，但它在实际生活中是不能实现的。

本理论局限性也非常大。一个很现实的问题是，真实薯片的形状是不规则的，它掉落后几乎不可能以理想的点/线接地 。

四. 引用资料

[1] 毕导THU：《相切可吃理论》

[2] 邓豪鸣：《生活启迪存真谛 几何代数薯片寻》