手电寸光探真谛 抛线焦点总堪寻
by Skull & S. & Fred & Gokix
一. 手电筒反射面与二元抛物面
前置知识:二元抛物面。
二元抛物面的解析式为:\(2pz=x^2+y^2\)。其相当于一条抛物线绕其对称轴旋转一周后形成的图形。相应的,其有一条性质:任意过二元抛物面对称轴的平面与二元抛物面的交线是抛物线。
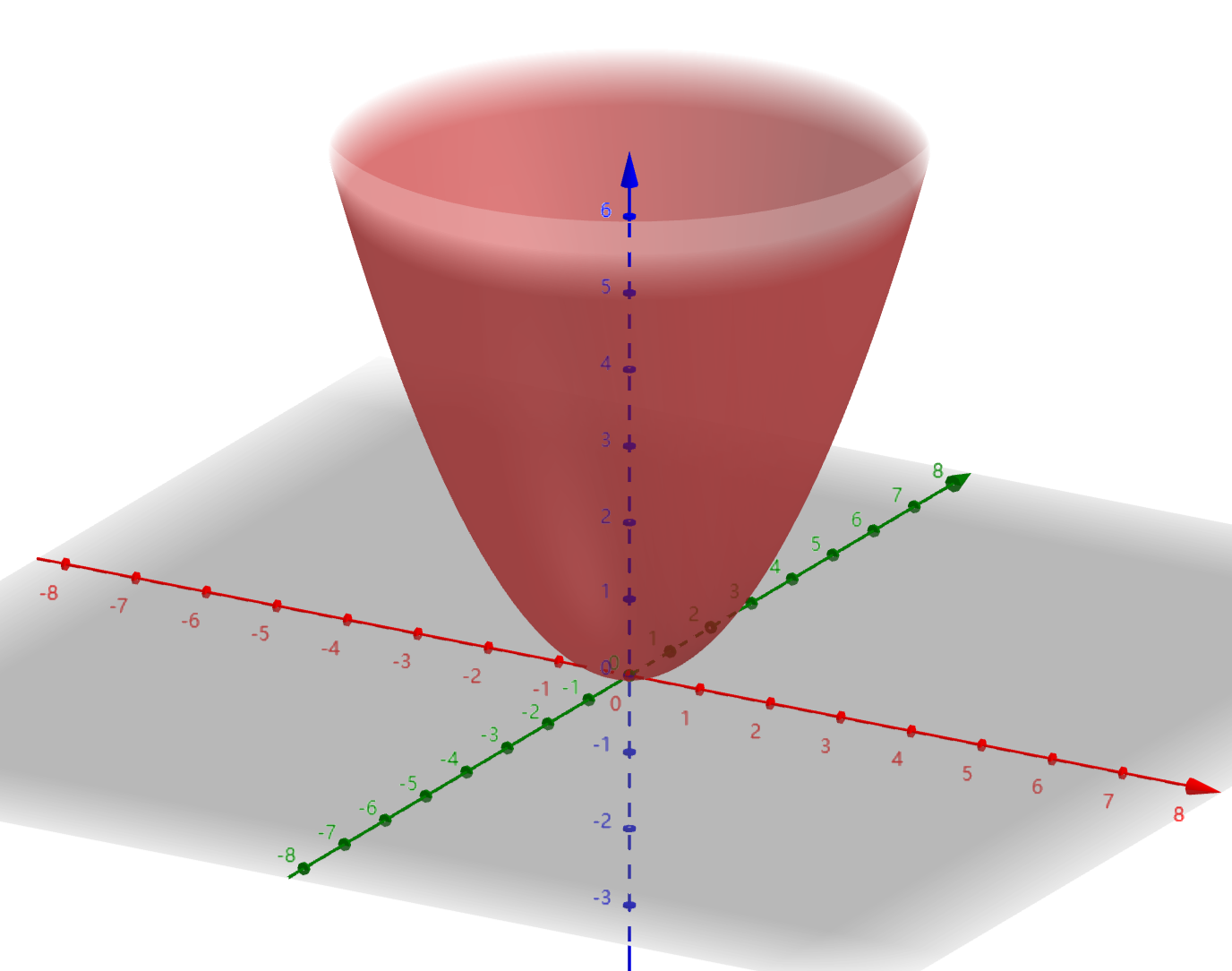

如图为一种手电筒的反射面,该种反射面的形状与二元抛物面类似。从而我们利用二元抛物面模型来研究手电筒中的光。
二. 抛物线的光学性质及其证明
直接研究二元抛物面不好研究,我们将二元抛物面平面化,利用其性质,将其转化为抛物线研究。
设抛物线 \(C:y^2=2px\)
其中, \(P(x_0,y_0)\) 为抛物线上任意一点 , \(l\) 为过 \(P\) 关于抛物线的切线 ,\(F(\dfrac{p}{2},0)\) 为抛物线的焦点。直线 \(PQ\) 为 \(l\) 的垂线
经查阅资料发现,在证明抛物线的光学性质过程中,常常将命题转化,转化为已知 \(PF‘\) 平行于 \(x\) 轴 ,去证明 \(\alpha=\beta\)
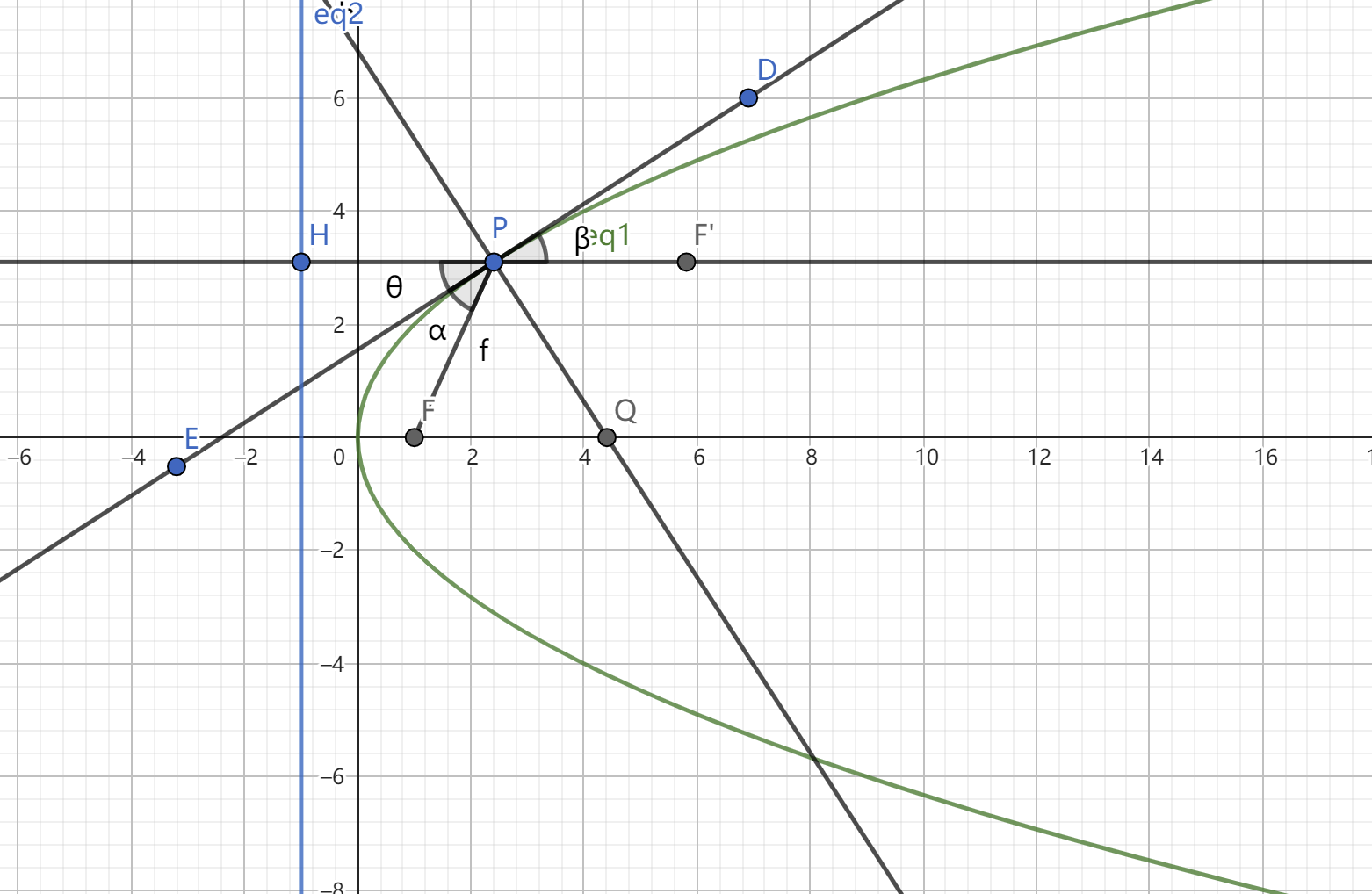
证法一:平行平分出等腰
我们发现如果 \(\alpha=\beta\) ,那么它们各自的余角相等,又由 \(PF'\) 平行于 \(x\) 轴可得 \(PF=PQ\) ,所以我们只要证明 \(PF=PQ\) ,就可以证明抛物线的光学性质。
根据抛物线的性质 \(PF=PH\) \(\therefore PF=x_0+\dfrac{p}{2}\)
先由 \(P\) 点的切线即为点 \(P\) 关于 \(C\) 的极线,再利用垂直,
表示 \(l_{PQ}:y-y_0=-\dfrac{y_0}{p}(x-x_0)\)
将 \(y=0\) 代入拿到 \(Q(x_0+p,0)\)
于是 \(|FQ|=|OQ|-|OF|=x_0+p-\dfrac{p}{2}=x_0+\dfrac{p}{2}\)
不难得到 \(|FQ|=|FP|\)
综上,抛物线光学性质得证。
证法二:到角公式
要证明角相等,在斜率均已知的情况下,可以直接使用到角公式
焦点 \(F\) 的坐标为 \((\dfrac{p}{2},0)\) \(\therefore\) 直线 \(PF\) 的斜率 \(k_{PF}=\dfrac{y_0}{x_0-\dfrac{p}{2}}\)
进而垂线 \(PQ\) 的斜率 \(k_{PQ}=-\dfrac{y_0}{p}\)
由 \(PF'\) 平行于 \(x\) 轴可知 \(k_{PF'}=0\)
于是表示 \(\tan \angle QPF=\dfrac{k_{PQ}-k_{PF}}{1+k_{PQ}k_{PF}}=-\dfrac{-\dfrac{y_0}{p}-\dfrac{y_0}{x_0-\dfrac{p}{2}}}{1-\dfrac{y_0}{p}\cdot \dfrac{y_0}{x_0-\dfrac{p}{2}}}=-\dfrac{y_0(x_0+\dfrac{p}{2})}{p(x_0-\dfrac{p}{2})-y_0^2}\)
又\(\because y_0^2=2px_0\) ,代入上式得,\(\tan \angle QPF=\dfrac{y_0(x_0+\dfrac{p}{2})}{p(x_0+\dfrac{p}{2})}=\dfrac{y_0}{p}\)
再表示 \(\tan \angle QPF'=\dfrac{k_{PF'}-k_{PQ}}{1+k_{PF'}k_{PQ}}=\dfrac{y_0}{p}\)
于是得到 \(\tan \angle QPF=\tan \angle QPF'\) \(\therefore \angle QPF=\angle QPF'\)
综上,抛物线的光学性质得证。
证法三:证明中垂线
我们发现有对顶角 \(\theta=\beta\) ,所以证明 \(\alpha=\beta\) 可以转化为 \(\theta=\beta\) ,而如果 \(l\) 为 \(HF\) 的中垂线,则抛物线的光学性质得证。
有 \(F(\dfrac{p}{2},0),H(-\dfrac{p}{2},y_0)\)
可得 \(k_{FH}=-\dfrac{y_0}{p}\)
根据极点极线可得, \(l:y_0y=2p\cdot \dfrac{x_0+x}{2}=px+px_0\)
于是 \(k_l=\dfrac{p}{y_0}\) 且 \(k_l\cdot k_{FH}=-1\) 即 \(FH\) 垂直于 \(l\)
设 \(FH\) 的中点为 \(N(0,\dfrac{y_0}{2})\) ,将 \(x=0\) 代入 \(l\) 得,\(y=\dfrac{px_0}{y_0}\)
又\(\because y_0^2=2px_0 \therefore p=\dfrac{y_0^2}{2x_0}\)
将 \(p\) 回代可得到, \(y=\dfrac{\dfrac{y_0^2}{2x_0}\cdot x_0}{y_0}=\dfrac{y_0}{2}\)
于是可得 \(FH\) 的中点在 \(l\) 上,所以 \(l\) 为 \(FH\) 的中垂线
综上,抛物线的光学性质得证。
证法四:反证法

总结来说抛物线中光学性质的证明相比来说,比椭圆的光学性质证明起来相对容易,证法一和证法三利用极点极线相关知识可以大量简便计算,并且都应用了一定的几何知识,使解析几何的计算量减少,而证法二到角公式就是纯粹的解析几何的证明方式。
部分一中给出的那个手电筒的光源约位于反射面的焦点位置,而手电筒打出的光主要部分的面积和手电筒口的面积差不多相等,表明该手电筒射出的光基本是平行光。也印证了我们的推理。

三. 边缘增强效应
然而,可以明显地注意到:上图中手电筒射出的光的主要部分的四周有明显的一个亮圈。通过与手电筒内部结构比较,为了安装光源而去除的部分反射面的大小远小于中间较暗部分的大小。这其中是否藏有玄机?
经过探索,我们给出了一种解释:
边缘增强效应:对于一个使用理想光源(均匀向四周发射光线的光源)、以二元抛物面为反射面的手电筒,在忽略其余光学原件对光路产生的影响的情况下,当光源低于焦点或在焦点附近时,会在出射光边缘形成一个亮光圈。
出现这个效应的原理是:在抛物面内多次反射次数越多的光越趋向于在抛物面边缘射出。
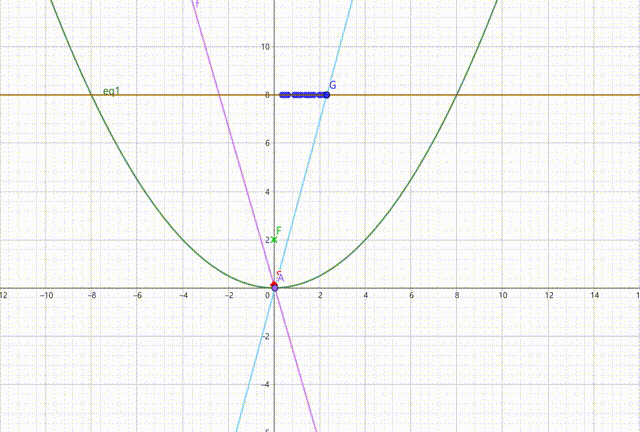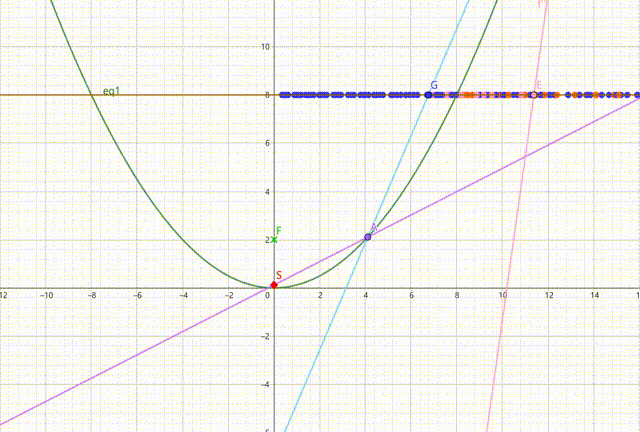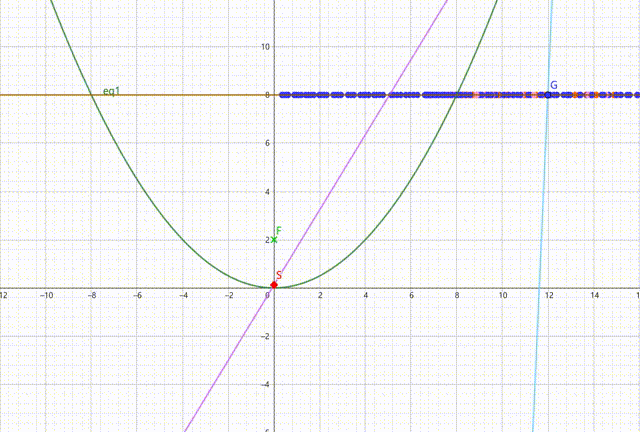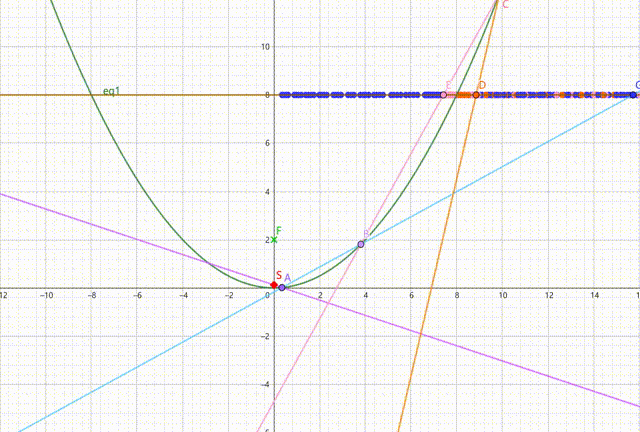
下图中,黄线以下部分为手电筒反射面,而紫、蓝、粉、橙色直线(应该用射线,但用直线表示便于作画)依次表示入射光、第一反射光、第二反射光、第三反射光。随入射光出射角变化,作出三条反射光线与黄线的交点的轨迹(仅作出对称轴右侧部分,左侧是对称的)。可以发现,在抛物线内部的部分,第一反射光交点轨迹全部占满黄线,第二反射光交点仅占黄线右侧一小部分,第三反射光交点占黄线右侧更小的一部分。
由此可见,介于入射光未经反射即出射的光基本是均匀的,一个点的光照强度在理想条件下主要取决于过这个点的光的条数。而靠近边缘的部分经过的光的条数要多于中间部分,故会形成一个亮圈。
下面浅要解释一下这个现象的原因。
设抛物线为 \(2py=x^2(p>0)\)
为了便于解释,以下命题的成立均需要一个共同的前提条件:第一反射点(A点)的纵坐标大于出射点(S点)的纵坐标。虽然A点低于S点在一般手电筒内均成立,但讨论麻烦,故不做说明。
同时,仅考虑对称轴右侧光线。左侧光线是完全对称的。
结论1:对于一个反射点,其反射光线斜率大于入射光线斜率。
证明:设抛物线为\(2py=x^2\),反射点为\(N(a,\frac{a^2}{2p})\),入射光线斜率为 \(k_1\),反射光斜率为 \(k_2\).
通过求导,不难得出\(N\)点处的切线斜率 \(k_0=\frac{a}{p}\)。
由于抛物线右侧是下凸增的,所以 \(k_0>k_1\).
根据到角公式,有 \(\frac{k_2-k_0}{1+k_2k_0}=\frac{k_0-k_1}{1+k_1k_0}\)
解得 \(k_2=\frac{k_1k_0^2-k_1+2k_0}{1+k_0^2}\).
下面比较 \(k_1\) 与 \(k_2\) 的大小,利用作差法,得:
\(\frac{k_1k_0^2-k_1+2k_0}{1+k_0^2}-k_1=\frac{2(k_0-k_1)}{1+k_0^2}\)
\(\because k_0>k_1\)
\(\therefore 上式>0\)
\(即,k_2>k_1\).
\(\Box\)
因为第一条入射光的斜率是正的,结论1证明了光线的斜率在一次反射中会变大,从而归纳地证明了光线的斜率一直是正的而且会越来越大。
这点非常重要,它说明了光即使在反射,也会“顺着”抛物线的图象走,而不会在抛物线的两端“乱跑”的行为。
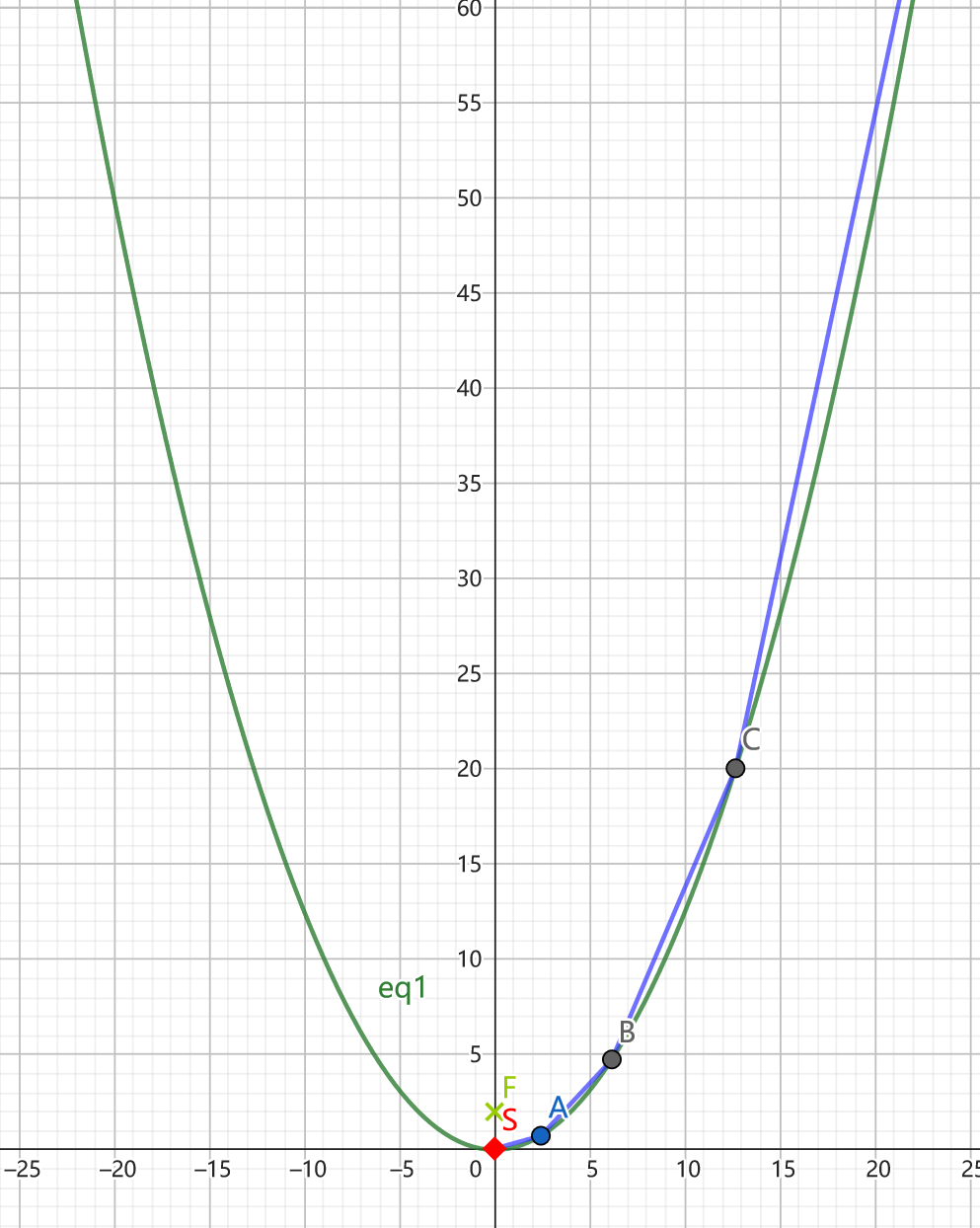
结论2:任何光在手电筒内的反射次数都是有限的。
结论1说明了光线会沿手电筒反射壁上升,直至射出手电筒。如果存在无限反射的情况,那只能是收敛。这点以我的能力暂时还无法严谨证明,但是根据抛物线的相似性,假如存在某束光线是收敛的,那必然对于任意抛物线都会存在这一束光线。但是,根据开头给出的例子,对于 \(8y=x^2\) 是不存在这束光线的,从而说明不存在这束光线。
结论2说明完毕。
根据结论2,任意光线最终都会射出手电筒。而根据结论1,光线反射越多次,其就越偏向于在手电筒边缘射出。如果简单地将光线条数作为亮度的主要衡量标准,就会出现该效应。
当然,我们知道,边缘增强效应有不小的局限性。其一,第一反射点高于出射点的假设本身对效应就有一定干扰。虽然说结论1的证明与该假设无关,但之后的归纳奠基就不成立了,从而导致一部分光在某些时刻斜率可能为负,难以确定其最后从手电筒的哪里射出。其二,现实生活中,简单地将光线条数作为亮度的主要衡量标准并不客观。随着反射次数的增多,反射面对光的吸收作用会逐渐加强。其三,光源的均匀发光是针对于角度来说,而不是针对于长度。不经任何反射、直接从光源发射出手电筒的光应当是中间亮而四周疏的。举个例子:一顶吊灯的正下方会比其正下方五米远的地方亮。