利用三视图还原双曲抛物面

俯视图

拟合为椭圆，作为最终双曲抛物面二元函数的定义域。没啥好说的。

e.g. \(\frac{(x+0.1)^2}{1.15^2}+\frac{(y+0.2)^2}{1.38^2}=2.4\)

因为我们最终希望将二元双曲面的中心定在原点处，所以不需要 \(x_0,y_0\)，直接将原式化为 \(\frac{x^2}{1.15^2}+\frac{y^2}{1.38^2}=2.4\)

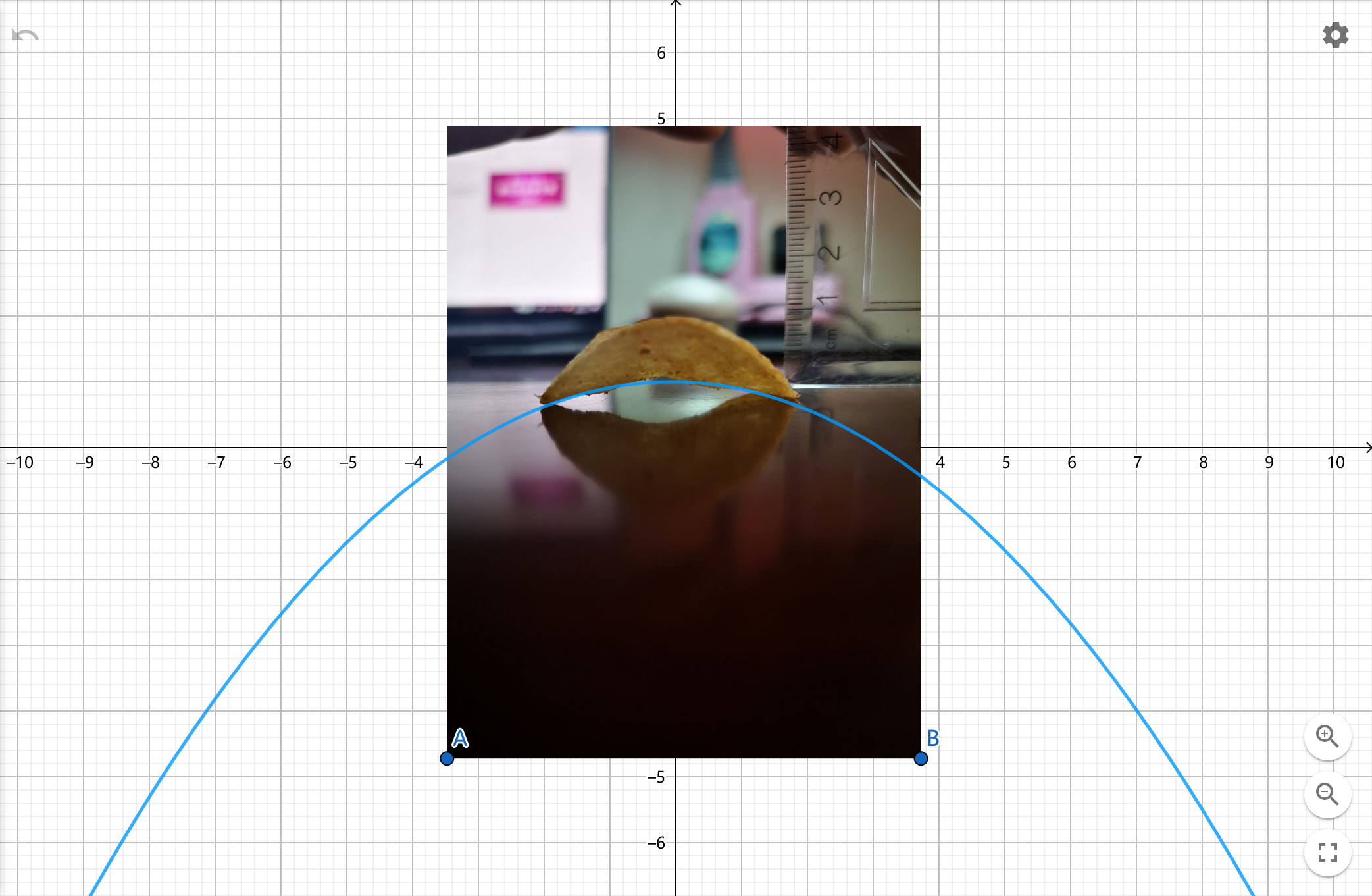
主视图

拟合内侧切抛物线。钦点用抛物线去拟合是为了满足二元双曲面的要求。

主视图的内侧切抛物线一定在平面 \(x=0\) 上，考虑用平面 \(x=0\) 截双曲抛物面得：\(z=-\frac{y^2}{b^2}\)

这很明显是一个只有二次项系数的抛物线。

e.g. \(y=-0.1x^2-0.01x+1\)

直接删去一次项和常数项，理由是不管咋平移都不会影响二次项。化为 \(y=-0.1x^2\)

解得 \(b=3.16\)

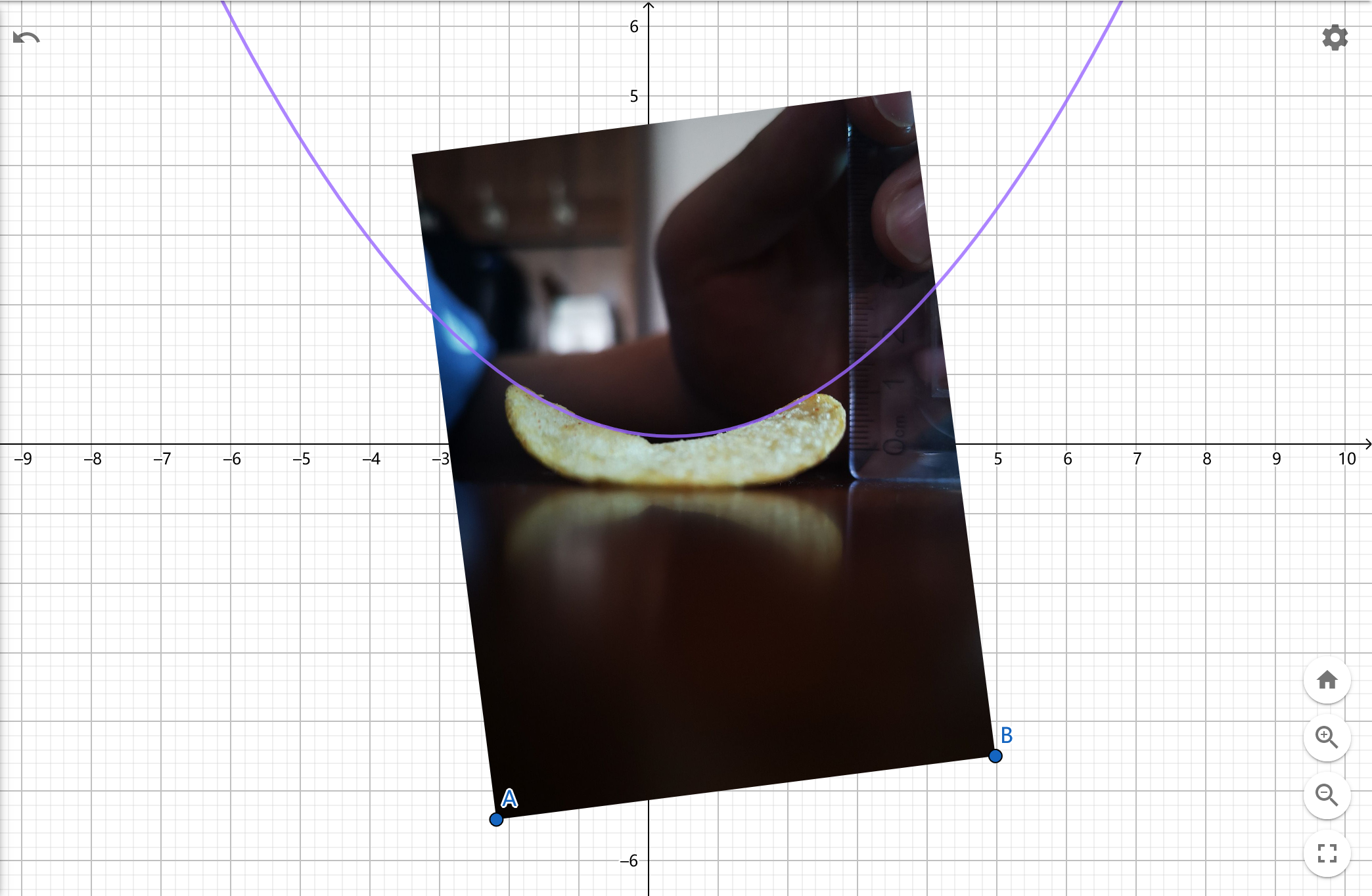
侧视图

同理。侧视图的内侧切抛物线一定在平面 \(y=0\) 上，考虑用平面 \(y=0\) 截双曲抛物面得：\(z=\frac{x^2}{a^2}\)

这很明显是一个只有二次项系数的抛物线。

e.g. \(y=0.15x^2-0.1x+0.12\)

同理，只留 \(y=0.15x^2\)

解得 \(a=2.58\)

还原

联立得：

\[\begin{cases} f(x,y)=\frac{x^2}{2.58^2}-\frac{y^2}{3.16^2}\\ \frac{x^2}{1.15^2}+\frac{y^2}{1.38^2}\le2.4\end{cases} \]

然后你就可以发现这个东西其实和原来的薯片区别挺大的

究其原因呢，还是因为现实中的薯片千奇百怪，而我们选择的这一片“很像”双曲抛物面的薯片其实和双曲抛物面还是有不小区别的。而且这些区别我们并不好消除，见下图：

同一薯片内切线的 3 种不同的拟合↑