障碍函数法

障碍函数法直接对线性规划标准形式的变式进行操作。

\(\max z= \sum\limits_{j=1}^{n} c_j x_j\)

\(s.t. \begin{cases} \sum\limits_{j=1}^n a_{ij}x_j \le b_j,i=1,2,\dots,m \\ x_j \ge 0,j=1,2,\dots,n\end{cases}\)

注意此处与标准形式的唯一区别是约束条件中的等号变为小于等于号。两者是等价的，因为根据定理2，线性规划问题的最优决策必然于边界处取得，而小于的部分则只是可行域的内部，这些部分不可能取得最优决策，但是却可以帮助我们转移决策点。

接下来对约束条件进行变形：

\(\Rightarrow \sum\limits_{j=1}^n a_{ij}x_j - b_j\le 0\)

同时记左式为 \(\Upsilon_i\)

考虑构造一个函数 \(I(\Upsilon_i)\)，使得其函数值在 \(\Upsilon_i \le 0\) 时与0接近，而当 \(\Upsilon_i>0\) 时为正无穷，则可以将线性规划问题转变为函数的近似形式：

\(\max z= \sum\limits_{j=1}^{n} c_j x_j + \sum\limits_{j=1}^{n} I(\Upsilon_i)\)

\(s.t. x_j \ge 0,j=1,2,\dots,n\)

精度最佳的 \(I(x)\) 自然是 \(I(x)=\begin{cases} 0,x \le 0 \\ +\infty,x>0\end{cases}\)，但是这样选取会导致估价函数无法求最值。一种经典的近似选取是 \(I(x)=\begin{cases} -\log_{a}(-bx),(a>1,b>0),x \le 0 \\ +\infty,x>0\end{cases}\).

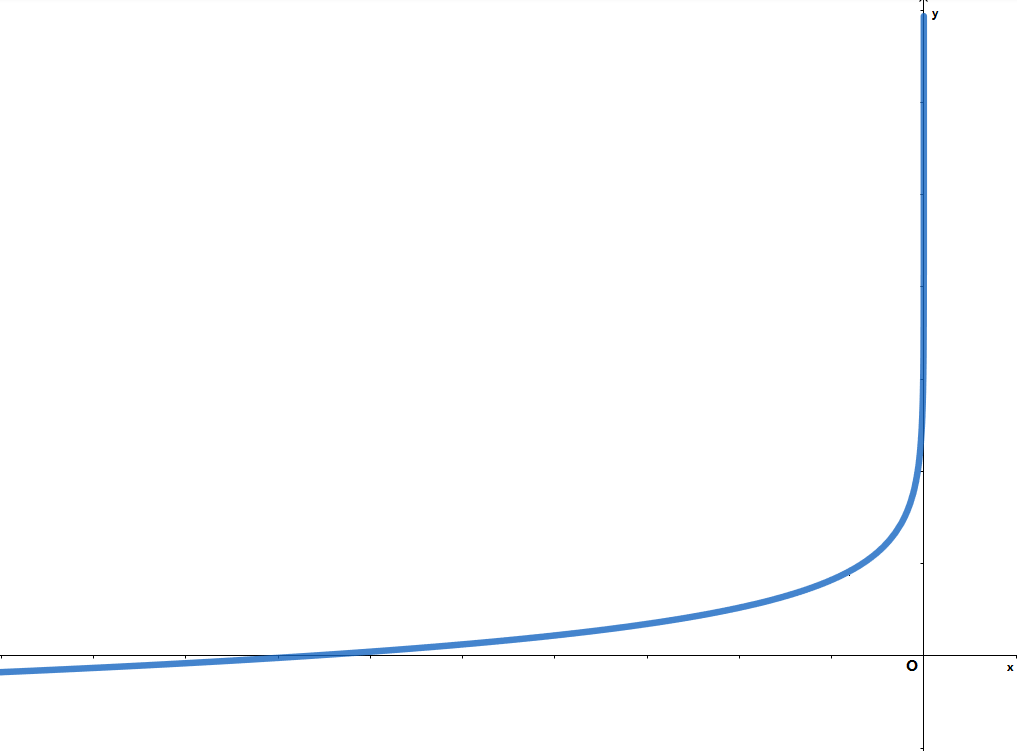
该函数在 \(x\) ”比较负“的情况下，\(I(x)\approx 0\)。而当 \(x\) 趋近于 \(0^-\) 时，函数值迅速增大至正无穷。这时 \(I(x)\) 就成为一个障碍函数，阻止 \(x\) 的进一步增大。

而且这样选取 \(I(x)\) 还有一个好处就是使估价函数的最值容易求得。由于估价函数 \(n\) 阶可导，所以直接对估价函数求偏导，然后使用牛顿迭代法求各项零点即可求得最值。

可以证明其时间复杂度为 \(\tilde{O}(n^{3.5})\)。