表达式

双曲函数

\(\operatorname{sh} x = \dfrac{e^{x}-e^{-x}}{2}\)

\(\operatorname{ch} x = \dfrac{e^{x}+e^{-x}}{2}\)

\(\operatorname{th} x = \dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\)

\(\operatorname{cth} x = \dfrac{e^{x}+e^{-x}}{e^{x}-e^{-x}}\)

\(\operatorname{sech} x = \dfrac{2}{e^{x}+e^{-x}}\)

\(\operatorname{csch} x = \dfrac{2}{e^{x}-e^{-x}}\)

反双曲函数

\(\operatorname{arsinh} x = \ln {(x+\sqrt{x^2+1})}\)

\(\operatorname{arcosh} x = \ln {(x+\sqrt{x^2-1})}\)

\(\operatorname{artanh} x = \dfrac{1}{2} \ln {\dfrac{1+x}{1-x}}\)

\(\operatorname{arcoth} x = \dfrac{1}{2} \ln {\dfrac{x+1}{x-1}}\)

\(\operatorname{arsech} x = \ln {(\dfrac{1}{x}+\sqrt{\dfrac{1}{x^2}-1})}\)

\(\operatorname{arcsch} x = \ln {(\dfrac{1}{x}+\sqrt{\dfrac{1}{x^2}+1})}\)

图像

• \(\operatorname{sh} x\) 与 \(\operatorname{ch} x\)

  

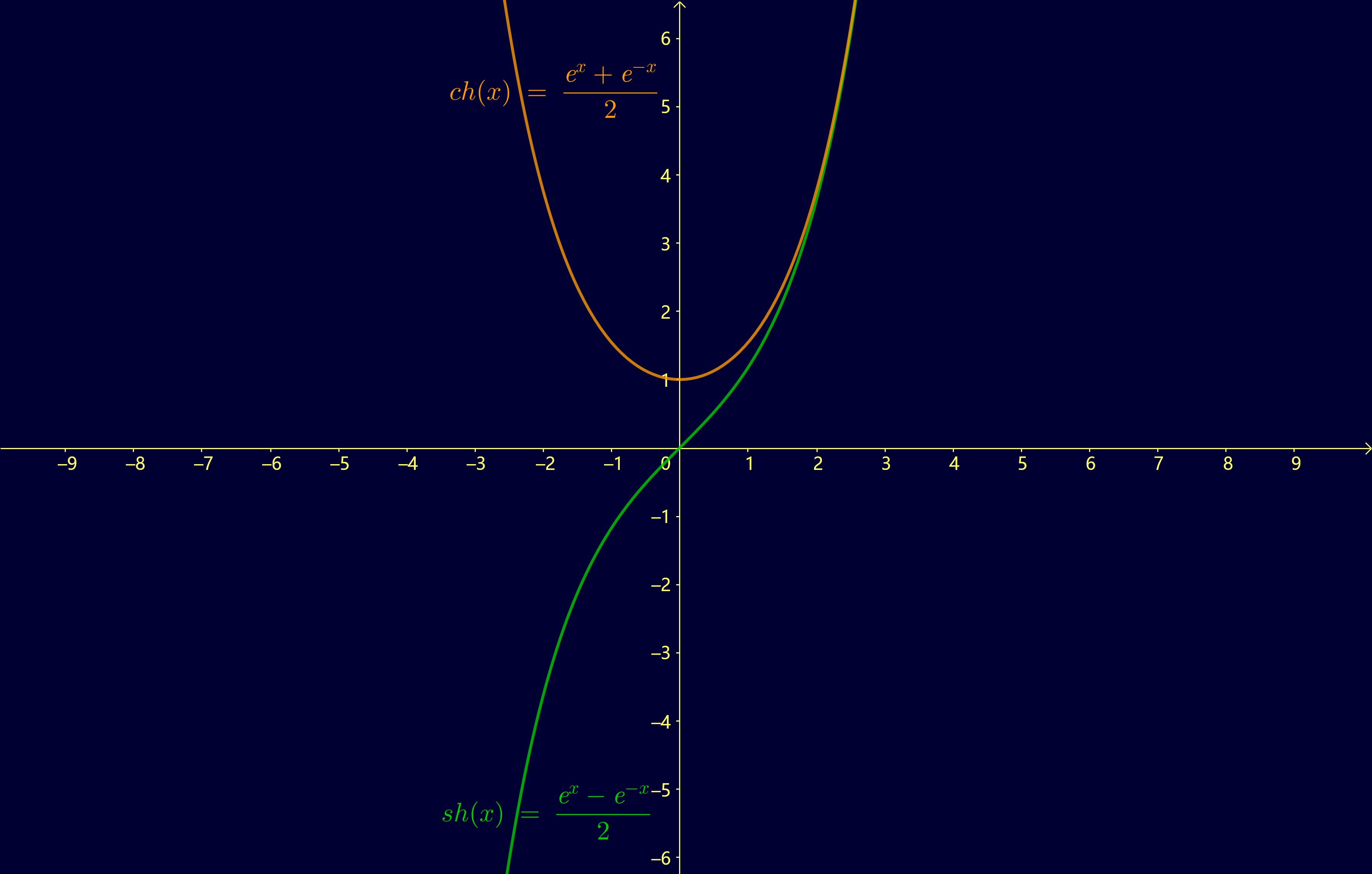
• \(\operatorname{th} x\) 与 \(\operatorname{cth} x\)

  

• \(\operatorname{sech} x\) 与 \(\operatorname{csch} x\)

  

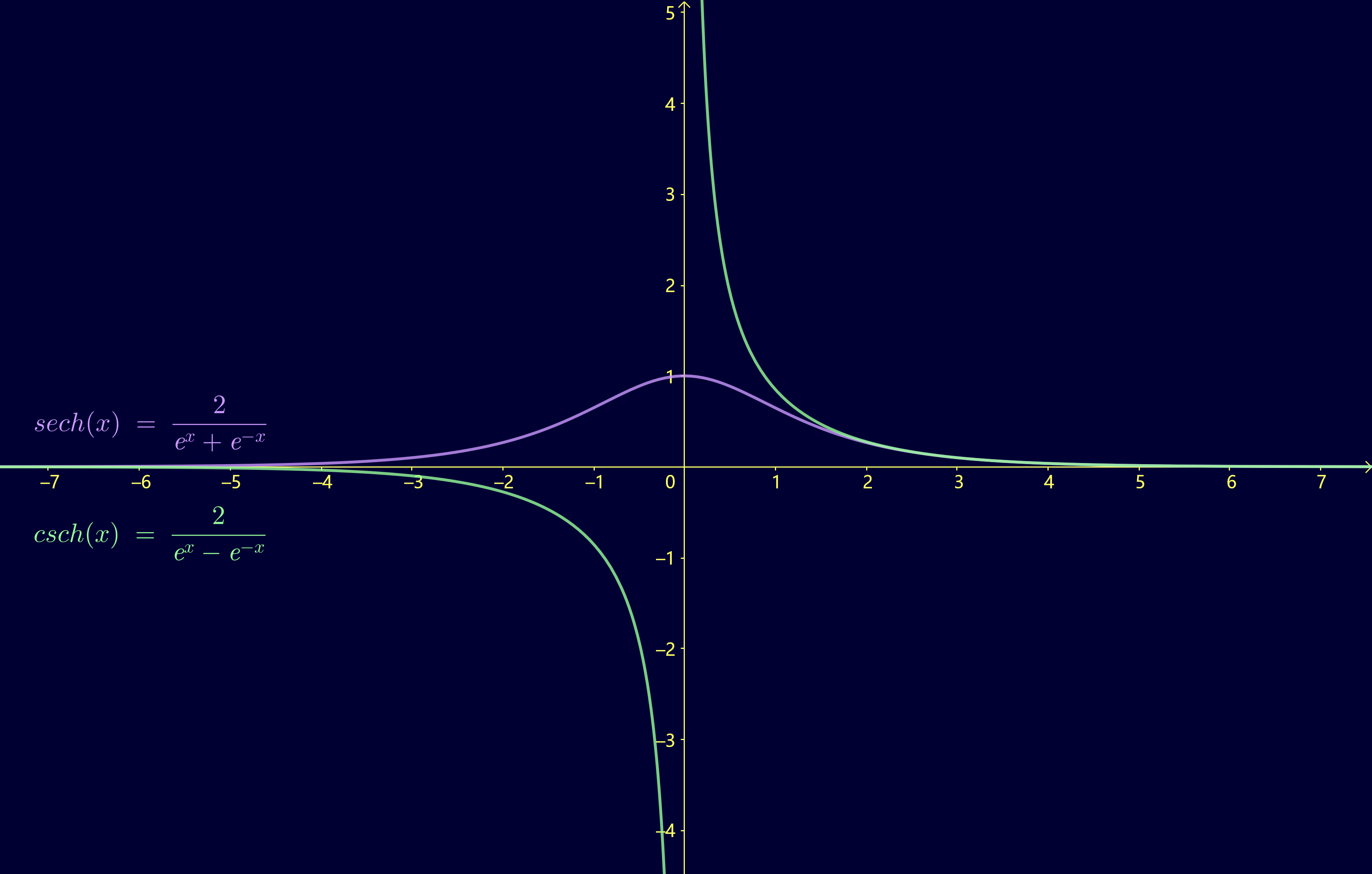
导数

\(\operatorname{sh}^\prime x = \operatorname{ch} x\)

\(\operatorname{ch}^\prime x = \operatorname{sh} x\)

\(\operatorname{th}^\prime x = \operatorname{sech}^2 x\)

\(\operatorname{cth}^\prime x = - \operatorname{csch}^2 x\)

\(\operatorname{sech}^\prime x = - \operatorname{sech} x \operatorname{th} x\)

\(\operatorname{csch}^\prime x = - \operatorname{csch} x \operatorname{cth} x\)

\(\operatorname{arsinh}^\prime x = \dfrac{1}{\sqrt{x^2+1}}\)

\(\operatorname{arcosh}^\prime x = \dfrac{1}{\sqrt{x^2-1}}\)

\(\operatorname{artanh}^\prime x = \dfrac{1}{1-x^2} \space (-1 < x < 1)\)

\(\operatorname{arcoth}^\prime x = \dfrac{1}{1-x^2} \space (x < -1 \space \or \space x > 1)\)

关系式

• \(\operatorname{ch}^2 x - \operatorname{sh}^2 x = 1\)

• \(\operatorname{sech}^2 x + \operatorname{th}^2 x = 1\)

• \(\operatorname{cth}^2 x - \operatorname{csch}^2 x = 1\)