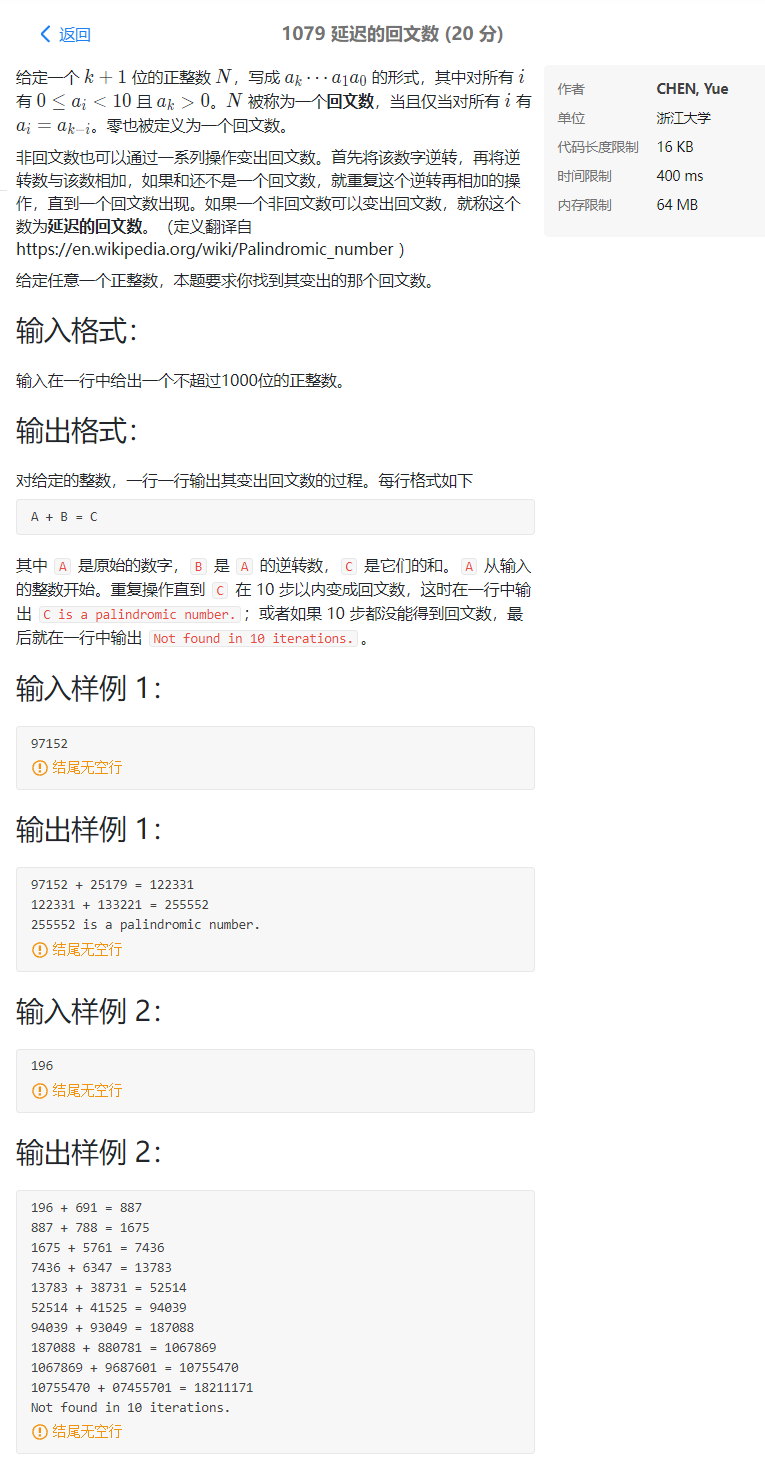
PTA 乙级 1079 延迟的回文数 (20 分) C++

 

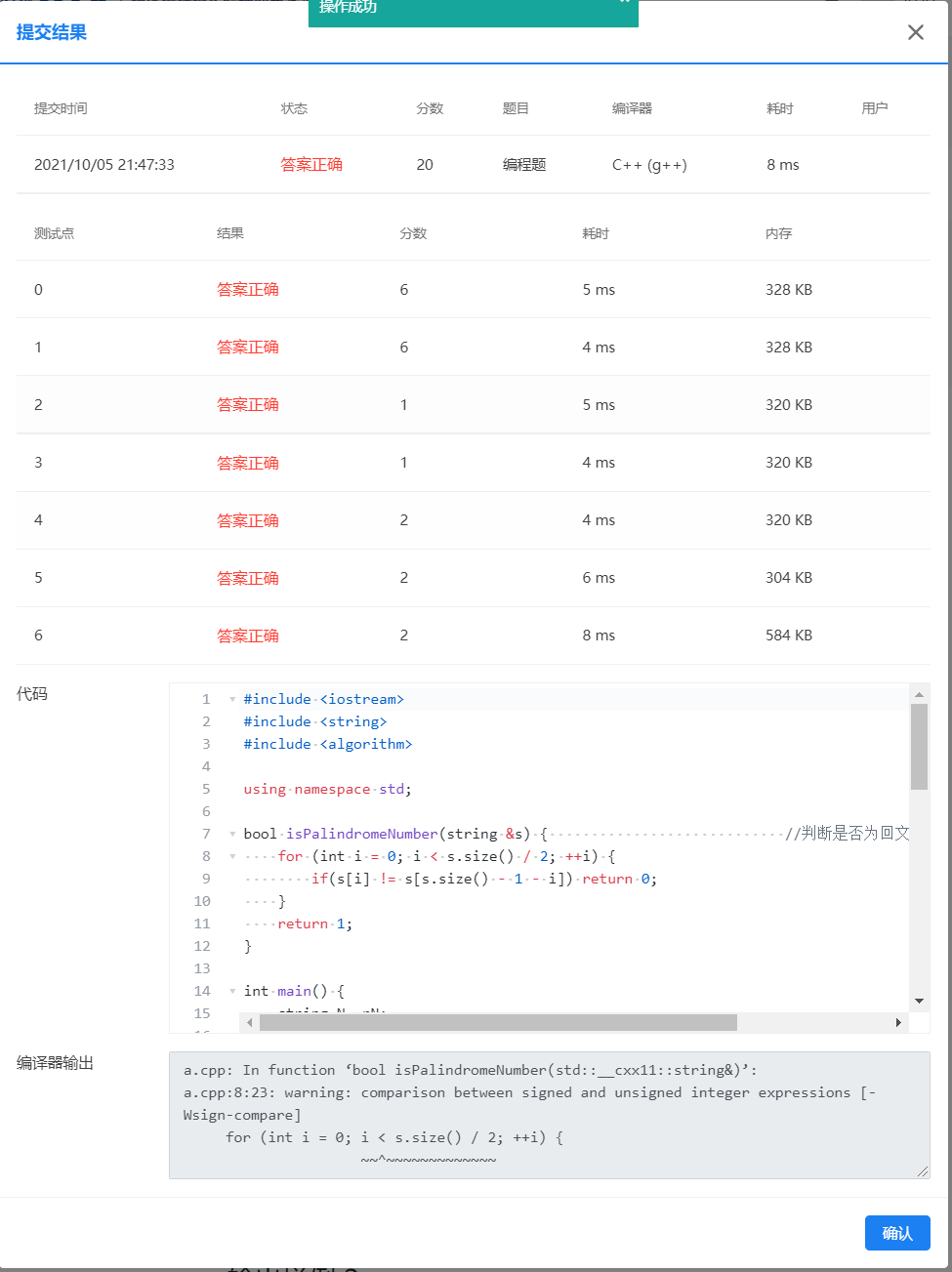
 测试点3,4,5是对输入N是否为回文数的判断

测试点6存在大数运算，不能单纯进行整数的加减，需要进行一位一位的处理

C++

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

bool isPalindromeNumber(string &s) {                            //判断回文数的函数
    for (int i = 0; i < s.size() / 2; ++i) {
        if(s[i] != s[s.size() - 1 - i]) return 0;
    }
    return 1;
}

int main() {
    string N, rN;
    string sum;
    cin >> N;
    bool N_judge = isPalindromeNumber(N);
    if (N_judge) {                                              //测试点3,4,5，首先对N进行判断是否为回文数
        cout << N << " is a palindromic number." << endl;
        return 0;
    }
    for(int i = 0; i < 10; ++i) {
        rN = N;
        reverse(N.begin(), N.end());
        int carry_bit = 0;
        for (int j = N.size() - 1; j >= 0; --j) {               //测试点6会进行大数运算，所以不能普通的整数加减，需要进行进位加法处理
            int tmp = (N[j] - '0') + (rN[j] - '0') + carry_bit;
            carry_bit = 0;
            if (tmp >= 10) {
                carry_bit = 1;
                tmp -= 10;
            }
            sum = to_string(tmp) + sum;
        }
        if(carry_bit) sum = to_string(carry_bit) + sum;         //判断加到最后是否存在进位
        bool judge = isPalindromeNumber(sum);
        cout << rN << " + " << N << " = " << sum << endl;
        if(judge) {
            cout << sum << " is a palindromic number." << endl;
            return 0;
        }
        N = sum;
        sum.clear();                                            //记得对加和的字符串进行清除，方便下一轮判断重复利用
    }
    cout << "Not found in 10 iterations." << endl;
    return 0;
}