机器学习算法 --- Naive Bayes classifier

一、引言

 　　在开始算法介绍之前，让我们先来思考一个问题，假设今天你准备出去登山，但起床后发现今天早晨的天气是多云，那么你今天是否应该选择出去呢？ 你有最近这一个月的天气情况数据如下，请做出判断。

• 这个月下雨的天数占10%
• 这个月早晨是多云的天数占40%        
• 在下雨的天数中早晨是多云的占50%        

 　　如果有普通本科的概率论知识，这个问题就不难解决，计算一下今天会下雨的概率，然后根据概率决定即可。解决方式如下：

　　　　

　　可以发现，今天下雨的概率只有12.5%，还是可以出去玩的（当然如果怕万一，那还是呆在家里）。

二、Bayes’s theorem

　　没错，上面的计算公式就是贝叶斯定理，这个定理的数学表示如下：

 

　　这个定理在日常生活中的应用非常广泛，比如：

• If dangerous fires are rare (1%) but smoke is fairly common (10%) due to barbecues, and 90% of dangerous fires make smoke. 如果烟雾报警器检测到有烟，请问发生火灾的可能为多少？

• Suppose that a test for using a particular drug is 99% sensitive and 99% specific. That is, the test will produce 99% true positive results for drug users and 99% true negative results for non-drug users. Suppose that 0.5% of people are users of the drug. What is the probability that a randomly selected individual with a positive test is a drug user?
• ....

　　对上述公式做一个变形如下：

　　在对其进行扩展则如下：

 

三、Naive Bayes Classifier

　　上面说了这么多，好像与机器学习分类器没啥关系啊！但是不是，是有关系的， Naive Bayes Classifier就是一种基于概率的分类器。

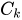　　首先，我们假设一组向量 ，这组向量的各个值表示某个数据的特征值，那么它属于某个类别  的概率就可用这个形式表示： 。

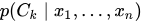　　根据上面的 Bayes’s theorem，这个概率的计算方法就如下：

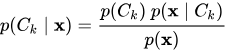　　（1）

　　对于条件概率的定义如下：

　　

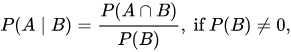
　　则,

　　=

　　可将上式写成如下形式：

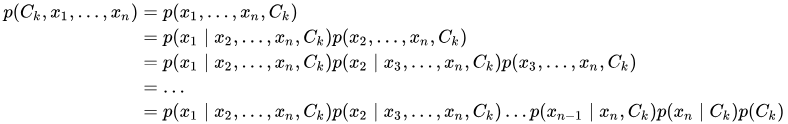　　（2）

　　然后，我们假设xi与xj(j不等于i)独立（即特征之间没有关系），则：

　　

　　则，对于（2）式(即（1）式右半部分的分母)，就可以写成如下形式：

　　

　　

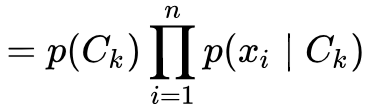
　　假设，则（1）式可以写成如下形式：

　　（3）

 　　通过（3）式，我们就可以计算一个数据属于某个类别的概率，分类结果也就是概率最大的那一个类别，所以Naive Bayes Classifier的完整表达形式如下：

　　

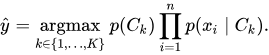
　　注意：由于在最后的结果比较中，每一个结果的计算都含有，即它不影响比较结果，可以直接忽略。 

四、说明

 　　关于Naive Bayes Classifier，我们假设了特征之间不存在任何关系，然而现实是特征之间是不可能没有关系的。比如对于水果的类别，它们的颜色，大小，重量之间比如存在某种联系；再比如对于人类的性别，身高与体重等特征也是存在联系的。但是，Naive Bayes Classifier往往会取得比较好的结果，如果对数据和样本能做一些合适的预处理，它取得的结果是非常好的。

 　　Naive Bayes Classifier在现实生活中的应用：垃圾邮件的分类，拼写检查与自动纠正，银行关于信用卡欺诈的检测等等。

 

五、参考与扩展链接

　　关于本篇文章的参考链接：https://www.mathsisfun.com/data/bayes-theorem.html

　　　　　　　　　　　　　　https://www.wikiwand.com/en/Bayes%27_theorem#　

　　　　　　　　　　　　　　https://www.wikiwand.com/en/Naive_Bayes_classifier 

　　这些链接中的很多知识本篇文章中还没有讲到，推荐大家去阅读学习。