机器学习算法 --- Decision Trees Algorithms
一、Decision Trees Agorithms的简介
决策树算法(Decision Trees Agorithms),是如今最流行的机器学习算法之一,它即能做分类又做回归(不像之前介绍的其他学习算法),在本文中,将介绍如何用它来对数据做分类。
本文参照了Madhu Sanjeevi ( Mady )的Decision Trees Algorithms,有能力的读者可去阅读原文。
说明:本文有几处直接引用了原文,并不是不想做翻译,而是感觉翻译过来总感觉不够清晰,而原文却讲的很明白清晰。(个人观点:任何语言的翻译都会损失一定量的信息,所以尽量支持原版)
二、Why Decision trees?
在已经有了很多种学习算法的情况下,为什么还要创造出回归树这种学习算法呢?它相比于其他算法有和优点?
至于为什么,原因有很多,这里主要讲两点,这两点也是在我看来相比于其他算法最大的优点。
其一,决策树的算法思想与人类做决定时的思考方式很相似,它相比于其他算法,无需计算很多很多的各种参数,它能像人类一样综合各种考虑,做出很好的选择(不一定是最好啊ㄟ(▔,▔)ㄏ)。
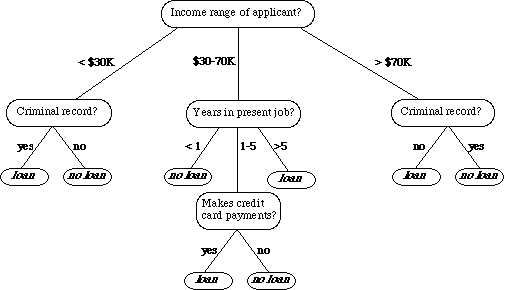
其二,它能将它做出决策的逻辑过程可视化(不同于SVM, NN, 或是神经网络等,对于用户而言是一个黑盒), 例如下图,就是一个银行是否给客户发放贷款使用决策树决策的一个过程。
三、What is the decision tree??
A decision tree is a tree where each node represents a feature(attribute), each link(branch) represents a decision(rule) and each leaf represents an outcome(categorical or continues value).
类似于下图中左边的数据,对于数据的分类我们使用右边的方式对其分类:
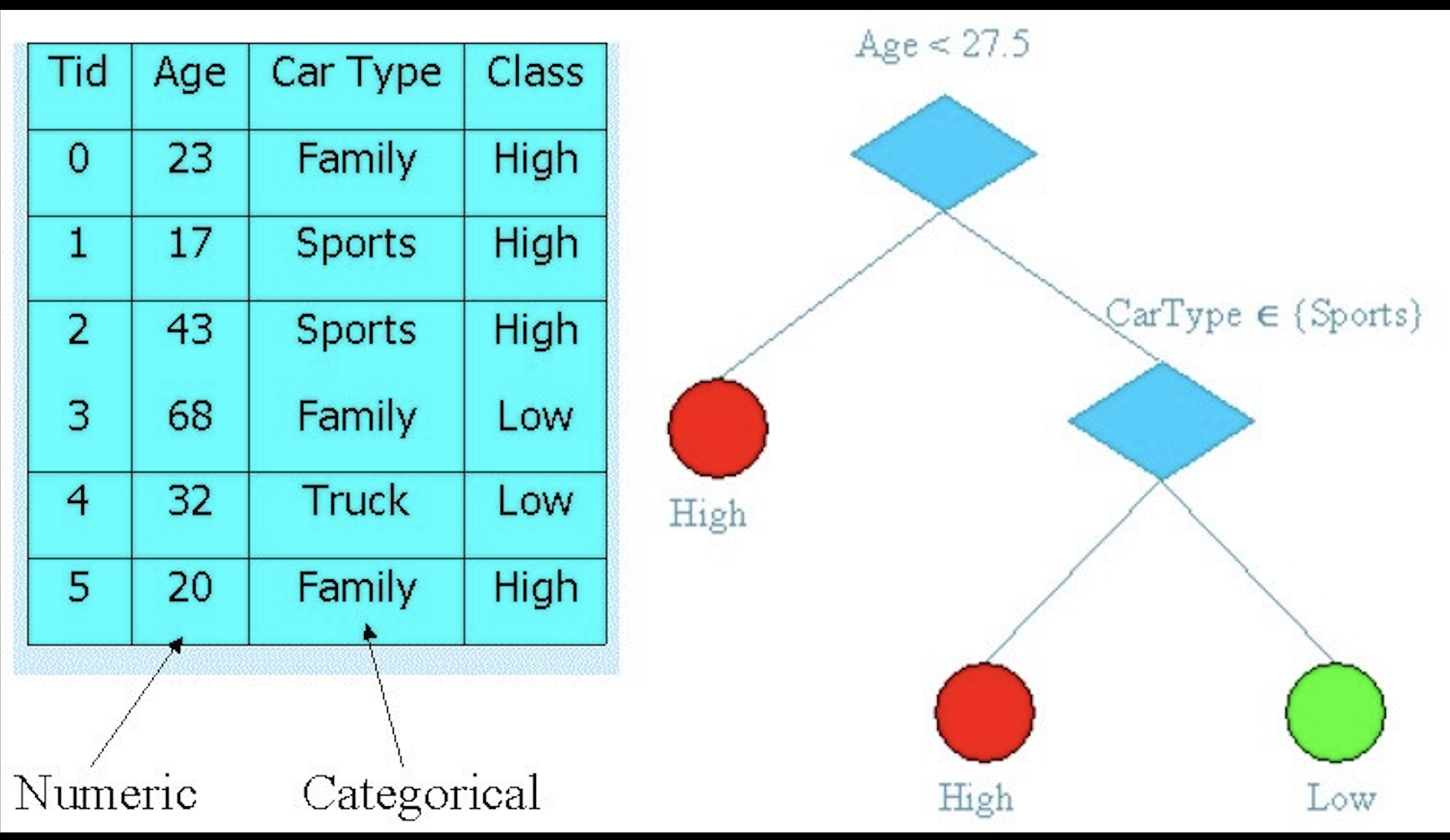
step 1:判断Age,Age<27.5,则Class=High;否则,执行step 2。
step 2: 判断CarType,CarType∈Sports,则Class=High;否则Class=Low。
对于一组数据,只需按照决策树的分支一步步的走下去,便可得到最终的结果,有点儿类似于程序设计中的多分支选择结构。
四、How to build this??
学习新知识,最主要的三个问题就是why,what,how。前两个问题已经在上面的介绍中解决了,接下来就是how,即如何建立一颗决策树?
建立决策树,有很多种算法,本文主要讲解一下两种:
- ID3 (Iterative Dichotomiser 3) → uses Entropy function and Information gain as metrics.
- CART (Classification and Regression Trees) → uses Gini Index(Classification) as metric.
————————————————————————————————————————————————————————————————————————————————————————————————————— 首先,我们使用第一种算法来对一个经典的分类问题建立决策树:
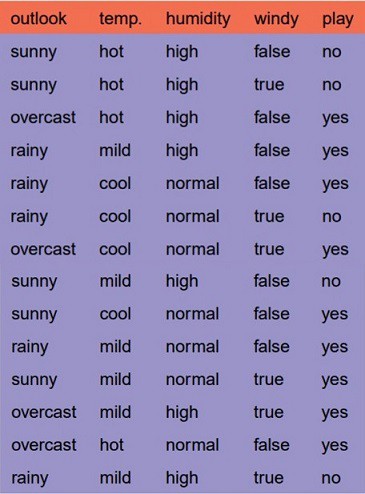
Let’s just take a famous dataset in the machine learning world which is whether dataset(playing game Y or N based on whether condition).
We have four X values (outlook,temp,humidity and windy) being categorical and one y value (play Y or N) also being categorical.
So we need to learn the mapping (what machine learning always does) between X and y.
This is a binary classification problem, lets build the tree using the ID3 algorithm.
首先,决策树,也是一棵树,在计算机科学中,树是一种数据结构,它有根节点(root node),分枝(branch),和叶子节点(leaf node)。
而对于一颗决策树,each node represents a feature(attribute),so first, we need to choose the root node from (outlook, temp, humidity, windy). 那么改如何选择呢?
Answer: Determine the attribute that best classifies the training data; use this attribute at the root of the tree. Repeat this process at for each branch.
这也就意味着,我们要对决策树的空间进行自顶向下的贪婪搜索。
所以问题又来了,how do we choose the best attribute?
Answer: use the attribute with the highest information gain in ID3.
In order to define information gain precisely, we begin by defining a measure commonly used in information theory, called entropy(熵) that characterizes the impurity of an arbitrary collection of examples.”
So what's the entropy? (下图是wikipedia给出的定义)

从上面的公式中我们可以得到,对于一个二分类问题,如果entropy=0,则要么全为正样本,要么全为负样本(即理论上样本应该属于两个,实际上所有的样本全属于一类)。如果entropy=1,则正负样本各占一半。
有了Entropy的概念,便可以定义Information gain:

有了上述两个概念,便可建立决策树了,步骤如下:
1.compute the entropy for data-set
2.for every attribute/feature:
1.calculate entropy for all categorical values
2.take average information entropy for the current attribute
3.calculate gain for the current attribute
3. pick the highest gain attribute.
4. Repeat until we get the tree we desired.
对于这个实例,我们来具体使用一下它:
step1(计算数据集整体的entropy):

step2(计算每一项feature的entropy and information gain):

这里只计算了两项,其他两项的计算方法类似。
step3 (选择Info gain最高的属性):
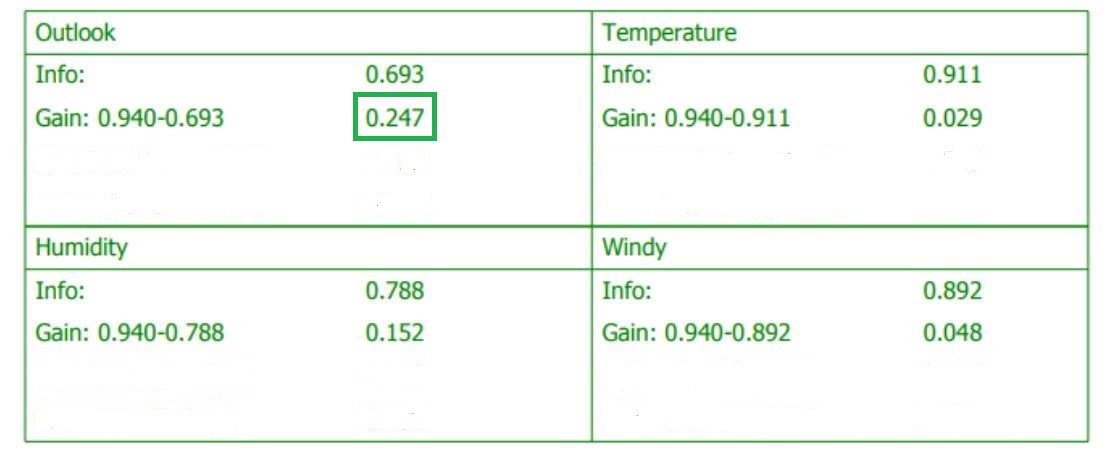
上表列出了每一项feature的entropy and information gain,我们可以发现Outlook便是我们要找的那个attribute。
So our root node is Outlook:
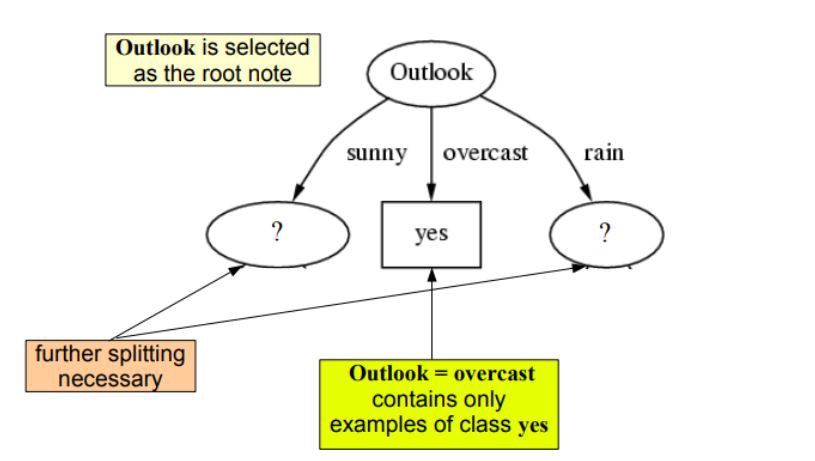
接着对于图中左边的未知节点,我们将由sunny得来的数据当做数据集,然后从这些数据中按照上述的步骤选择其他三个属性的一种作为此节点,对于右边的节点做类似操作即可:
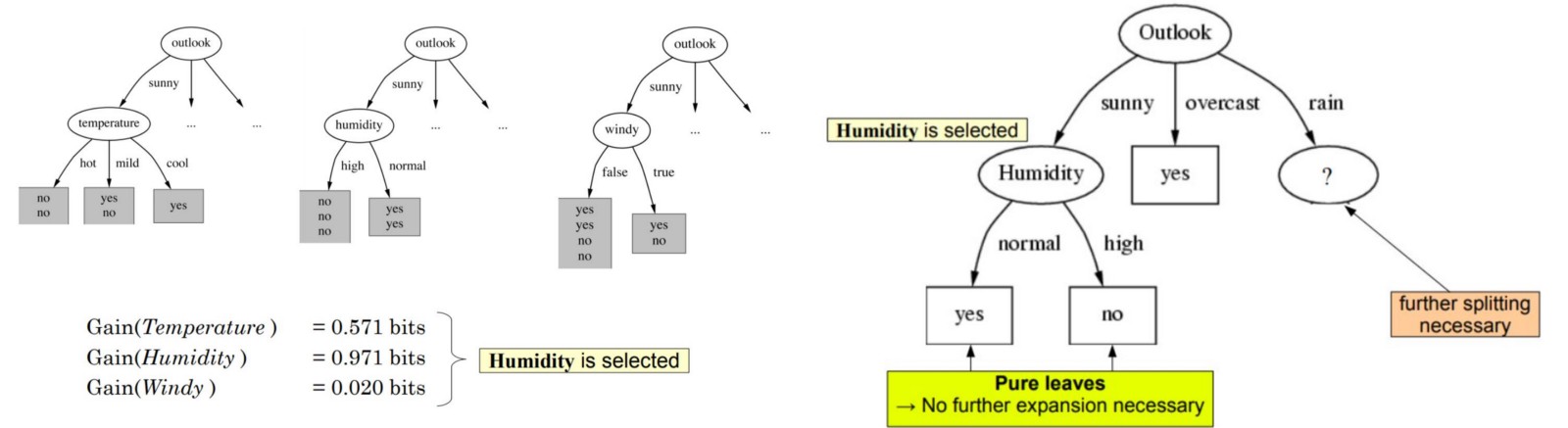
最终,建立的决策树如下:
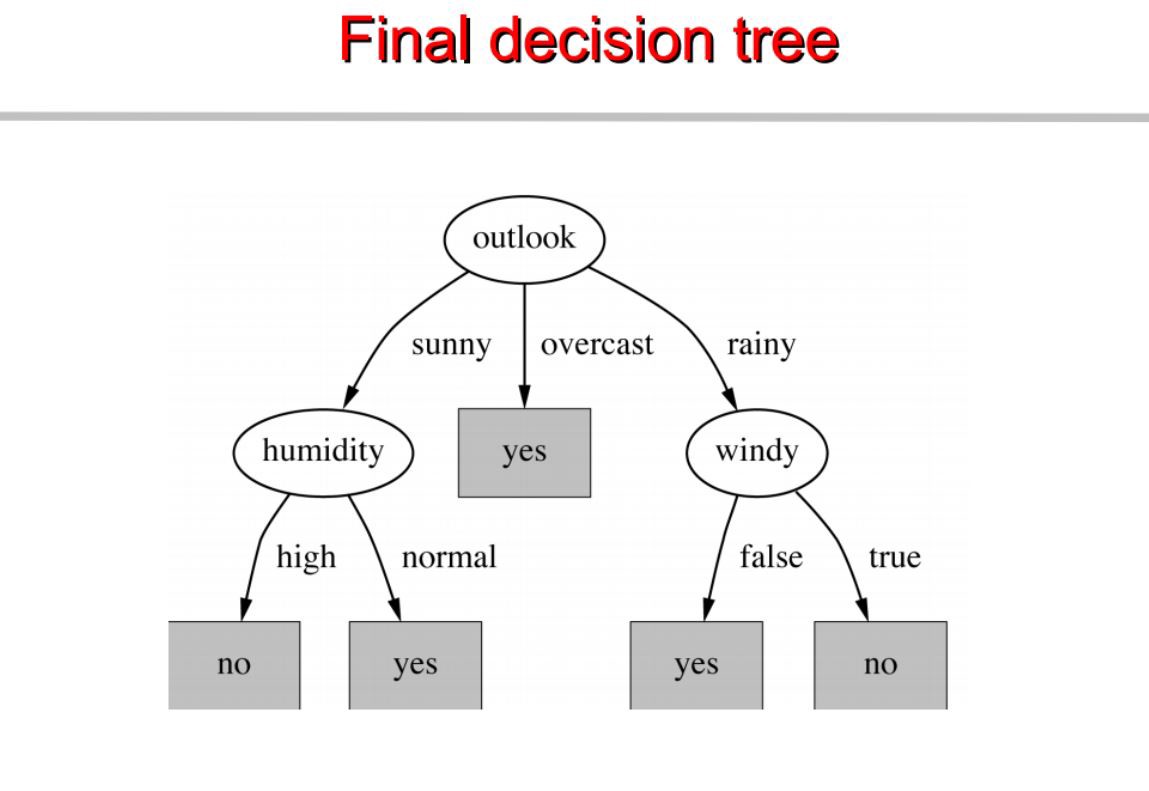
————————————————————————————————————————————————————————————————————————————————————————————————————— 接着,我们使用第二种算法来建立决策树(Classification with using the CART algorithm):
CART算法其实与ID3非常相像,只是每次选择时的指标不同,在ID3中我们使用entropy来计算Informaition gain,而在CART中,我们使用Gini index来计算Gini gain。
同样的,对于一个二分类问题而言(Yes or No),有四种组合:1 0 , 0 1 , 1 0 , 0 0,则存在
P(Target=1).P(Target=1) + P(Target=1).P(Target=0) + P(Target=0).P(Target=1) + P(Target=0).P(Target=0) = 1
P(Target=1).P(Target=0) + P(Target=0).P(Target=1) = 1 — P^2(Target=0) — P^2(Target=1)
那么,对于二分类问题的Gini index定义如下:

A Gini score gives an idea of how good a split is by how mixed the classes are in the two groups created by the split. A perfect separation results in a Gini score of 0, whereas the worst case split that results in 50/50 classes.
所以,对于一个二分类问题,最大的Gini index:
= 1 — (1/2)^2 — (1/2)^2
= 1–2*(1/2)^2
= 1- 2*(1/4)
= 1–0.5
= 0.5
和二分类类似,我们可以定义出多分类时Gini index的计算公式:
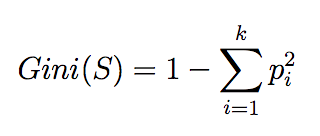
Maximum value of Gini Index could be when all target values are equally distributed.
同样的,当取最大的Gini index时,可以写为(一共有k类且每一类数量相等时): = 1–1/k
当所有样本属于同一类别时,Gini index为0。
此时我们就可以根据Gini gani来选择所需的node,Gini gani的计算公式(类似于information gain的计算)如下:
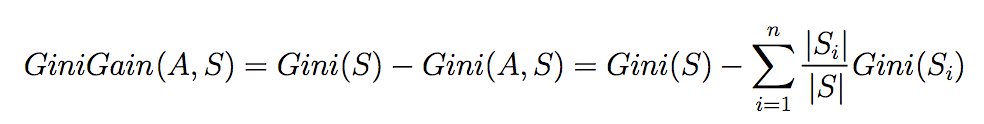
那么便可以使用类似于ID3的算法的思想建立decision tree,步骤如下:
1.compute the gini index for data-set 2.for every attribute/feature: 1.calculate gini index for all categorical values 2.take average information entropy(这里指GiniGain(A,S)的右半部分,跟ID3中的不同) for the current attribute
3.calculate the gini gain
3. pick the best gini gain attribute.
4. Repeat until we get the tree we desired.
最终,形成的decision tree如下:
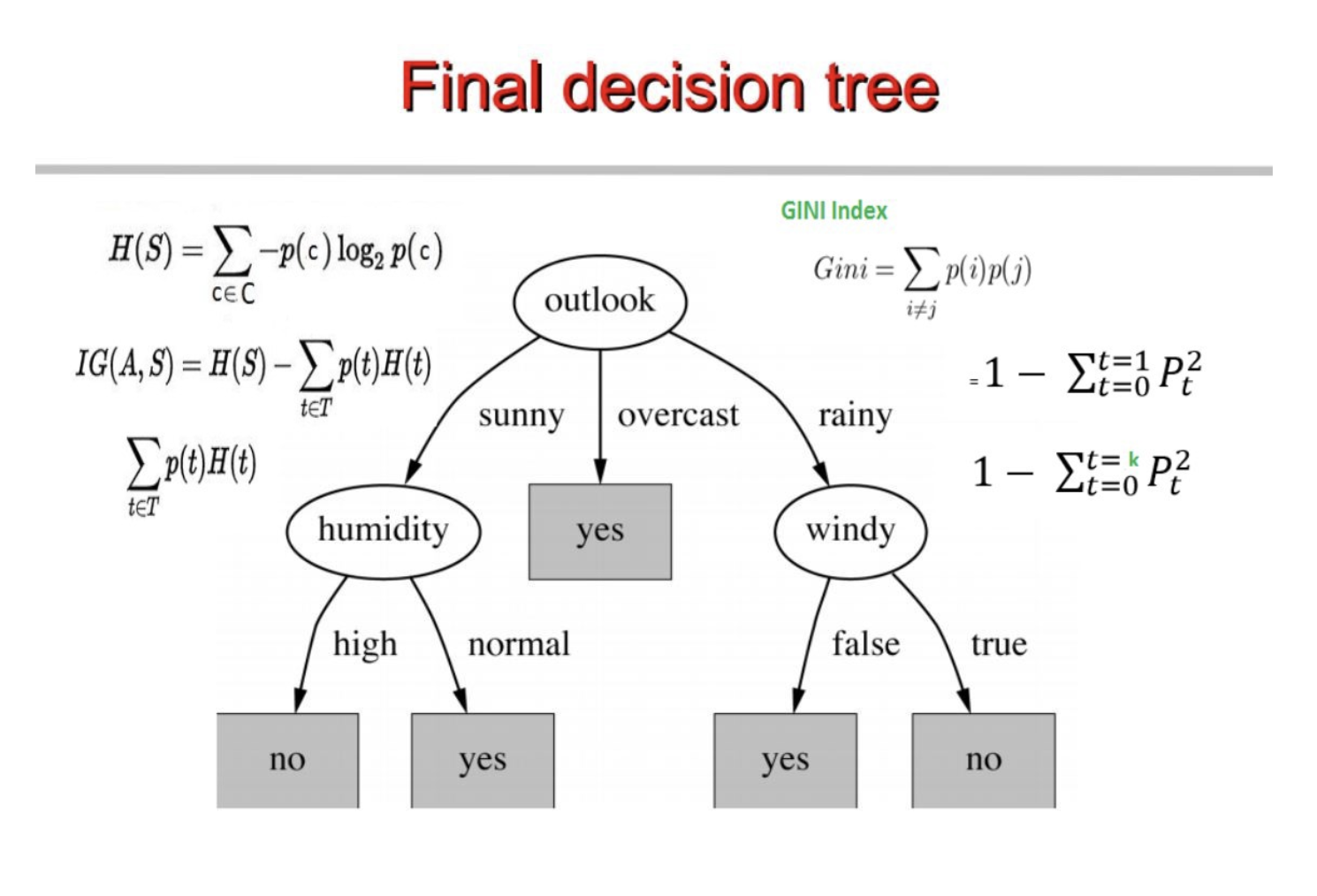
其实这两种算法本质没有任何区别,只是选择node时所用的指标(表达式)不同而已。




