SP26073 DIVCNT1 - Counting Divisors

贺了 x义x 和 🐟大 好多图

首先对这个问题做一个经典的转化：

\[\begin{aligned} \sum\limits_{i = 1} ^ n \sigma_0(i) &= \sum\limits_{i = 1} ^ n \lfloor \frac{n}{i} \rfloor\\ &= \sum\limits_{i = 1} ^ {n ^ {\frac{1}{2}}} \lfloor \frac{n}{i} \rfloor + \sum\limits_{i = n ^ {\frac{1}{2}} + 1} ^ n \sum\limits_{j = 1} ^ {\lfloor \frac{n}{i} \rfloor} 1\\ &= \sum\limits_{i = 1} ^ {n ^ {\frac{1}{2}}} \lfloor \frac{n}{i} \rfloor + \sum\limits_{i = 1} ^ {n ^ {\frac{1}{2}}} \sum\limits_{j = n ^ {\frac{1}{2}} + 1} ^ {\lfloor \frac{n}{i} \rfloor} 1\\ &= \sum\limits_{i = 1} ^ {n ^ {\frac{1}{2}}} \lfloor \frac{n}{i} \rfloor + \sum\limits_{i = 1} ^ {n ^ {\frac{1}{2}}} \left(\lfloor \frac{n}{i} \rfloor - n ^ {\frac{1}{2}}\right)\\ &= 2\sum\limits_{i = 1} ^ {n ^ {\frac{1}{2}}} \lfloor \frac{n}{i} \rfloor - \lfloor n ^ {\frac{1}{2}} \rfloor ^ 2 \end{aligned} \]

于是只需要考虑统计前者即可，再做一个组合意义上的转化：将 \(\lfloor \frac{n}{x} \rfloor\) 看作是 \(f(x) = \frac{n}{x}\) 在 \((i, f(i))\) 这个点到坐标轴之间的整点数量（不包括坐标轴，下同）

由于 \(f(x)\) 关于 \(y = x\) 对称，因此按照习惯再将上述组合意义 \(x, y\) 翻转，做一条 \(y = \lfloor n ^ {\frac{1}{2}} \rfloor\) 的直线，问题转化为求解下图 \(R\)（粉色）区域内的整点数量：

直接做曲线围成区域内的整点不好做，但根据 pick 定理利用面积我们可以求简单多边形内的整点数量，于是考虑化曲为直。

具体地，发现 \(f(x)\) 为凸函数，那么可以考虑在 \(R'\)（绿色）区域内建立一个凸包，那么凸包以外在 \(y = \lfloor n ^ {\frac{1}{2}} \rfloor\) 以下的点都在 \(R\) 区域内，比如如下图所示（三角形为了演示凸包外不存在 \(R'\) 内的点，注意 \(f(x)\) 上的整点在 \(R\) 内）。

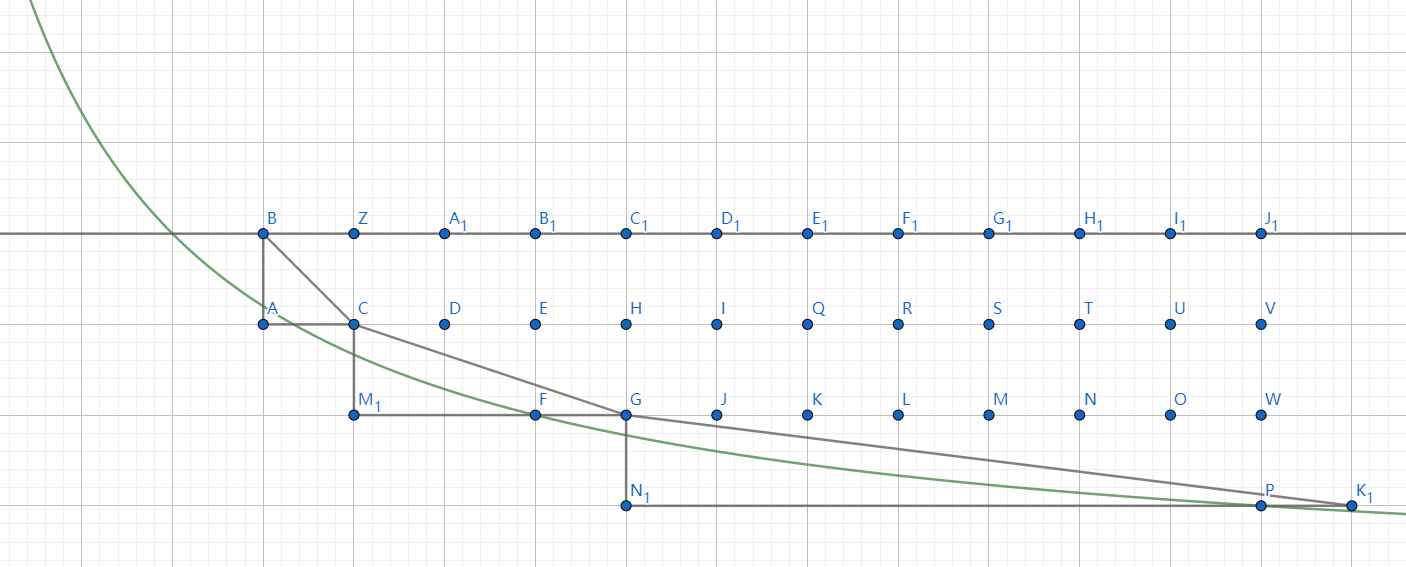
建出这个凸包以后，就可以沿着凸包从左至右将 \(R\) 内的的整点贡献加上。

具体地，假设凸包上相邻两点 \(A(x, y), B(x + u, y - v)\) 那么贡献就应该是：

• 首先加上左侧整个矩形内的整点数量 \(xv\) 注意上边界上的点上一轮计算过，左边界在坐标轴上不能计算。

• 首先 \(AB\) 上的整点数量（除端点）有：\((u, v) - 1\)，根据皮克定理，三角形总共的点数为 \(\frac{1}{2}(uv + u + v + 1 + (u, v) - 1) = \frac{1}{2}(uv + u + v + (u, v))\)，再减去左边界上算过的点，共 \(\frac{1}{2}(uv + u - v + (u, v)) - 1\).

综上，一条凸包上的边贡献为 \(xv + \frac{1}{2}(uv + u - v + (u, v)) - 1\)，特别地，第一条边需要算上上边界，那么不妨从上图 \(B\) 点左上角哪个点 \(P_0:(\frac{n}{\lfloor n ^ {\frac{1}{2}} \rfloor}, \lfloor n ^ {\frac{1}{2}} \rfloor + 1)\) 开始就可以保持统一性了。

那么就只需要想办法把凸包建出来即可。

从 \(P_0\) 开始，我们需要找到一个向量 \(\vec{c} = (u, v)\) 使得 \(P_0 + \vec{c}\) 在 \(f\) 上方且不存在一个斜率更小的 \(\vec{c'}\) 使得 \(P_0 + \vec{c'}\) 也在图像上方，同时为了方便钦定 \((u, v) = 1\)，那么此时凸包上每条边的贡献就是 \(xv + \frac{1}{2}(u - 1)(v + 1)\).

考虑按照 \(\vec{c}\) 的斜率进行二分，直接二分实数不好对应整数 \(u, v\)，因此可以考虑直接在 stern-brocot tree 上二分。

初始我们加入 \((1, 0), (1, 1)\) 两个分数（为了方便记录绝对值，且可知本题凸包上所有直线斜率绝对值不大于 \(1\)），然后直接在 SBT 上二分找到这样一个向量 \(\vec{c}\).

初始左端点 \(\vec{l_0} = (1, 1)\) 右端点 \(\vec{r_0}(1, 0)\)（下面加法都带符号，即 \(y\) 方向是减），分以下几种情况讨论：

• 若中间向量 \(\vec{mid}\) 使得 \(P_0 + \vec{mid}\) 在 \(f\) 上方，那么就可以将右端点收缩到 \(mid\).
• 否则，将左端点收缩到 \(\vec{mid}\).

考虑一下什么时候退出二分。

如果有 \(\frac{-r_y}{r_x} \le f'(P_{0_{x}} + mid_x)\)，那么接下来无论如何都会在 \(f\) 下方，因为就算是不断加 \(\vec{r}\) 每次 \(y\) 方向的减少量也多于 \(f\) 在 \(y\) 方向上的减少量。

由于凸包上的线是有限的，因此在有限次二分后也一定会推出二分。

那么最后就可以在 \(P_0\) 移动到 \(P_0 + \vec{r}\) 这条边就一定会在凸包上，然后就可以继续往下迭代了。

但这样复杂度其实很劣，因为每次都要从 \((1, 0), (1, 1)\) 这两个向量开始二分，考虑减去一部分不必要的二分。

我们每次往下迭代的时候，首先不断加上 \(\vec{r}\) 直到终点在 \(f\) 以下，这里新加上 \(\vec{r}\) 的部分也是在凸包上的，根据凸包的性质可以保证正确性。

然后我们将每次二分中右端点移动的 \(\vec{mid}\) 按照斜率单调递减依次加入一个单调栈，这个在二分过程中很好维护。

接下来从栈顶开始不断弹栈（可以用凸包性质证明两个弹掉的向量之间不可能存在接下来凸包上的边），直到 \(P_0\) 加上栈顶在 \(f\) 上停止，此时栈顶向量记作 \(l_0\)，最后一个被弹掉的向量记作 \(r_0\)，然后以 \(l_0, r_0\) 为左右端点二分寻找下一条凸包上的边。

本质上就是将 SBT 分成了几个可能出现凸包上边的子树，然后每次清除一些不可能的子树，再不断划分子树的过程。

可以理性感觉上述划分的子树数量不大，可以分析得复杂度是 \(\mathcal{O}(n ^ {\frac{1}{3}}\log n)\) 的，但是我不会。