AtCoder AGC002 简要题解
从今天开始,联赛之前大约要完成前 \(20\) 套 \(\rm AGC\),希望不要鸽。
A
略
B
感觉这题比 \(\rm C\) 题难。
考虑对于每个时刻维护每个位置是否可能出现红球,那么一个时刻一条边只会影响到两个位置。
那么一路维护过来即可,复杂度 \(\mathcal{O}(n)\)。
C
显然最终一定会存在一个时刻使得有一对相邻点 \((i, i + 1)\) 所在的绳子上只存在 \((i, i + 1)\) 之间这一条边。
那么原问题存在一组解的必要条件就是 \(\max\limits_{i = 1} ^ {n - 1} a_i + a_{i + 1} \ge L\)。
然后我们令满足上述条件的一个位置为 \(x\),那么只需要把 \(x\) 左侧的绳结从左至右依次删除,然后再从右往左把 \(x\) 右侧的绳结依次删除最后删 \(x\) 即可。
那么上面哪个必要条件就是充要条件,构造可以按照上述方法构造。
D
我只会两个 \(\log\) 的做法,然后赛后补题解发现可以一个 \(\log\)。
两个 \(\log\) 的话有两种做法:
二分答案,考虑如何 \(\rm check\)。
考虑建出 \(\rm Kruskal\) 重构树,在树上倍增讨论一下就可以得到可以到达的点数了。
直接整体二分,显然一次询问可以用并查集解决。
整体二分的时候考虑先把左区间的边加上,然后先递归右区间,右区间递归完上来之后用可撤销并查集撤销左区间的边然后递归左区间。
一个 \(\log\) 个的话考虑离线二分。
这样子就不需要支持可撤销了,那么复杂度就是 \(\mathcal{O}(n \alpha(n) \log n)\)。
E
貌似毫无思路,不妨尝试寻找一些性质:
- 假设操作一选择了 \(x\) 个元素,那么这 \(x\) 个元素不会因为操作而改变,一定会是最大的前 \(x\) 个元素(有相同的随便取)。
因此,有效的局面本质上很少,因为我们只关心当前做了几次操作一还是操作二,不论顺序如何最终局面相同。
分析一下上界,不难发现为:\(\mathcal{O}(\sum a_i)\),考虑进一步优化这个做法。
根据转移的特性,我们不妨将问题转化为如下模型:
首先将所有元素从大至小排序,然后将其抽象为 \(n\) 个由 \(1 \times 1\) 方格构成的柱子,那么双方的一种决策路径可以看作是 左下角每次向右或向上走到边界的过程, 如下图所示(图蒯的官方的)。

那么我们手玩一下每个点的胜负性可以发现,这个格点图上 边界全为必胜,\(x + y\) 对角线上的格点胜负性相同。
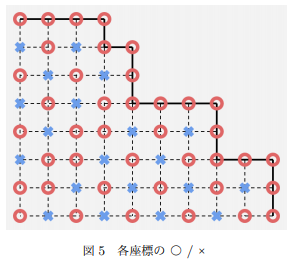
其中 O 表示必胜格点,X 表示必败节点。
有了这个性质我们就可以利用左下角所在对角线上的任意元素确定最终初始局面的胜负性了。
不难发现可以选取所在对角线最靠右在碰到边界前的第最后一个格点,这样就只用关心该点到上面,右边第一个边界的距离的奇偶性了:只要存在一个距离为奇数那么就必胜否则必败(就像下图所示)。
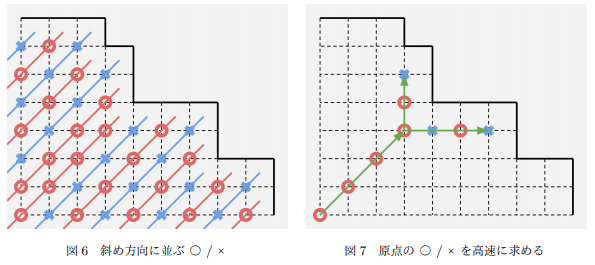
复杂度 \(\mathcal{O}(n \log n)\),瓶颈在于排序。
F
下文颜色种类数为 \(m\),每种颜色有 \(n\) 个球。
考虑什么样的序列是合法的,当且仅当对于每个前缀出现的有颜色的球的种类数不大于白色球的数量。
由于每种球之间有标号,而每种球内部之间无标号,因此这本质上是一个类排列计数问题。
难处理的地方在于所有颜色第一个出现的球的位置需要被染成白色,而白色内部也是无标号的。
常见的方法是我们考虑将合法序列和没有染白色的序列构造一种双射,来计算在某种要求之下的没有染白色的序列。
下文称没有被染成白色的序列为原始序列。
不难发现可以将合法序列的每个白色球归进其后面第一个之前没有归进其他白色球且最靠前的颜色。
容易证明这样可以构成双射。
考虑将这个对原始序列的限制进行转化,我们将白色球的位置和它归入的颜色中最靠前的球连边。
不难发现这样的连边不存在包含关系,只存在相离或相交关系。
那么对应原始序列就相当于对每种颜色第一次出现的位置和第二次出现的位置的要求:
- 将每种颜色第一次出现的位置依次写下记为 \(A\),第二次出现的位置依次写下记为 \(B\),那么这样的原始序列合法当且仅当 \(A, B\) 离散化之后的序列完全相同!
有了这个性质之后我们不难得到一个暴力 \(\rm dp\),我们钦定按照每种颜色第一次出现的顺序来插入每种元素。
那么可以考虑每次往当前得到的序列当中插入一种新的颜色(\(n\) 个球一次性插入),只需要保证第一个位置再上一种颜色第一个位置之后,第二个位置在上一种颜色第二个位置之后即可。
于是可以令 \(f_{i, j, k}\) 表示当前考虑到第 \(i\) 中颜色,当前颜色第一个出现的位置在 \(j\),第二次出现的位置在 \(k(j < k)\) 的方案,那么不难得到转移:
使用前缀和优化,复杂度 \(\mathcal{O}(n ^ 2m ^ 3)\),状态优化不下去,考虑换一种 \(\rm dp\) 方式。
注意到我们只关注每种颜色第一个位置和第二个位置的相对位置,而两者的关联性并不大,于是可以考虑将每种元素第一个位置的决策和第二个位置的决策分开考虑,这样就能降下维度了。
于此同时,我们现在考虑先不急着将白球归入某种颜色,等到后面加入了某种没有匹配白球的颜色时再将最前面的白球归入该种颜色,这样依然满足双射的构造。
由于我们不能记录序列中白球的位置,那么就可以考虑直接在 \(n \times m\) 个空位中填数,这样如果按照钦定的颜色第一次 / 第二次出现顺序插入,就只需要保证每次插入的白球 / 颜色段的第一个元素在当前的第一个空位即可。
于是可以直接令 \(f_{i, j}\) 表示当前已经插入了 \(i\) 个白球,\(j(i \ge j)\) 个颜色段的方案,那么有转移:
线性预处理阶乘及其逆元,复杂度 \(\mathcal{O}(nm)\)。




