CF1278E Tests for problem D
不难发现为了逐步确定每个点于其相邻点的相交情况,那么我们只可能有两种逐步构造的方式:从根开始往下构造,以及从子树往根上构造。经过很久的尝试,我发现从根往下构造是一件很困难的事情,于是我们可以反过来考虑第二种构造方式。
既然是从子树开始构造,那么我们先想一下最底层是如何构造的。不难发现最底层实质上是一个菊花图的形式,因为父亲和这些儿子必然有交,那么这些儿子之间一定也会有交,为了让儿子之间不会互相连边,我们只能让所有儿子区间一个包含另一个。为了方便起见,我们让所有儿子的区间和父亲区间的交在左端点,大致如下图所示:
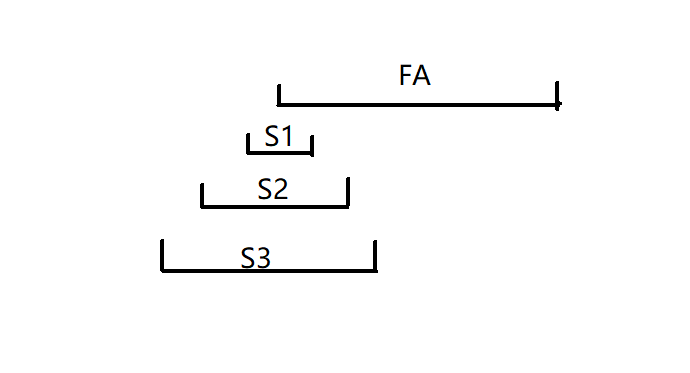
下面继续考虑如何将子树合并。不难发现为了让子树之间不会互相连边,一个最简单的方法就是将不同子树内的点分割开来,但因为所有儿子还是要与父亲连边,因此我们还需将所有儿子构造成上面那种菊花图的形式,具体地大致如下图所示:
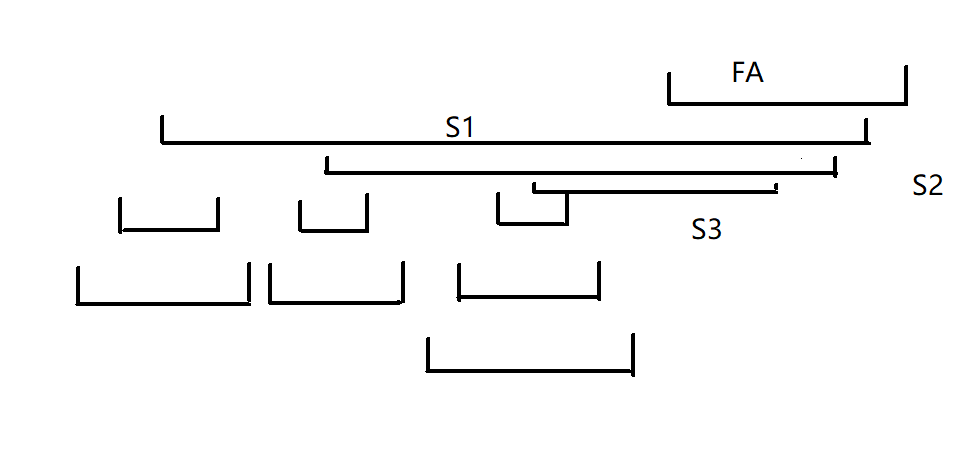
不难发现这样刚好用到的点数为 \(2n\) 个,具体实现时从根往儿子递归,传入当前子树内能使用的区间范围即可。
#include <bits/stdc++.h>
using namespace std;
#define rep(i, l, r) for (int i = l; i <= r; ++i)
#define Next(i, u) for (int i = h[u]; i; i = e[i].next)
const int N = 500000 + 5;
struct edge {
int v, next;
}e[N << 1];
int n, u, v, tot, h[N], l[N], r[N], s[N], sz[N];
int read() {
char c; int x = 0, f = 1;
c = getchar();
while (c > '9' || c < '0') { if(c == '-') f = -1; c = getchar();}
while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
void add(int u, int v) {
e[++tot].v = v, e[tot].next = h[u], h[u] = tot;
e[++tot].v = u, e[tot].next = h[v], h[v] = tot;
}
void Prefix(int u, int fa) {
s[u] = 1;
Next(i, u) if(e[i].v != fa) Prefix(e[i].v, u), s[u] += s[e[i].v];
}
void dfs(int u, int fa, int L, int R) {
int ch = 0; sz[u] = 1;
Next(i, u) {
int v = e[i].v; if(v == fa) continue;
++ch, dfs(v, u, L + 2 * sz[u] - ch - 1, L + 2 * sz[u] - ch + 2 * (s[v] - 1));
r[v] = R - ch, sz[u] += sz[v];
}
l[u] = R - ch - 1; if(u == 1) r[u] = R;
}
int main() {
n = read();
rep(i, 1, n - 1) u = read(), v = read(), add(u, v);
Prefix(1, 0), dfs(1, 0, 1, 2 * n);
rep(i, 1, n) printf("%d %d\n", l[i], r[i]);
return 0;
}



