Atcoder ARC-060
ARC060(2020.7.8)
A
背包板子
B
首先感觉这个东西应该不能直接 \(O(1)\) 算出来,那么复杂度应该就是 \(O(\log n), O(\sqrt{n}), O(\sqrt{n} \log n)\) 之类的,看数据范围可以猜到应该不是 \(O(\log n)\) 的(其实是不知道怎么做)。于是按照套路我们考虑根号分治,可以考虑枚举这个 \(b\),那么对于 \(b \le \sqrt{n}\) 的部分,直接枚举即可,再 \(O(\log n)\) 判断。然后我们可以发现对于 \(b > \sqrt{n}\) 的部分,因为 \(b ^ 2 > n\) 那么 \(n\) 在 \(b\) 进制下最多只有两位,那么不妨设 \(pb + q = n\) 则 \(p + q = s\) 两式相减可得,\(p(b - 1) = n - s\),则 \(b - 1 \mid n - s\) 于是可以考虑枚举 \(n - s\) 小于 \(\sqrt{n - s}\) 的约数 \(d\) 那么 \(b - 1 = \frac{n - s}{d}\) 这一部分的复杂度同样是 \(O(\sqrt{n} \log n)\) 的,因此总复杂度 \(O(\sqrt{n} \log n)\).
C
可以发现我们可以预处理出每个点再一天内往后最远能到达的点,于是问题就变成问从一个点最少往后跳几次能跳过另一个点,那么我们可以直接分块处理,预处理出一个点走出块内第一个点需要的最短跳跃次数,于是查询只需要跳块即可。那么复杂度就可以做到 \(O(n \sqrt{n})\) 了,那么还有没有更优秀的做法呢?实际上是有的,可以考虑倍增,那么类似于求 \(\rm LCA\) 的倍增方式跳到下标小于另一个点的第一个点,次数 \(+1\) 即是答案。
D
首先有一些特殊情况,首先如果原串是不循环的,那么答案就是 \(1, 1\),其次如果原串中的每个元素都相同,那么答案就是 \(n, 1\),对于剩下的情况,我认为将原循环串去掉最后一位剩下的串不可能是一个循环串,于是我大胆地猜测第一问的答案是 \(2\),结果还猜对了。下面是一个关于字符串循环节很关键的一个性质:
给定两个正整数 \(p, q\) 如果一个长度不小于 \(p + q - \gcd(p, q)\) 的串 \(S\) 中存在长度为 \(p, q\) 的循环节,那么 \(\gcd(p, q)\) 也是 \(S\) 的循环节。
考虑将循环的意义用数学语言表达下来,不难发现对于 \(\forall i \in [1, n]\) 有 \(S_i = S_{i + p} = S_{i + q} = S_{i + px + qy}\),根据裴蜀定理考虑到 \(px + qy = \gcd(p, q)\) 是一定有解的,那么就会有 \(S_i = S_{i + \gcd(p, q)}\) 也就意味着 \(\gcd(p, q)\) 也是一个循环节。
那么我们将原串去掉最后一位之后假设剩下的串最小循环节长度为 \(x\),原串最小循环节长度为 \(y\),因为 \(\gcd(n - 1, n) = 1\) 因此 \(n - 1, n\) 不会包含相同约数,因此 \(\gcd(x, y) = 1\),那么根据上面的性质,将原串继续按照循环节延长,那么 \(1 \sim x \times y\) 这一段子串就一定会含有 \(x, y\) 两种循环节,那么 \(gcd(x, y) = 1\) 也会是一种循环节,因此原串中每一个字符都将相等与条件矛盾。
那么下面我们就只需要枚举中间的断点,判断左右是否都是不循环的即可。接下来又是一个非常重要的结论,一个字符串存在循环节的充要条件是 \(\exist x \mid n, S_{1, n - x} = S_{x + 1, n}\)
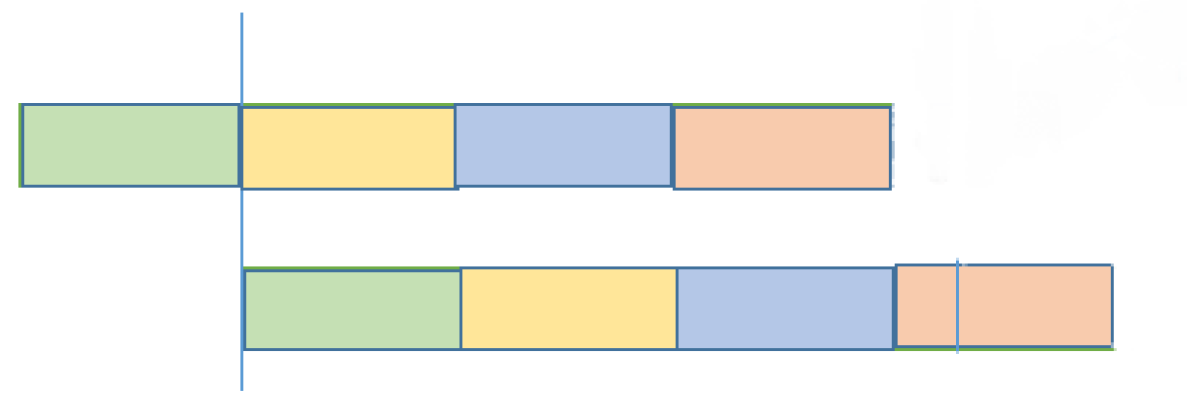
首先假设 \(S_{1, x}\) 是上图中的绿色部分,其他颜色分别是长度为 \(x\) 的块,因为 \(S_{1, n - x} = S_{x + 1, n}\) 那么相同颜色块应该相同,又根据在原串中的位置可以得到绿色块和黄色块相同,同理又可以得到黄色块和红色块相同,以此类推可以得到原串是个循环串。
得到循环串的判定条件后我们发现需要枚举这个长度 \(x\),又因为 \(x \mid n\) 那么我们可以枚举 \(n\) 的约数,事实上因为我们需要知道的是前缀是否是循环的,那么第一个循环节都会是从 \(1\) 开始的,那么我们枚举第一个循环节的长度,那么能以该长度作为循环节的只有其倍数,那么我们再枚举一下其倍数 \(\rm Hash\) 一下就可以 \(O(1)\) 判断了,后缀也是类似的。那么最终统计答案就非常简单了。
可以发现上面那个做法的复杂度是 \(O(n \ln n)\) 的,那么能不能做到 \(O(n)\) 呢?事实上是可以的,需要使用到 \(kmp\) 的性质。
首先我们可以将判断是否循环的条件改成 \(n - nxt_{n} \mid n\)。首先我们可以知道如果 \(n - nxt_{n} \mid n\) 那么是一定有循环节的,类似上面的证明。下面来证明对于 \(n - nxt_{n} \nmid n\) 的情况不存在循环节。
首先考虑 \(nxt\) 数组的定义,不难发现有 \(S_{1, nxt_n} = S_{n - nxt_n + 1, n}\),那么类似于第一种做法循环节的证明方法,可以发现 \(S_{1, n - nxt_n}\) 也可以在原串中循环只是不能刚好循环完毕,即最后一次循环只能出现部分。我们称这种循环节为伪循环节。
首先令 \(x = n - nxt_n\),假设存在一个长度为 \(len\) 的循环节,显然 \(len \ne x\)。首先如果 \(len < x\),那么显然 \(nxt_n\) 可以变大,矛盾。如果 \(x \mid len\) 既然 \(len\) 都能循环那么 \(x\) 一样能循环,矛盾。对于 \(x \nmid len\) 的情况,因为 \(x \nmid len\) 那么一定存在一个伪循环节会跨过第一个循环节和第二个循环节,假设这个伪循环节是第 \(k\) 个,那么 \(S_{len + 1, len + x} = S_{1, x} = S_{k \times x + 1, (k + 1) \times x}\) 可以发现 \(S_{len + 1, len + x}, S_{k \times x + 1, (k + 1) \times x}\) 重叠了一段区间且长度相同,那么 \(S_{len + 1, k \times x}\) 就可以作为一段新的伪循环节,且长度小于 \(x\),那么 \(nxt_n\) 一样可以变大,矛盾。
那么我们 \(kmp\) 可以求出每个位置的 \(nxt\) 值,前缀后缀判断是可以 \(O(1)\) 做到的,因此总复杂度 \(O(n)\).
实际上循环节还有一个很奇妙的性质,即所有循环节长度都是最小循环节长度的倍数。假设存在两个个长度为 \(p, q(\gcd(p, q) \ne p)\) 的循环节,\(p\) 为长度最小的循环节。那么显然有 \(\gcd(p, q) < p\),根据最开始的那条性质,\(\gcd(p, q)\) 也是一个循环节,那么最小循环节的长度就会是 \(\gcd(p, q)\) 而不是 \(p\),矛盾。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号