P1407 [国家集训队] 稳定婚姻

[国家集训队] 稳定婚姻

题目描述

我们已知 $n$ 对夫妻的婚姻状况，称第 $i$ 对夫妻的男方为 $B_i$，女方为 $G_i$。若某男 $B_i$ 与某女 $G_j$ 曾经交往过（无论是大学，高中，亦或是幼儿园阶段，$i \le j$），则当某方与其配偶（即 $B_i$ 与 $G_i$ 或 $B_j$ 与 $G_j$）感情出现问题时，他们有私奔的可能性。不妨设 $B_i$ 和其配偶 $G_i$ 感情不和，于是 $B_i$ 和 $G_j$ 旧情复燃，进而 $B_j$ 因被戴绿帽而感到不爽，联系上了他的初恋情人 $G_k$ ……一串串的离婚事件像多米诺骨牌一般接踵而至。若在 $B_i$ 和 $G_i$ 离婚的前提下，这 $2n$ 个人最终依然能够结合成 $n$ 对情侣，那么我们称婚姻 $i$ 为不安全的，否则婚姻 $i$ 就是安全的。

给定所需信息，你的任务是判断每对婚姻是否安全。

输入格式

第一行为一个正整数 $n$，表示夫妻的对数；

以下 $n$ 行，每行包含两个字符串，表示这 $n$ 对夫妻的姓名（先女后男），由一个空格隔开；

第 $n+2$ 行包含一个正整数 $m$，表示曾经相互喜欢过的情侣对数；

以下 $m$ 行，每行包含两个字符串，表示这 $m$ 对相互喜欢过的情侣姓名（先女后男），由一个空格隔开。

输出格式

输出文件共包含 $n$ 行，第 $i$ 行为 Safe（如果婚姻 $i$ 是安全的）或 Unsafe（如果婚姻 $i$ 是不安全的）。

样例 #1

样例输入 #1

2
Melanie Ashley
Scarlett Charles
1
Scarlett Ashley

样例输出 #1

Safe
Safe

样例 #2

样例输入 #2

2
Melanie Ashley
Scarlett Charles
2
Scarlett Ashley
Melanie Charles

样例输出 #2

Unsafe
Unsafe

提示

对于 $20\%$ 的数据，$n \le 20$；

对于 $40\%$ 的数据，$n \le 100$，$m \le 400$；

对于 $100\%$ 的数据，所有姓名字符串中只包含英文大小写字母，大小写敏感，长度不大于 $8$，保证每对关系只在输入文件中出现一次，输入文件的最后 $m$ 行不会出现未在之前出现过的姓名，这 $2n$ 个人的姓名各不相同，$1 \le n \le 4000$，$0 \le m \le 20000$。

分析

对于n对夫妻 $(u,v)$ 和m对前情侣 $(u',v')$ ，建边 $u->v$ 和 $v'->u'$ 。

跑一边Tarjan缩点，如果 $(u,v)$ 在一个SCC中则不安全。因为此时 $(u,v)$ 在长度大于3的偶环上，可以使得 $(u,v')$ 和 $(v,u')$ 配对。

如图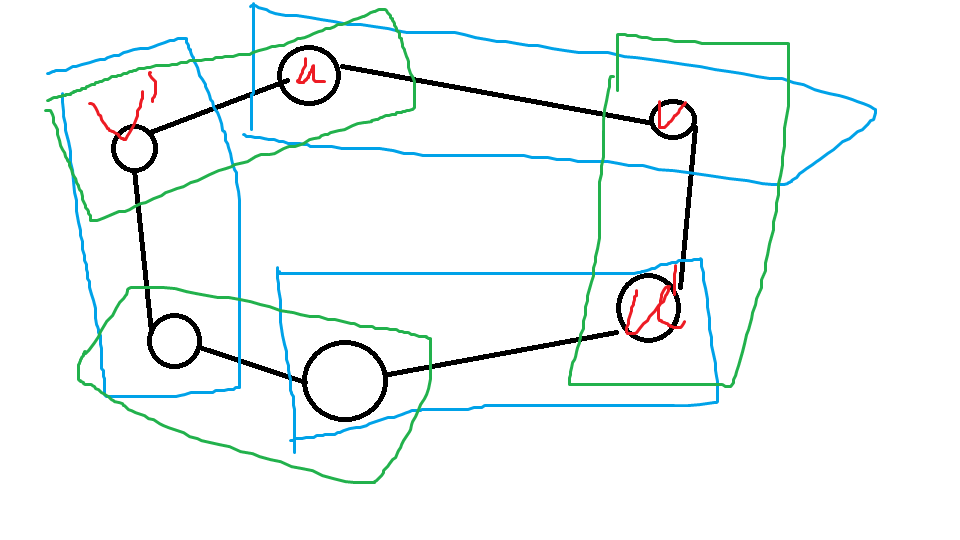

#include<bits/stdc++.h>
using namespace std;
const int N=2e4+100,M=1e5+100;
int n,m;
int head[N],cnt;
int dfn[N],low[N],tot,dd;
int sta[N],top,id,scc[N];
int pa[N][2];
bool inc[N];
map<string,int>mp;
struct edge{int y,n;}e[M<<1];
string s1,s2;
void ad(int x,int y)
{
    e[++cnt].n=head[x];
    e[cnt].y=y;
    head[x]=cnt;
}
 
void go(int u)
{
    sta[++top]=u;
    inc[u]=1;
    low[u]=dfn[u]=++tot;
    for(int i=head[u];i;i=e[i].n)
    {
        int v=e[i].y;
        if(!dfn[v])
        {
            go(v);
            low[u]=min(low[u],low[v]);
        }
        else if(inc[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u])
    {
        ++id;
        while(sta[top]!=u)
        {
            scc[sta[top]]=id;
            inc[sta[top]]=0;
            --top;
        }
        scc[u]=id;
        inc[u]=0;
        --top;
    }
}
 
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
        cin>>s1>>s2;
        int id1=mp[s1],id2=mp[s2];
        if(!id1)id1=mp[s1]=++dd;
        if(!id2)id2=mp[s2]=++dd;
        pa[i][0]=id1;
        pa[i][1]=id2;
        ad(id1,id2);
 
    }
    scanf("%d",&m);
    for(int i=1;i<=m;++i)
    {
        cin>>s1>>s2;
        int x=mp[s2],y=mp[s1];
        ad(x,y);
    }
    for(int i=1;i<=dd;++i)
        if(!dfn[i])go(i);
    for(int i=1;i<=n;++i)
    {
        if(scc[pa[i][0]]==scc[pa[i][1]])printf("Unsafe");
        else printf("Safe");
        putchar('\n');
    }
    return 0;
}