BZOJ3157/BZOJ3516 国王奇遇记（矩阵快速幂/数学）

　　由二项式定理，(m+1)^k=ΣC(k,i)*mⁱ。由此可以构造矩阵转移，将mⁱ*i^k全部塞进去即可，系数即为组合数*m。复杂度O(m³logn)，因为大常数喜闻乐见的T掉了。

#include<iostream> 
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
    int x=0,f=1;char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
    while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return x*f;
}
#define N 202
#define P 1000000007
int n,m,C[N][N];
struct matrix
{
    int n,a[N][N];
    matrix operator *(const matrix&b) const
    {
        matrix c;c.n=n;memset(c.a,0,sizeof(c.a));
        for (register int i=0;i<n;i++)
            for (register int j=0;j<N;j++)
                for (register int k=0;k<N;k++)
                c.a[i][j]=(c.a[i][j]+1ll*a[i][k]*b.a[k][j]%P)%P;
        return c;
    }
}f,a;
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj3157.in","r",stdin);
    freopen("bzoj3157.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    n=read()+1,m=read();
    C[0][0]=1;
    for (int i=1;i<=m;i++)
    {
        C[i][0]=C[i][i]=1;
        for (int j=1;j<i;j++)
        C[i][j]=(C[i-1][j-1]+C[i-1][j])%P;
    }
    a.n=m+2;
    for (int i=0;i<=m;i++)
        for (int j=0;j<=i;j++)
        a.a[j][i]=1ll*m*C[i][j]%P;
    a.a[m][m+1]=a.a[m+1][m+1]=1;
    f.n=1;f.a[0][0]=1;
    for (;n;n>>=1,a=a*a) if (n&1) f=f*a;
    cout<<f.a[0][m+1];
    return 0;
}

 

　　考虑更神的完全想不到的推导：（直接搬了）

　　

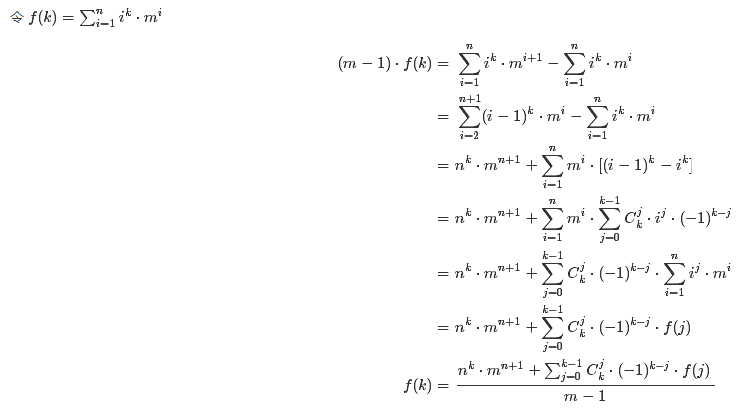
就可以做到O(m²)了。

#include<iostream> 
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
    int x=0,f=1;char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
    while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return x*f;
}
#define N 2010
#define P 1000000007
int n,m,C[N][N],f[N];
int ksm(int a,int k)
{
    if (k==0) return 1;
    int tmp=ksm(a,k>>1);
    if (k&1) return 1ll*tmp*tmp%P*a%P;
    else return 1ll*tmp*tmp%P;
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj3157.in","r",stdin);
    freopen("bzoj3157.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    n=read(),m=read();
    C[0][0]=1;
    for (int i=1;i<=m;i++)
    {
        C[i][0]=C[i][i]=1;
        for (int j=1;j<i;j++)
        C[i][j]=(C[i-1][j-1]+C[i-1][j])%P;
    }
    if (m==1) {cout<<(1ll*n*(n+1)>>1)%P;return 0;}
    f[0]=1ll*m*(ksm(m,n)-1)%P*ksm(m-1,P-2)%P;
    for (int i=1;i<=m;i++)
    {
        f[i]=1ll*ksm(n,i)*ksm(m,n+1)%P;
        for (int j=0;j<i;j++)
        if (i-j&1) f[i]=(f[i]-1ll*C[i][j]*f[j]%P+P)%P;
        else f[i]=(f[i]+1ll*C[i][j]*f[j]%P)%P;
        f[i]=1ll*f[i]*ksm(m-1,P-2)%P;
    }
    cout<<f[m];
    return 0;
}

　　甚至可以做到O(m)。不觉得能看懂了。