Luogu2257 YY的GCD/BZOJ2818 Gcd加强版（莫比乌斯反演+线性筛）

　　一通套路之后得到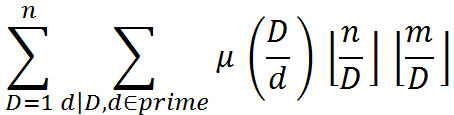

　　求出中间那个函数的前缀和的话就可以整除分块了。

　　暴力求的话复杂度其实很优秀了，大约在n~nlogn之间。

　　不过可以线性筛做到严格线性。考虑其最小质因子，如果是平方因子那么只有其有贡献，否则由于多了一个质因子，将函数值取反并加上该质因子贡献。

#include<iostream> 
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
    int x=0,f=1;char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
    while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return x*f;
}
#define N 10000010
int T,n,m,prime[N],mobius[N],sum[N],cnt=0;
bool flag[N];
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj2818.in","r",stdin);
    freopen("bzoj2818.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    //T=read();
    flag[1]=1;mobius[1]=1;
    for (int i=2;i<=N-10;i++)
    {
        if (!flag[i]) prime[++cnt]=i,mobius[i]=-1,sum[i]=1;
        for (int j=1;j<=cnt&&prime[j]*i<=N-10;j++)
        {
            flag[prime[j]*i]=1;
            if (i%prime[j]==0) {sum[prime[j]*i]=mobius[i];break;}
            else sum[prime[j]*i]=mobius[i]-sum[i],mobius[prime[j]*i]=-mobius[i];
        }
    }
    for (int i=2;i<=N-10;i++) sum[i]+=sum[i-1];
    //while (T--)
    //{
        n=read();//m=read();
        long long ans=0;
        for (int i=1;i<=n;i++)
        {
            int t=n/(n/i);
            ans+=1ll*(sum[t]-sum[i-1])*(n/i)*(n/i);
            i=t;
        }
        /*for (int i=1;i<=min(n,m);i++)
        {
            int t=min(n/(n/i),m/(m/i));
            ans+=1ll*(sum[t]-sum[i-1])*(n/i)*(m/i);
            i=t;
        }*/
        printf(LL,ans);
    //}
    return 0;
}