BZOJ2671 Calc(莫比乌斯反演)
两个多月之前写的题,今天因为看到一道非常相似的题就翻出来了,发现完全不会,没救。
感觉这个题其实第一步是最难想到的,也是最重要的。
设d=gcd(a,b)。那么a=yd,b=xd,且gcd(x,y)=1。a+b|ab等价于x+y|xyd。
由gcd(x,y)=1,得gcd(x+y,y)=gcd(x,x+y)=1。x和y都与x+y互质,那么他们的积xy也与x+y互质,即gcd(xy,x+y)=1。
gcd(xy,x+y)=1,而x+y|xyd,所以x+y|d。
那么现在要求的是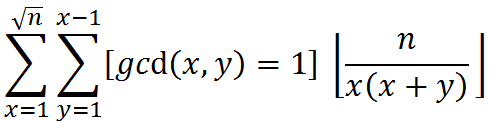
下取整的那部分是满足x+y|d且xd<=n的d的个数。
显然x>√n之后就没有贡献了。这样复杂度变为线性(不算gcd复杂度的话),但还不够。
看到那个gcd=1,妥妥的上莫比乌斯反演。接下来比较套路。

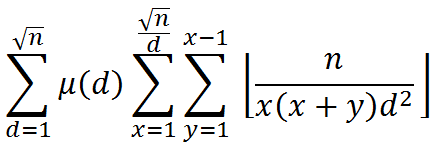
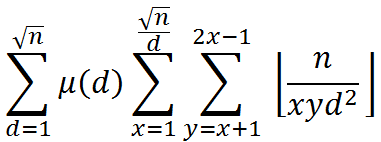
后面一部分的计算可以整除分块。
那这样的时间复杂度是多少呢?看起来是低于线性的,但具体是多少我也不知道……总之他跑的比香港记者还非常快。
今天看到的那道题多了一个限制,即ab/(a+b)与gcd(a,b)互质。
设c=ab/(a+b),那么有(x+y)c=xyd。设d=k(x+y),c=kxy。由gcd(d,c)=1,如果能证明k是正整数的话,那么显然k=1。下证k为正整数。
反证。假设k=u/v(u,v∈N*,gcd(u,v)=1,v>1)。因为c,d均为正整数,所以v|x+y,v|xy。而又有gcd(x+y,xy)=1,矛盾。所以k为正整数。
剩下部分就类似了,由于确定了k=1即d=x+y,可以做到严格的√nlogn。
#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #include<algorithm> using namespace std; #define N 100000 #define min(a,b) ((a)<(b)?(a):(b)) #define ri register int int n,m,mobius[N],prime[N],cnt=0; long long ans=0; bool flag[N]; int main() { cin>>n; m=sqrt(n); flag[1]=1;mobius[1]=1; for (int i=2;i<=m;i++) { if (!flag[i]) prime[++cnt]=i,mobius[i]=-1; for (int j=1;j<=cnt&&prime[j]*i<=m;j++) { flag[prime[j]*i]=1; if (i%prime[j]==0) break; else mobius[prime[j]*i]=-mobius[i]; } } for (ri i=1;i<=m;i++) if (mobius[i]) { ri v=i*i,c=m/i+1; for (ri k=2;k<c;k++) { ri t=n/(k*v),u=(k<<1)-1,h=min(t,u)+1; for (ri j=k+1;j<h;) { ri w=t/j,l=min(u,t/w)+1; ans+=1ll*(l-j)*mobius[i]*w; j=l; } } } cout<<ans; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号