靶形数独

洛谷原题链接

靶形数独这道题是一道很经典的搜索题目，有很多的解题方法，但是Dancing-links这中高端操作身为蒟蒻的我……

我就发一个非常容易理解的题解，你就会发现原来蓝题并不难

先说一下解题思路：

做这道题你首先要知道数独是什么，对吧……要不然没法做了（不知道的戳这里）

然后我们来看一下题目中的棋盘：

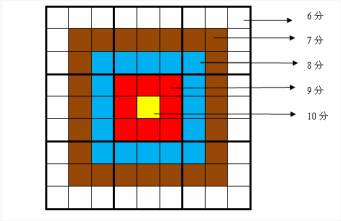
这个棋盘是9*9的，分成了9个宫格，那么我们根据数独的规则，很容易就想到可以用三个数组来记录每行、每列、每个宫格的状态信息，也就是有那些数字已经被放过了。

根据我们手玩数独的经验，我们每做一个新的数独，肯定是先把容易确定的点先填好，在去填其他的。我们就可以这样去搜索，会减少搜索的时间，因为上面的层数扩展的越少，那整个搜索扩展的就会越少，耗时也会少。这里我们就从需要填数最少的一行开始搜索。预处理的时候，用一个结构体记录每一行的行号和空格子的个数，从小到大排序。然后我们可以按照排序的顺序处理出每个需要填数的格子的信息，这样的话搜索的时候就会按照从扩展少的格子开始搜索，节省时间。我的代码里是用em[][]来表示的空格信息。em[i][0/1/2/3]分别表示第i个需要填数的格子所在的行、列、宫格和这个格子的分值。预处理完成之后，就可以dfs了。

这里的dfs就是板子，不过多解释了。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
struct NEED{int row,cnt;}need[10];
int ans=-1,chess[10][10],have,em[100][10],tot;
bool row[10][10],lis[10][10],check[10][10]; //行、列、宫格
int point(int,int);
int askch(int,int);
void dfs(int,int);
bool cmp(NEED,NEED);
int main(){
    register int i,j;
    for(i=1;i<=9;++i)
        for(j=1;j<=9;++j){
            cin>>chess[i][j];
            row[i][chess[i][j]] = lis[j][chess[i][j]] = check[askch(i,j)][chess[i][j]]=1;
            if(!chess[i][j]) need[i].row=i,++need[i].cnt;
            else have+=point(i,j)*chess[i][j];
        }
    sort(need+1,need+10,cmp);
    for(i=1;i<=9;++i)
      for(j=1;j<=9;++j)
        if(!chess[need[i].row][j])
          em[++tot][0]=need[i].row,em[tot][1]=j,em[tot][2]=askch(need[i].row,j),em[tot][3]=point(need[i].row,j);
    dfs(1,have);
    cout<<ans;
    return 0;
}
void dfs(int step,int score){
    if(step==tot+1){
        ans=ans<score ? score : ans;
        return;
    }
    for(int i=1;i<=9;++i)
      if(!row[em[step][0]][i] && !lis[em[step][1]][i] && !check[em[step][2]][i]){
          row[em[step][0]][i]=lis[em[step][1]][i]=check[em[step][2]][i]=1;
          dfs(step+1,score+i*em[step][3]);
          row[em[step][0]][i]=lis[em[step][1]][i]=check[em[step][2]][i]=0;
      }
}
int askch(int i,int j){
    if(i>=1 && i<=3){
        if(j>=1 && j<=3) return 1;
        if(j>=4 && j<=6) return 2;
        return 3;
    }
    if(i>=4 && i<=6){
        if(j>=1 && j<=3) return 4;
        if(j>=4 && j<=6) return 5;
        return 6;
    }
    if(j>=1 && j<=3) return 7;
    if(j>=4 && j<=6) return 8;
    return 9;
}
int point(int i,int j){
    if(j==1 || j==9 || i==1 || i==9) return 6;
    if(i==2 || i==8 || j==2 || j==8) return 7;
    if(i==3 || i==7 || j==3 || j==7) return 8;
    if(i==4 || i==6 || j==6 || j==4) return 9;
    if(i==5 || j==5) return 10;
}
bool cmp(NEED x,NEED y){return x.cnt<y.cnt;}